Chào mừng quý phụ huynh và các em học sinh! Dưới đây là bộ bài tập luyện từ và câu dành cho lớp 4, nhằm giúp các em nâng cao kỹ năng ngữ pháp thông qua hệ thống bài tập đa dạng, từ nhận diện từ loại đến thực hành viết câu. Bộ tài liệu này sẽ hỗ trợ các em rất nhiều trong quá trình học tập và chuẩn bị cho các kỳ thi.
Bộ bài tập luyện từ và câu số 1
Bài 1:
Điền vào chỗ trống để hoàn thiện các ghi chú về danh từ.
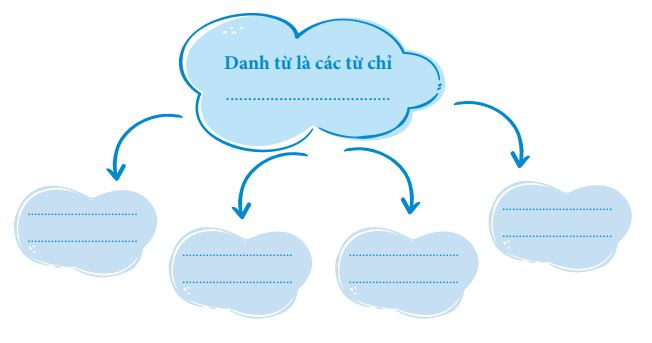 Bài 1 – Bộ bài tập luyện từ và câu số 1
Bài 1 – Bộ bài tập luyện từ và câu số 1
Bài 2:
Ở mỗi nhóm, em hãy viết thêm 5 ví dụ về danh từ.
a. Danh từ chỉ hiện tượng: ………
b. Danh từ chỉ thời gian: ………
Bài 3:
Gạch dưới các danh từ trong mỗi câu sau:
a. Trong lúc Minh bấm máy, nắng nọt từng dòng chữ trên trang vở thì hai cái cùi chữ đánh cộp làm chữ nhảy chồm lên, rất khẳng định dòng.
b. Thi Ca nhìn đường trắng, gương mặt thoáng buồn. Đường ranh giới cứ tồn tại trên mặt bàn hết một tuần.
Bài 4:
Tìm 3 danh từ (có 2 tiếng), trong mỗi từ đều có tiếng “biển”. Đặt câu với 1 trong các danh từ vừa tìm được:
– ………
– ………
Bộ bài tập luyện từ và câu số 2
Bài 1:
Bài đọc trên sử dụng những dấu câu nào?
………
Bài 2:
Dấu hai chấm trong bài có tác dụng gì?
A. Báo hiệu bộ phận câu đằng sau nó là lời của nhân vật.
B. Đánh dấu phần chú thích trong câu.
C. Báo hiệu bộ phận câu đằng sau nó là lời giải thích cho bộ phận đứng trước.
Bài 3:
Tìm các danh từ, động từ có trong câu văn sau:
Sân trại dùng gai làm vũ khí chống lại kẻ thù và khi ấy sân trại che chở luôn cho cả tố chim nữ.
a. Danh từ: ………
b. Động từ: ………
Bài 4:
Thành ngữ nào sau đây nêu đúng ý nghĩa của câu chuyện?
A. Kiến tha lâu cũng đầy tổ.
B. Ăn đến nghĩa trả.
C. Mèo giấu hóa cáo.
Bài 5:
Thêm hình ảnh so sánh vào các câu văn sau:
a. Giọt sương đọng trên lá long lanh như……
b. Cây phượng nở hoa đỏ rực trông như……
c. Dòng sông như……
Tải file bài tập dưới dạng PDF miễn phí tại đây!
Bộ bài tập luyện từ và câu số 3
Bài 1:
Gạch chân dưới các động từ, khoanh tròn vào các danh từ có trong đoạn văn sau:
Cậu bé vừa miệt mài tập luyện, cứ hằng ngày và sau nhiều năm, công lao khó nhọc của cậu đã được tăng thưởng. Gian Pa đó giàu xki trẫ thành một trong những nghệ sĩ dương cầm danh nhất thời bấy giờ.
Bài 2:
Tìm trong bài đọc sau 3 danh từ riêng và ghi lại:
NÓI LỜI CẢI VỪN
Một cậu bé người Ba Lan muốn học đàn dương cảm, thế nhưng cha cậu lại bảo mấy ngón tay của cậu mập mỉm và ngắn quá, không thể nào chơi đàn hay được. Ông khuyên cậu hãy thử học chơi kèn, thế rồi sau đó một nhạc công chuyên nghiệp lại nói rằng cậu không có đủ đòi mô thích hợp.
Một ngày kia, cậu được gặp gỡ nhạc sĩ dương cầm An-tôn Ru-bin-xtên. Con người nổi tiếng này đã trao cho cậu một lời khích lệ mà trước đây cậu chưa từng được nghe: “Này chú bé, chú có thể chơi piano được đấy! Ta nghĩ là chú có thể chơi được… nếu như chú chịu khó luyện tập 7 tiếng mỗi ngày.”
Ôi chao, đó mới thật sự là nguồn cổ vũ lớn lao mà cậu cần đến. Ru-bin-xtên vì đại đã bảo là cậu có thể chơi đàn được! Cậu sẽ phải bỏ ra rất nhiều thời gian để luyện tập nếu muốn chơi đàn đấy, nhưng mà cậu có thể chơi được! Thậm chí còn có thể chơi giỏi! An-tôn Ru-bin-xtên đã nói như vậy mà!
Cậu bé vừa miệt mài tập luyện, cậu càng ra nhiều giải thưởng mỗi ngày và sau nhiều năm, công lao khó nhọc của cậu đã được tăng thưởng: Gian Pa-đờ-riêng-xki trở thành một trong những nghệ sĩ dương cầm danh nhất thời bấy giờ. Một lời động viên đơn giản đã mang đến ngọn lửa đam mê trong lòng một cậu bé, ngọn lửa ấy vẫn cháy sáng mãi trong nhiều năm trôi.
Hãy nhớ rằng những lời động viên mà bạn đang trao gửi hôm nay đôi khi làm thay đổi được mãi mãi một cuộc đời của người đã đón nhận nó.
(Theo Thu Hằng)
Bài 3:
Tìm từ có nghĩa giống với mỗi từ dưới đây và đặt câu với mỗi từ vừa tìm được.
– lo lắng: ………
– thì thào: ………
– ngạo mạn: ………
– xao nhãng: ………
Bài 4:
Gạch dưới tên các cơ quan tổ chức/danh từ riêng chưa viết hoa đúng quy tắc và sửa lại cho đúng.
NGÔI TRƯỜNG NẰM Ở ĐẦU NGUỒN SÔNG
Trường tiểu học Sinh tồn nằm giữa những hàng cây phong ba, cây bàng vuông xanh thẫm trên đảo Sinh Tồn đầy nắng gió. Hằng năm, trường đều nhận được sự quan tâm, hỗ trợ của ủy ban nhân dân xã Sinh Tồn, Câu lạc bộ Vì Hoàng sa – Trường sa thân yêu,… ở nơi đầu ngọn sóng, các bạn nhỏ ngày một trưởng thành và thêm yêu biển đảo quê hương.
(Theo Phan Phùng Duy)
Sửa lại:
………
Bộ bài tập luyện từ và câu số 4
Bài 1:
Dấu “hai chấm” trong bài đọc dưới đây có tác dụng gì?
MÃI RÌU
Ngày xưa ngày xưa, có một tiều phu khỏe mạnh đến tìm gặp ông chủ xưởng gỗ để tìm việc làm và anh được nhận vào làm một công việc phù hợp với khả năng: đốn gỗ. Tiền lương được trả thật sự cao và điều kiện làm việc rất tốt. Chính vì lý do đó mà người tiều phu đã làm việc hết sức mình. Ông chủ đưa cho anh một cái rìu và chỉ anh nơi để đốn gỗ. Ngày đầu tiên, người tiều phu mang về 18 cây.
– Thật tuyệt vời, hãy tiếp tục như thế! – Ông chủ khích lệ.
Nghe những lời khuyến khích của ông chủ, người tiều phu gắng sức làm việc trong ngày tiếp theo nhưng anh ta chỉ mang về được 15 cây. Ngày thứ ba anh cố gắng làm việc hơn nữa nhưng cũng chỉ mang về được 10 cây. Những ngày tiếp theo số cây anh mang về ngày càng ít hơn.
“Tôi đã đánh mất sức mạnh của mình” – người tiều phu nghĩ vậy. Anh tìm đến ông chủ để nó lãi xin lỗi và giải thích rằng anh không hiểu tại sao lại như thế.
Lần cuối cùng anh mời cái rìu của anh là vào khi nào? – Ông chủ hỏi.
Mãi rìu ư? Tôi không có thời gian để mài nó. Tôi đã rất bận trong việc gắng sức đến những cái cây này.
(Sưu tầm)
Bài 2:
Gạch chân các từ không cùng nhóm nghĩa trong mỗi chuỗi từ dưới đây.
A. trung bình, trung du, trung điểm, trung hiếu, trung thu
B. trung thành, trung thực, trung nghĩa, trung tâm, trung kiên
C. thật thà, thành thật, thành khẩn, khẩn thiết, chân thật
D. giả dối, gian dối, gian tà, bội rối, giả tạo, dối trá, lừa dối
Bài 3:
a. Gạch chân từ viết sai quy tắc chính tả trong đoạn thơ rồi viết lại cho đúng.
Hà nội có hồ Gươm
Nước xanh như pha mực
Bên hồ ngàn tháp bút
Viết thơ lên trời cao
Những năm Giáp bát phá
Ba đỉnh vẫn xanh cây
Trăng và ngựa chứa một cốt
Phủ tây hồ hoa bay
(Hà Nội, Trần Đăng Khoa)
b. Tìm và ghi lại các danh từ chung trong đoạn thơ trên.
………
Bộ bài tập luyện từ và câu số 5
CẢNH KIẾN ĐẾN CẢNH
Trong khu rừng nọ, một đàn kiến bắt chẹt gặp nguy hiểm: sa vào vùng nước. Một chú chim nhảy bay ra khỏi tổ trên cành cây gần bên thấy động lòng thương, chú bay vút ra nhất mấy cành rác thả xuống làm cầu cho đàn kiến thoát.
Ngày tháng trôi qua, chú chim ấy cũng không còn nhờ đến đàn kiến nọ nữa. Chú thuộc loại chim nhảy rất thích làm tổ trên cành sần bời vì cành cây tua tủa đầy gai nhọn hoạt. Sân trại dùng gai làm vũ khí chống kẻ thù và khi ấy sân trại che chở luôn cho cả tố chim nữ.
Mèo, quá to xác khó mà lên lưới giữa những mũi gai sắc nhọn để đến được tố chim. Nhưng một hôm, con mèo xám bất chấp gai góc cũ tìm cách lặng mò tới gần tố chim nọ. Song cả một đàn kiến dày đặc nhanh chóng tấn công hình ra khắp cành sân có tố chim. Mèo xám hết hoảng bạt chạy ngay bởi vì nó nhỡ có đàn kiến lẫn vào tai đột đầu nhói.
Như vậy, đàn kiến bị sa vào vùng nước ngày ấy đã quên ơn chú chim đã làm cầu cho đàn kiến thoát.
(Nguồn Internet)
Bài 1:
Bài đọc trên sử dụng những dấu câu nào?
………
Bài 2:
Dấu hai chấm trong bài có tác dụng gì?
A. Báo hiệu bộ phận câu đằng sau nó là lời của nhân vật.
B. Đánh dấu phần chú thích trong câu.
C. Báo hiệu bộ phận câu đằng sau nó là lời giải thích cho bộ phận đứng trước.
Bài 3:
Tìm các danh từ, động từ có trong câu văn sau:
Sân trại dùng gai làm vũ khí chống lại kẻ thù và khi ấy sân trại che chở luôn cho cả tố chim nữ.
a. Danh từ: ………
b. Động từ: ………
Bài 4:
Thành ngữ nào sau đây nêu đúng ý nghĩa của câu chuyện?
A. Kiến tha lâu cũng đầy tổ.
B. Ăn đến nghĩa trả.
C. Mèo giấu hóa cáo.
Bài 5:
Thêm hình ảnh so sánh vào các câu văn sau:
a. Giọt sương đọng trên lá long lanh như……
b. Cây phượng nở hoa đỏ rực trông như……
c. Dòng sông như……
Hy vọng bộ bài tập Luyện từ và câu lớp 4 kết nối tri thức PDF ở trên đã giúp các em học sinh củng cố kiến thức ngữ pháp và rèn luyện kỹ năng sử dụng tiếng Việt một cách hiệu quả, từ đó nâng cao điểm số trong các bài thi và bài kiểm tra trên lớp.
Các bài tập này đều có sẵn trong cuốn Bài tập bổ trợ nâng cao Tiếng Việt lớp 4 và 50 đề tăng điểm nhanh Tiếng Việt lớp 4. Các em hãy mua ngay hai cuốn sách này để học tốt môn tiếng Việt hơn nhé!
Link đến sách Bài tập bổ trợ nâng cao Tiếng Việt lớp 4: https://drive.google.com/file/d/1u2c2D649abdMmUxLvldqSkmjtrmR0U5z/view
Link đến sách 50 đề tăng điểm nhanh Tiếng Việt lớp 4: https://drive.google.com/file/d/1_UY0QJyXiqcUXCkCMSh9HiMcdYhHG3ia/view
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 4 hàng đầu tại Việt Nam.
Tkbooks.vn
 Hình 6 – Bài 6
Hình 6 – Bài 6 Hình 7 – Bài 7
Hình 7 – Bài 7 Hình 9 – Bài 9
Hình 9 – Bài 9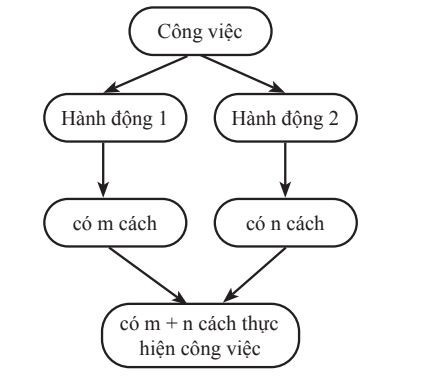
 Ví dụ về quy tắc cộng
Ví dụ về quy tắc cộng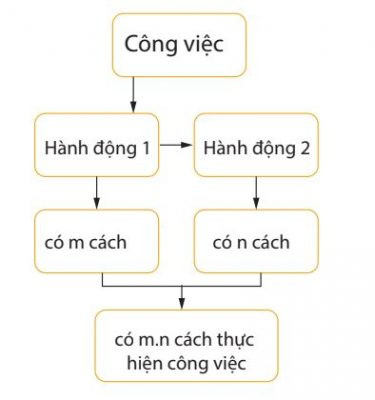 Quy tắc nhân
Quy tắc nhân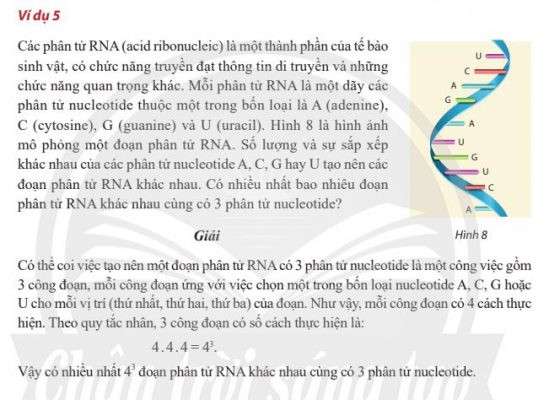 Ví dụ về quy tắc nhân
Ví dụ về quy tắc nhân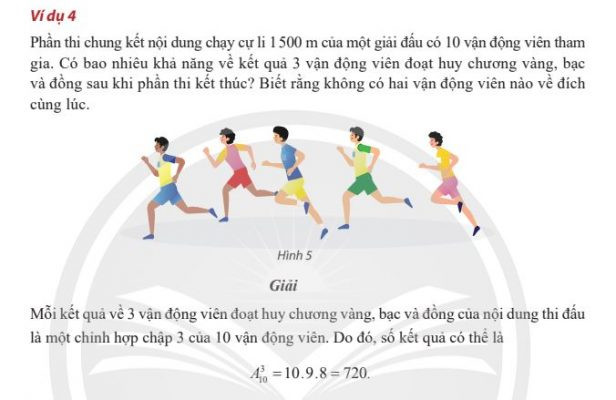 Ví dụ về chỉnh hợp
Ví dụ về chỉnh hợp Ví dụ về tổ hợp
Ví dụ về tổ hợp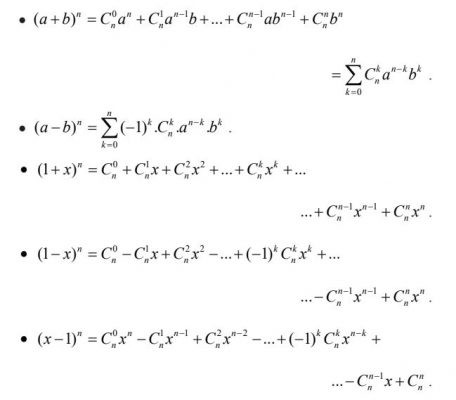 Nhị thức Newton
Nhị thức Newton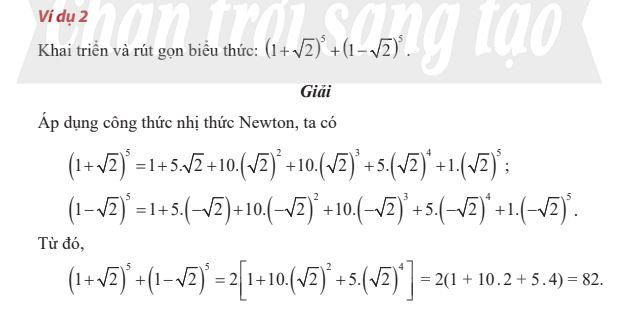 Ví dụ về nhị thức Newton
Ví dụ về nhị thức Newton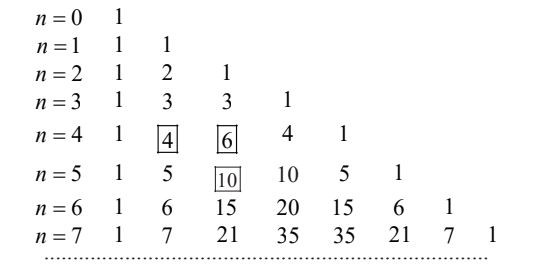 Tam giác Pascal
Tam giác Pascal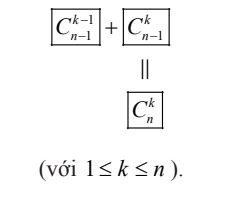 Hàng dọc thức Pascal
Hàng dọc thức Pascal Cách tính tổ hợp bằng máy tính cầm tay
Cách tính tổ hợp bằng máy tính cầm tay Bài tập về tổ hợp, chỉnh hợp
Bài tập về tổ hợp, chỉnh hợp Bài tập về nhị thức Newton
Bài tập về nhị thức Newton
 Bài tập Unit 1 – File 1
Bài tập Unit 1 – File 1 File 2
File 2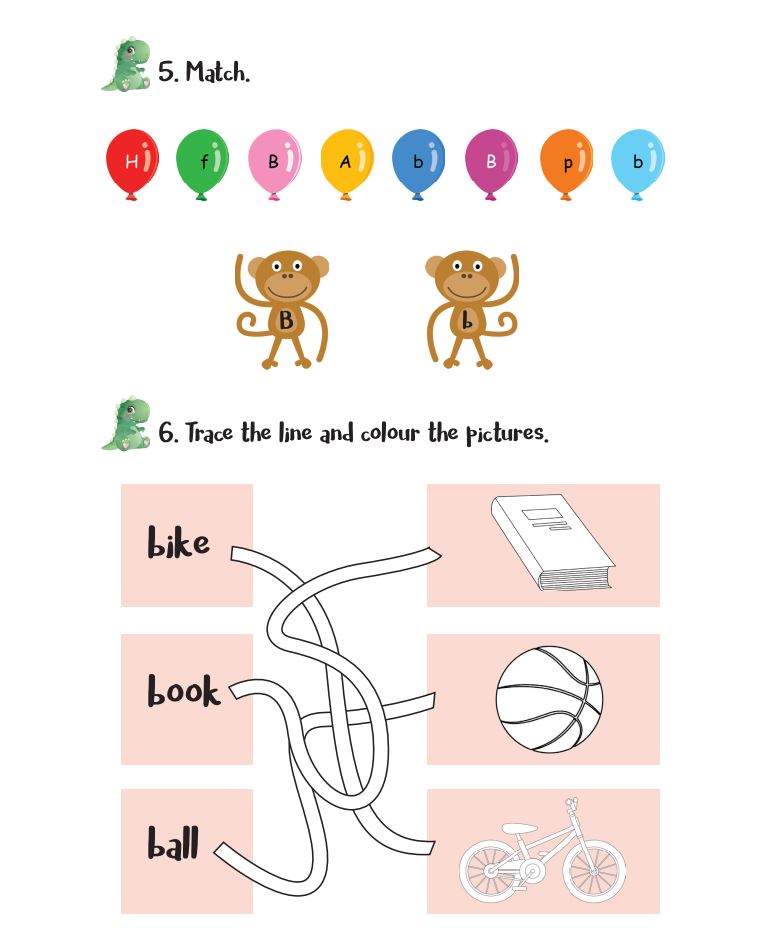 File 3
File 3 File 4
File 4 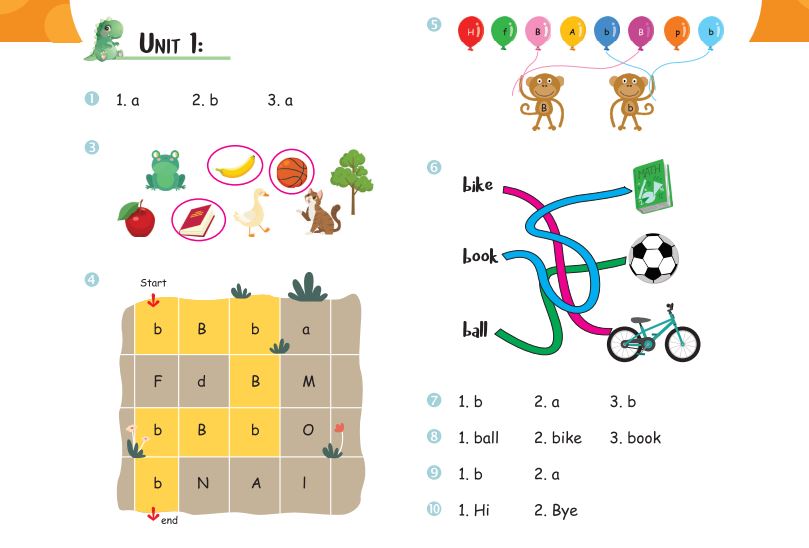 Đáp án bài tập tiếng Anh Unit 1
Đáp án bài tập tiếng Anh Unit 1
 Gặp gỡ giữa các nhà xuất bản
Gặp gỡ giữa các nhà xuất bản
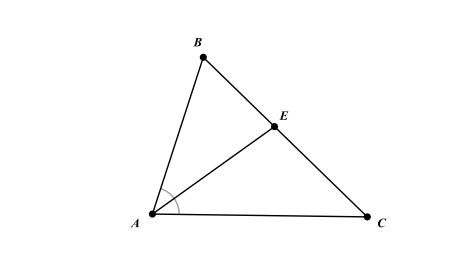 Đường phân giác của tam giác
Đường phân giác của tam giác
 Nội Dung Sách Giới Tư Duy Toán Học
Nội Dung Sách Giới Tư Duy Toán Học Bố Mẹ Học Cùng Sách Giới Tư Duy Toán Học
Bố Mẹ Học Cùng Sách Giới Tư Duy Toán Học
 Tác giả Mai Phương chia sẻ bí quyết tăng từ 3 đến 4 điểm trong hai tháng ôn thi.
Tác giả Mai Phương chia sẻ bí quyết tăng từ 3 đến 4 điểm trong hai tháng ôn thi. Hướng dẫn giải chi tiết trong các cuốn sách luyện đề.
Hướng dẫn giải chi tiết trong các cuốn sách luyện đề. Chia sẻ của độc giả
Chia sẻ của độc giả
 Hình ảnh bài tập tự luận 1
Hình ảnh bài tập tự luận 1 Hình ảnh bài tập khó
Hình ảnh bài tập khó
 Ví dụ về dãy số tăng, dãy số giảm
Ví dụ về dãy số tăng, dãy số giảm Ví dụ về cấp số cộng
Ví dụ về cấp số cộng Bài tập ví dụ cơ bản về cấp số cộng
Bài tập ví dụ cơ bản về cấp số cộng Ví dụ về cấp số nhân
Ví dụ về cấp số nhân Bài tập về dãy số
Bài tập về dãy số Bài tập về cấp số cộng
Bài tập về cấp số cộng Bài tập về cấp số nhân
Bài tập về cấp số nhân