Bài soạn văn Quang Trung đại phá quân Thanh lớp 8 ngắn nhất dưới đây sẽ giúp các em học sinh hiểu rõ hơn về tinh thần yêu nước, lòng dũng cảm và tài trí lãnh đạo của Vua Quang Trung trong cuộc chiến chống quân xâm lược.
I. Khái quát về tác giả Ngô Gia Văn Phái và tác phẩm Quang Trung đại phá quân Thanh
1. Tác giả Ngô Gia Văn Phái
Ngô Gia Văn Phái là nhóm tác giả thuộc dòng họ Ngô Thì ở làng Tảo Thanh Oai, Hà Nội ngày nay. Đây là dòng họ có truyền thống văn chương với những tên tuổi tiêu biểu như: Ngô Thì Ỉch (1709 – 1736), Ngô Thì Sĩ (1726 – 1780); Ngô Thì Nhậm (1746 – 1803), Ngô Thì Chí (1753 – 1788), Ngô Thì Du (1772 – 1840),…
 Hình ảnh tác giả Ngô Thì Chí
Hình ảnh tác giả Ngô Thì Chí
2. Văn bản Quang Trung đại phá quân Thanh
Giới thiệu tác phẩm Quang Trung đại phá quân Thanh
“Hoàng Lê nhất thống chí” là cuốn tiểu thuyết lịch sử gồm 17 hồi, viết bằng chữ Hán, phản ánh bức tranh rộng lớn của xã hội Việt Nam từ cuối thế kỷ XVIII đến đầu thế kỷ XIX với nhiều câu chuyện và nhân vật lịch sử có thật. Tác phẩm phản ánh thực trạng thời đại dân tộc đang bị áp bức dưới tập đoàn phong kiến Lê – Trịnh, đồng thời ca ngợi cuộc khởi nghĩa Tây Sơn do người anh hùng áo vải Nguyễn Huệ lãnh đạo.
Văn bản “Quang Trung đại phá quân Thanh” thuộc hồi thứ XIV của tác phẩm, kể về cuộc hành quân thần tốc và chiến thắng lẫy lừng của nghĩa quân Tây Sơn, đồng thời phản ánh sự thất bại thảm hại của vua tôi nhà Lê sau khi quân Thanh thua trận.
 Văn bản “Quang Trung đại phá quân Thanh” thuộc hồi thứ XIV của tác phẩm
Văn bản “Quang Trung đại phá quân Thanh” thuộc hồi thứ XIV của tác phẩm
Tóm tắt văn bản Quang Trung đại phá quân Thanh
Khi nghe tin quân Thanh kéo vào Thăng Long, Nguyễn Huệ đang ở Phú Xuân đã lên ngôi hoàng đế, lấy hiệu là Quang Trung và chuẩn bị kéo quân ra Bắc. Đến Nghệ An, vua tuyển thêm binh lính, mở một cuộc duyệt binh lớn và ra lệnh phất cờ tập trung quân dân, chống giặc.
Ngày 30 Tết, đại quân đến Tam Điệp, vua cho quân sĩ ăn Tết trước để tiến vào Thăng Long. Đêm mùng 3 tháng Giêng, chiến thắng Hạ Hồi. Ngày mùng 5, ta đánh thắng trận Ngọc Hồi, quân Thanh đại bại. Trưa cùng ngày, Quang Trung tiến binh vào thành Thăng Long; Tôn Sĩ Nghĩa bỏ chạy, quân Thanh chết như ngả rạ; vua tôi nhà Lê cũng nháo nhác bỏ chạy theo giác vệ phương Bắc.
II. Đặc điểm của truyện lịch sử trong văn bản Quang Trung đại phá quân Thanh
1. Bối cảnh lịch sử:
-
Tác phẩm “Hoàng Lê nhất thống chí” lấy bối cảnh là cuộc kháng chiến chống quân Thanh xâm lược của nghĩa quân Tây Sơn năm 1789.
-
Đoạn trích “Quang Trung đại phá quân Thanh” tái hiện lại quá trình người anh hùng áo vải Nguyễn Huệ lên ngôi hoàng đế, cầm quân ra Bắc tiêu diệt quân Thanh và bẽ bàng tay sai bán nước ở Thăng Long.
2. Nhân vật:
-
Truyện có nhiều nhân vật có thật trong lịch sử: vua Quang Trung – Nguyễn Huệ, Ngô Văn Sĩ, Nguyễn Văn Tuyết, Ngô Thì Nhậm, Nguyễn Thiệp, vua Lê Chiêu Thống, Tôn Sĩ Nghĩa, Sầm Nghi Đống.
-
Nhân vật chính là vua Quang Trung – nhân vật lịch sử có thật và có ảnh hưởng lớn đối với sự phát triển của lịch sử Việt Nam giai đoạn cuối thế kỷ XVIII. Nhân vật được xây dựng thông qua lời nói, hành động, cách ứng xử với các nhân vật khác.
3. Ngôn ngữ:
-
Ngôn ngữ được sử dụng trong tác phẩm mang đậm sắc thái cổ.
-
Cách xưng hô, việc sử dụng các câu văn biến ngữ góp phần tái hiện không gian của thời kỳ lịch sử mà tác phẩm phản ánh.
4. Chi tiết tiêu biểu:
-
Chi tiết vua Quang Trung ban lệnh phất cờ cho binh sĩ trong cuộc duyệt binh lớn ở Nghệ An cho thấy trí tuệ sáng suốt, nhạy bén của ông.
-
Chi tiết “… vua Quang Trung cười với địch thục, mở sáng ngày mùng 5 tiến sát đến Ngọc Hồi” là nổi bật hình ảnh một vị vua – một vị tướng tài năng, dũng mãnh khi xung trận, trực tiếp đốc thúc binh sĩ giành những chiến thắng quan trọng, đánh đuổi quân thù ra khỏi bờ cõi.
2. Đọc hiểu văn bản Quang Trung đại phá quân Thanh
2.1. Hình tượng người anh hùng Quang Trung – Nguyễn Huệ
– Quang Trung là một vị vua có nhiều phẩm chất cao đẹp.
- Quyết đoán, hành động nhanh chóng, có chủ đích.
– Ngày 24/11/1788, khi nghe tin cấp báo, Nguyễn Huệ khi đó ở Phú Xuân gấp rút liên hợp tướng sĩ định thân chinh cầm quân đi ngay.
– Nghe lời khuyên của những người đến giúp, ngày 25 tháng chạp, ông làm lễ cáo trời đất, lên ngôi hoàng đế, lấy niên hiệu là Quang Trung, tự mình đốc xuất đại binh cùng ra đi.
Ngày 29 tháng chạp, nghe lời khuyên của Nguyễn Thiệp, ông tuyên mộ binh lính ở Nghệ An, tổ chức buổi duyệt binh lớn và ra lệnh phất cờ tập trung nhắm chống quân Thanh.
– Vua Quang Trung hợp binh với các tướng sĩ lên kế hoạch đối phó với quân Thanh sau chiến thắng.
=> Chỉ trong vòng một tháng, Nguyễn Huệ đã làm được rất nhiều việc lớn. Điều đó cho thấy Nguyễn Huệ là người quyết đoán, có hành động mạnh mẽ, nhanh chóng, có chủ đích.
- Trí tuệ mẫn tiệp, sáng suốt, nhạy bén
– Lời phất cờ đã thể hiện trí tuệ sáng suốt, nhạy bén của vua Quang Trung.
-
Khẳng định chủ quyền của nước Đại Việt.
-
Nếu bắt được tâm của giác Thanh muốn biến nước ta thành quân huyện của chúng.
-
Tự hào về truyền thống đánh giá của cha ông.
-
Tin tưởng vào chính nghĩa và kêu gọi quân sĩ đánh giá.
-
Ra kỉ luật nghiêm khắc với quân sĩ.
=> Lời phất cờ với lời lẽ rõ ràng, nghiêm trang đã khích lệ được tinh thần yêu nước, ý chí quyết tâm đánh giá của binh sĩ.
– Việc xét đoán và dùng người cũng cho thấy trí tuệ sáng suốt, sự điềm đạm và công minh của ông.
-
Đối với các tướng Sĩ, Lân, Nhậm, ông phân tích năng lực của từng người, phân tích đúng sai, khen chê đúng mức.
-
Ông cũng biết lắng nghe lời khuyên, ý kiến của thuộc cấp để đưa ra những quyết định đúng đắn và hợp lý nhất.
=> Nhờ đó, Nguyễn Huệ được tướng sĩ kính trọng và giúp ông đưa ra những quyết định đúng đắn đến kịp thời.
- Có tầm nhìn xa, trông rộng
– Ông có niềm tin sắt đá vào chiến thắng: “Chẳng qua mười ngày có thể đuổi được người Thanh.”
– Ông cũng vạch sẵn kế hoạch ngoại giao với nhà Thanh sau chiến thắng. Đây là một trong những điểm cho thấy tài ngoại giao và tầm nhìn xa, trông rộng của ông.
- Vua Quang Trung luôn chủ động, đoán định chính xác tương lai và đề ra các bước đi hợp lý.
2.2. Sự đối lập giữa quân Tây Sơn và bè lũ bán nước, cướp nước
- Sự đối lập giữa vua Quang Trung và vua Lê
-
Trong khi vua Quang Trung là một vị anh hùng chống ngoạn xâm thì vua Lê lại là kẻ còng rắn gánh – một ông vua bán nước.
-
Vua Quang Trung là người văn võ toàn tài, mưu lược hơn người còn vua Lê Chiêu Thống lại là kẻ bất tài, chỉ biết chạy trốn và khóc lóc khi gặp biến cố.
- Sự đối lập giữa đại quân Tây Sơn và quân Thanh
-
Đại quân của vua Quang Trung được tổ chức quy củ, có trật tự, tiến hành một cuộc hành quân có một không hai trong lịch sử. Trong khi đó, đội quân nhà Thanh lại lạm kiêu binh, hổ hợ.
-
Đội quân Tây Sơn dũng mãnh phi thường, sẵn sàng xả thân để đánh đuổi giặc xâm lược; chủ tướng là vua Quang Trung – văn võ toàn tài, có tầm nhìn xa, trông rộng. Trong khi đó, quân Thanh toàn những kẻ hèn nhát, từ chủ tướng đến binh lính đều chỉ biết bỏ chạy khi phải đối mặt với quân Tây Sơn.
=> Nghệ thuật tương phản đã làm nổi bật những phẩm chất tốt đẹp của người anh hùng áo vải Quang Trung; đồng thời, phải bày tỏ mặt yếu hèn của những kẻ bán nước cướp nước.
III. Tổng kết về văn bản Quang Trung đại phá quân Thanh
1. Nghệ thuật
– Tác giả lựa chọn trình tự kể các sự kiện lịch sử có thật giúp người đọc nắm được các diễn biến chính của sự kiện.
– Nhân vật lịch sử Quang Trung – Nguyễn Huệ được khắc họa bằng ngôn ngữ kể chuyện chân thực, sinh động thông qua lời nói và hành động.
– Gợi cảm khiến cho người đọc cảm nhận được sâu sắc hình ảnh người anh hùng áo vải Quang Trung – Nguyễn Huệ với những chiến công lẫy lừng trước quân đội nhà Thanh.
2. Nội dung
– Bằng cái nhìn khách quan và niềm tự hào dân tộc, các tác giả Hoàng Lê nhất thống chí đã tái hiện hình ảnh người anh hùng áo vải Quang Trung – Nguyễn Huệ với chiến công thần tốc trước quân đội nhà Thanh.
– Qua văn bản, độc giả cũng có thể cảm nhận được không khí hào hùng của dân tộc trong cuộc chiến chống quân xâm lược cuối thế kỷ XVII.
3. Kiến thức bổ sung:
- Viết đoạn văn (khoảng 7 đến 9 câu) nêu cảm nhận về một chi tiết trong văn bản Quang Trung đại phá quân Thanh lớp 8
Trong văn bản “Quang Trung đại phá quân Thanh,” chi tiết Vua Quang Trung kích lệ quân sĩ trước trận chiến để lại cho tôi nhiều ấn tượng sâu sắc. Hình ảnh một vị vua trẻ trung, mạnh mẽ, đứng trước hàng ngàn binh lính, truyền lửa nhiệt huyết và ý chí chiến đấu đã khơi dậy lòng yêu nước và sự quyết tâm của cả quân đội. Lời nói của ông như tiếng chuông vang vọng, khích lệ tinh thần yêu nước, quyết tâm bảo vệ Tổ quốc của mỗi người lính. Chi tiết này không chỉ thể hiện sự thông minh, bản lĩnh của Vua Quang Trung mà còn khẳng định tinh thần kiên cường của dân tộc Việt Nam trước sự xâm lược. Qua đó, tôi cảm nhận rõ hơn về tâm vóc của vị vua vĩ đại, người đã dẫn dắt dân tộc vượt qua những khó khăn, thách thức để giành lấy tự do. Đồng thời, chi tiết này cũng nhắc nhở chúng ta về giá trị của lòng yêu nước và trách nhiệm với Tổ quốc trong cuộc sống hôm nay.
- Viết đoạn văn 7 – 9 câu chứng minh Quang Trung là người có tầm nhìn xa trông rộng
Quang Trung là một vị vua có tầm nhìn xa trông rộng, điều này thể hiện rõ qua những quyết định và hành động chiến lược trong cuộc kháng chiến chống quân Thanh. Trước hết, ông hiểu rõ sức mạnh và điểm yếu của quân đội nhà Thanh, từ đó lập ra kế hoạch tấn công bất ngờ, nhanh chóng khiến quân địch không kịp ứng phó. Ông đã tổ chức một cuộc hành quân thần tốc từ Phú Xuân ra Bắc Hà chỉ trong thời gian ngắn, tạo ra yếu tố bất ngờ cho đối thủ. Hơn nữa, sau khi giành chiến thắng, Quang Trung còn nghĩ đến việc duy trì hòa bình lâu dài bằng cách thiết lập quan hệ ngoại giao với nhà Thanh, tránh những cuộc xung đột trong tương lai. Những hành động này không chỉ thể hiện tài trí của ông mà còn cho thấy sự hiểu biết sâu sắc về lòng dân và sự cần thiết phải bảo vệ độc lập của đất nước. Vì vậy, Quang Trung thực sự xứng đáng trở thành hình mẫu cho những nhà lãnh đạo có tầm nhìn và trách nhiệm với Tổ quốc.
Hy vọng bài soạn văn Quang Trung đại phá quân Thanh lớp 8 ngắn nhất trên đây sẽ giúp các em học sinh nắm bắt được nội dung và ý nghĩa của tác phẩm, từ đó trau dồi kiến thức văn học và lịch sử. Đừng quên tham khảo những bài viết khác để nâng cao kiến thức môn Ngữ văn của mình, các em nhé!
 Hình 3 – Bài 3
Hình 3 – Bài 3 Hình 3 – Bài 3
Hình 3 – Bài 3 Hình 3 – Bài 3
Hình 3 – Bài 3 Hình 6 – Bài 6
Hình 6 – Bài 6 Hình 7 – Bài 7
Hình 7 – Bài 7 Hình 7 – Bài 7
Hình 7 – Bài 7 Hình 9 – Bài 9
Hình 9 – Bài 9 Hình 9 – Bài 9
Hình 9 – Bài 9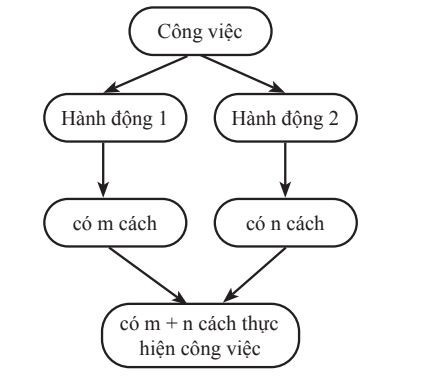
 Ví dụ về quy tắc cộng
Ví dụ về quy tắc cộng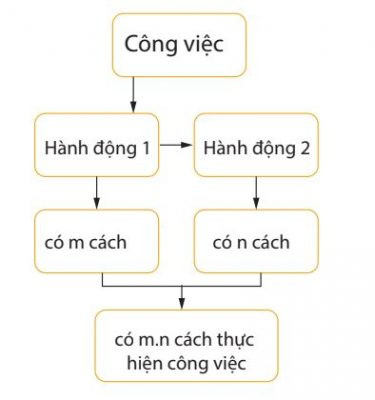 Quy tắc nhân
Quy tắc nhân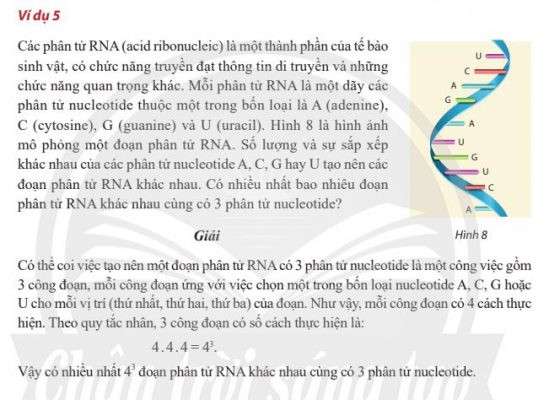 Ví dụ về quy tắc nhân
Ví dụ về quy tắc nhân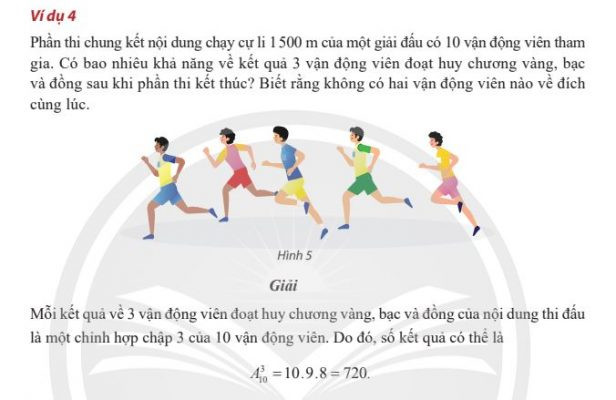 Ví dụ về chỉnh hợp
Ví dụ về chỉnh hợp Ví dụ về tổ hợp
Ví dụ về tổ hợp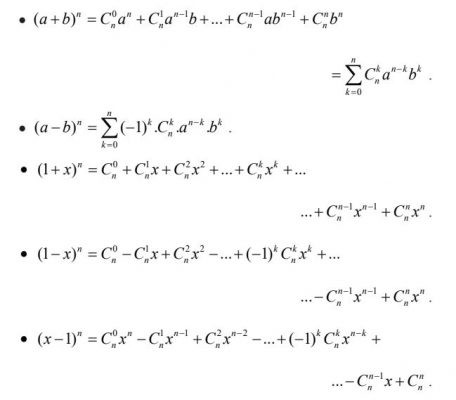 Nhị thức Newton
Nhị thức Newton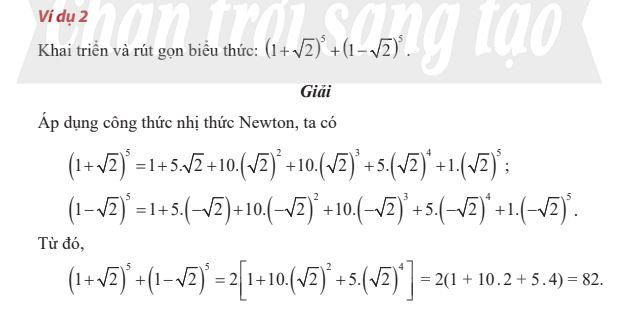 Ví dụ về nhị thức Newton
Ví dụ về nhị thức Newton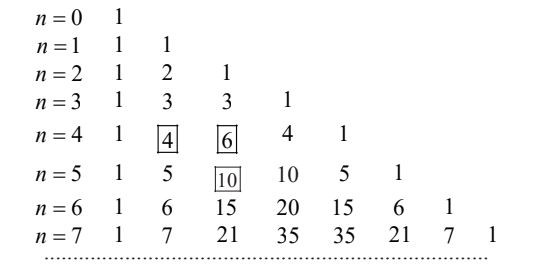 Tam giác Pascal
Tam giác Pascal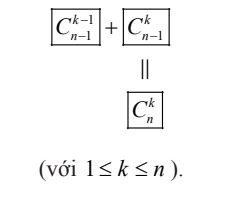 Hàng dọc thức Pascal
Hàng dọc thức Pascal Cách tính tổ hợp bằng máy tính cầm tay
Cách tính tổ hợp bằng máy tính cầm tay Bài tập về tổ hợp, chỉnh hợp
Bài tập về tổ hợp, chỉnh hợp Bài tập về nhị thức Newton
Bài tập về nhị thức Newton
 Hướng dẫn cách làm bài văn nghị luận về vấn đề đọc sách của giới trẻ
Hướng dẫn cách làm bài văn nghị luận về vấn đề đọc sách của giới trẻ

 Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung
Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài
Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài
 Văn bản “Quang Trung đại phá quân Thanh” thuộc hồi thứ XIV của tác phẩm
Văn bản “Quang Trung đại phá quân Thanh” thuộc hồi thứ XIV của tác phẩm
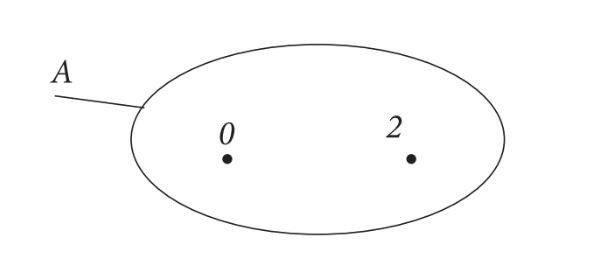 Minh họa một tập hợp cho trước bằng hình vẽ – Ảnh 2
Minh họa một tập hợp cho trước bằng hình vẽ – Ảnh 2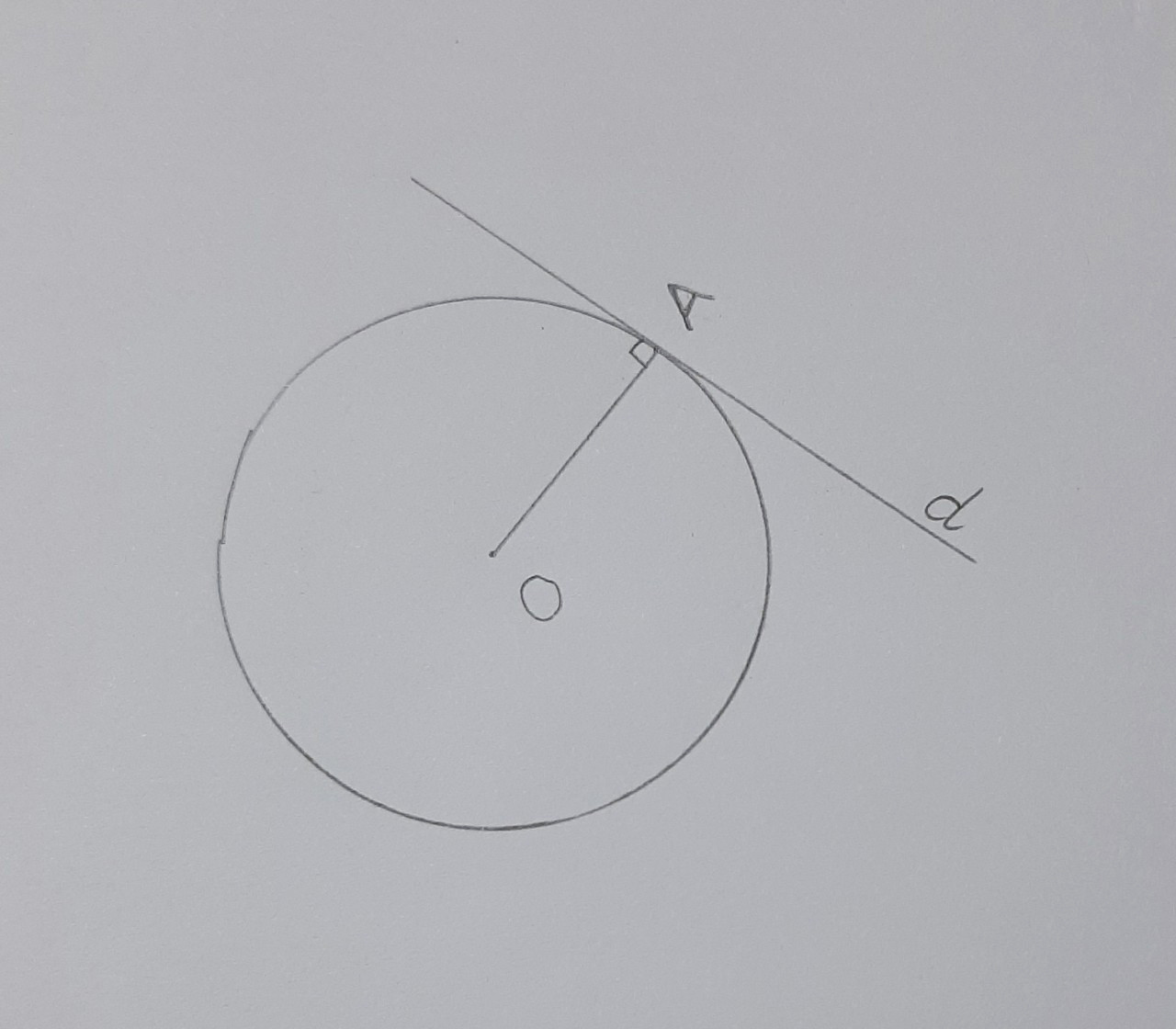
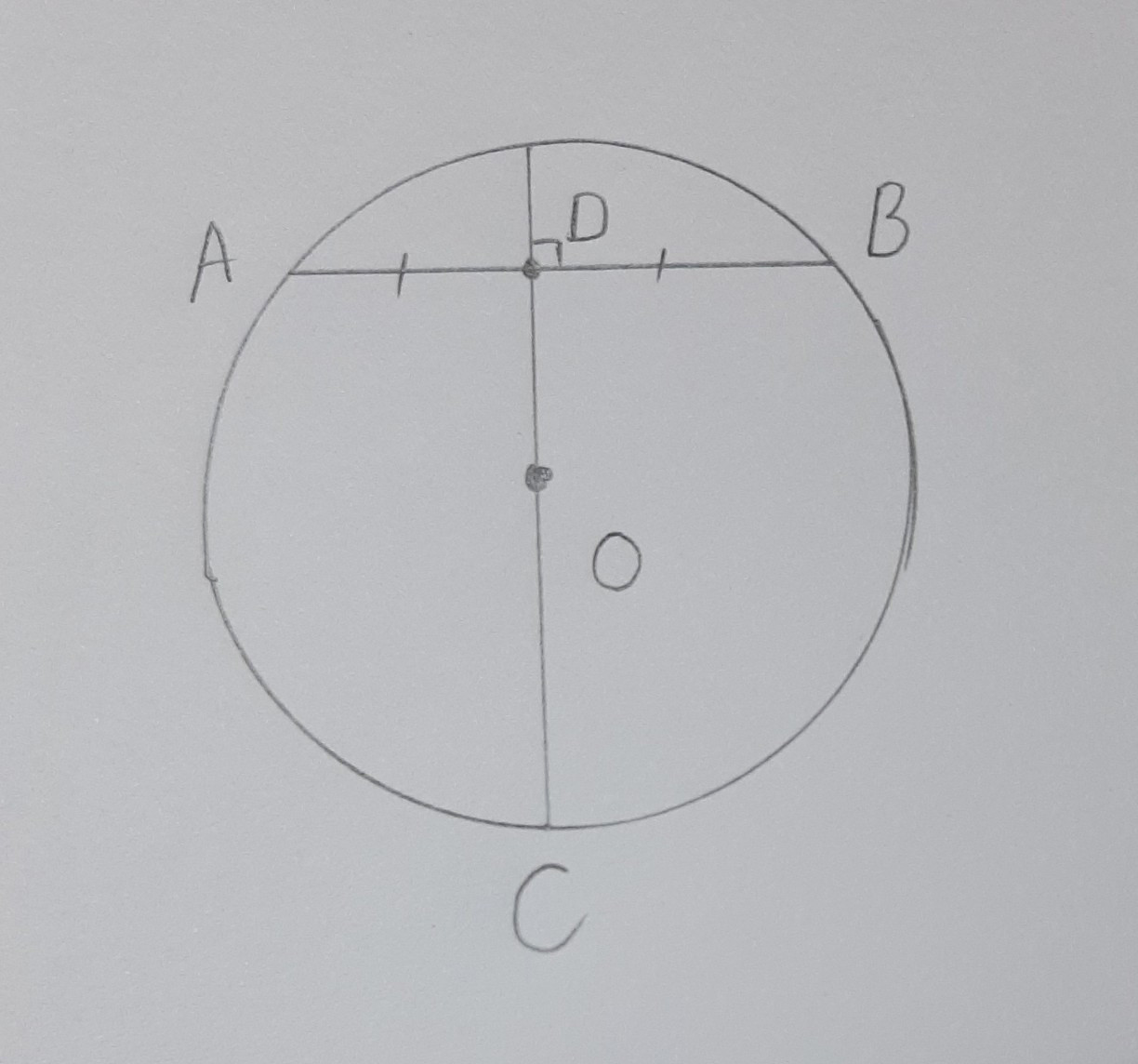 Chứng minh đường kính vuông góc với dây cung của đường tròn
Chứng minh đường kính vuông góc với dây cung của đường tròn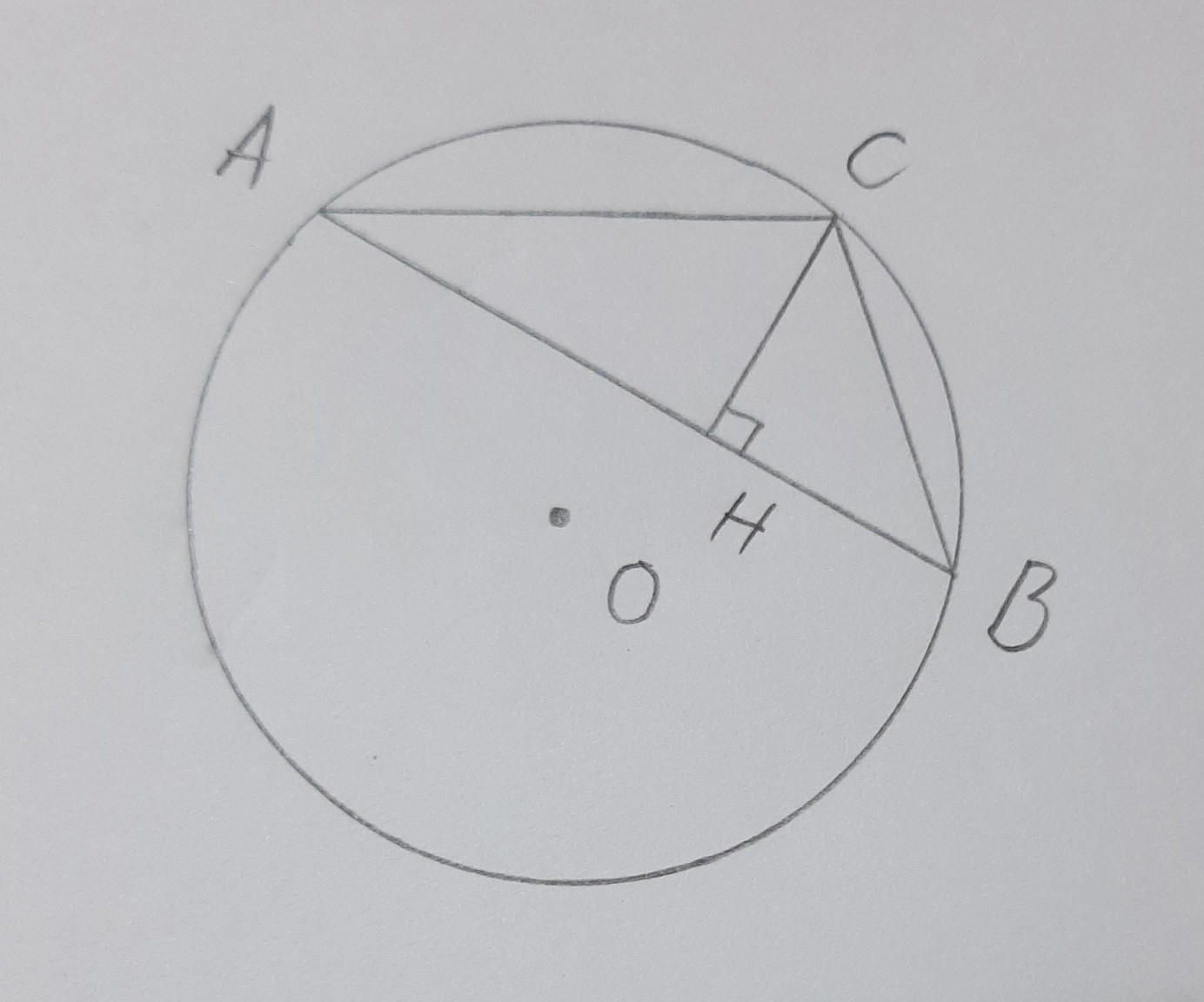 Chứng minh từ góc nội tiếp và góc ở tâm
Chứng minh từ góc nội tiếp và góc ở tâm
