Trong bài viết này, chúng ta sẽ cùng tìm hiểu về tia phân giác và những đặc điểm, tính chất quan trọng của nó trong chương trình Toán lớp 9. Ở đây, chúng ta sẽ khám phá các phương pháp để chứng minh tia phân giác thừa hưởng những kiến thức toán học cần thiết, đồng thời nâng cao khả năng tư duy logic cho học sinh.
I. Khái niệm và Tính chất của Tia Phân Giác
1. Tia Phân Giác của Một Góc
a. Khái niệm Tia Phân Giác
Tia phân giác của một góc là tia nằm giữa hai cạnh và chia góc đó thành hai góc bằng nhau. Trong hình vẽ dưới đây, tia Oy là tia phân giác của góc xOz, với góc ∠xOy = ∠yOz = ½ ∠xOz.
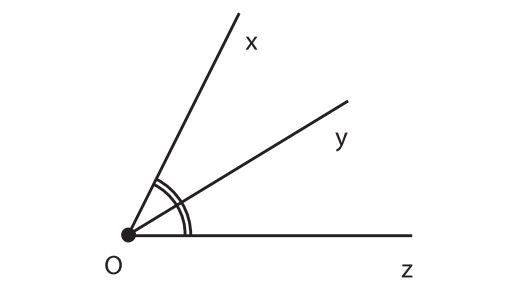 Tia phân giác của một góc
Tia phân giác của một góc
b. Tính chất của Tia Phân Giác
Tính chất chia đôi góc:
Tia phân giác của góc ∠ABC chia góc này thành hai góc bằng nhau:
∠ABD = ∠DBC. Trong đó BD là tia phân giác của góc ∠ABC.
Tính chất khoảng cách:
Bất kỳ điểm nào nằm trên tia phân giác của một góc đều cách đều hai cạnh của góc đó. Nếu điểm P nằm trên tia phân giác của góc ∠ABC thì khoảng cách từ P đến hai cạnh AB và BC là bằng nhau:
d(P, AB) = d(P, BC).
c. Cách Vẽ Tia Phân Giác
- Chia số đo góc thành hai phần bằng nhau.
- Vẽ tia phân giác nằm giữa hai cạnh của góc, sao cho góc tạo bởi một cạnh và tia phân giác bằng nửa số đo của góc đã cho.
2. Đường Phân Giác của Tam Giác
a. Khái niệm Đường Phân Giác
Đường phân giác của tam giác là đoạn thẳng kéo từ một đỉnh của tam giác đến cạnh đối diện, chia góc tại đỉnh đó thành hai góc bằng nhau. Mỗi tam giác đều có ba đường phân giác, và điểm giao nhau của ba đường phân giác này gọi là trọng tâm của tam giác.
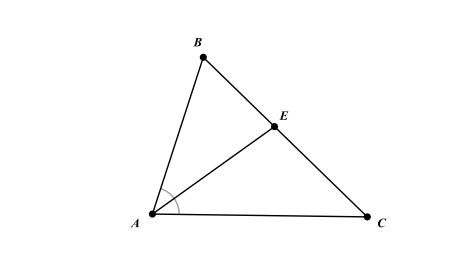 Đường phân giác của tam giác
Đường phân giác của tam giác
b. Tính Chất của Đường Phân Giác
Tính chất chia cạnh đối diện:
Đường phân giác của một góc trong tam giác chia cạnh đối diện thành hai đoạn tỷ lệ với hai cạnh kề của góc đó. Nếu đường phân giác của góc A trong tam giác ABC cắt cạnh BC tại điểm D, thì:
BD/DC = AB/AC.
Đường tròn nội tiếp:
Ba đường phân giác trong tam giác giao nhau tại một điểm duy nhất, gọi là tâm của đường tròn nội tiếp tam giác. Điểm này cách đều ba cạnh của tam giác và là tâm của đường tròn nội tiếp.
Độ dài đường phân giác:
Độ dài của đường phân giác trong tam giác có thể được tính bằng công thức:
[ d = frac{2bc}{b + c} cdot cosleft(frac{A}{2}right) ]
Trong đó a, b, c là độ dài các cạnh của tam giác, và A là góc đối diện với cạnh a.
Lưu ý: Công thức trên chỉ áp dụng cho trường hợp đường phân giác ngoài của tam giác.
II. Các Cách Chứng Minh Tia Phân Giác Lớp 9
1. Chứng Minh Bằng Định Nghĩa Tia Phân Giác
- Tia phân giác của một góc là tia nằm trong góc đó và chia góc này thành hai góc bằng nhau.
- Để chứng minh một tia là tia phân giác của góc, ta có thể sử dụng định nghĩa này.
Ví dụ, ta cần chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách Chứng Minh
- Xác định góc AOz và góc zOB.
- Chứng minh rằng ∠AOz = ∠zOB.
2. Chứng Minh Bằng Tam Giác Cân
- Nếu một điểm nằm trên tia phân giác của một góc thì điểm đó cách đều hai cạnh của góc.
Ví dụ, cần chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách Chứng Minh
- Xác định điểm P bất kỳ trên tia Oz.
- Chứng minh rằng khoảng cách từ P đến OA bằng khoảng cách từ P đến OB.
3. Chứng Minh Bằng Tính Chất Đường Tròn Nội Tiếp
- Nếu điểm nằm trên đường tròn nội tiếp tam giác và cách đều ba cạnh của tam giác, thì điểm đó là tâm của đường tròn nội tiếp.
Ví dụ, hãy chứng minh tia Oz là tia phân giác của góc ∠AOB:
+ Cách Chứng Minh
- Xác định tam giác AOB và đường tròn nội tiếp tam giác này.
- Chứng minh rằng Oz đi qua tâm của đường tròn nội tiếp và chia góc AOB thành hai góc bằng nhau.
4. Chứng Minh Bằng Các Tính Chất Của Tam Giác Đối Đẳng
- Nếu hai tam giác đối đẳng với nhau thì các cặp góc tương ứng bằng nhau.
Ví dụ, chứng minh tia Oz là tia phân giác của góc AOB:
+ Cách Chứng Minh
- Dùng các tam giác có chứa tia phân giác để chứng minh rằng các tam giác này đối đẳng, từ đó suy ra các góc tương ứng và tia phân giác.
Các cách chứng minh tia phân giác không chỉ giúp học sinh nắm vững kiến thức mà còn rèn luyện kỹ năng tư duy logic và khả năng áp dụng định lý, định nghĩa vào giải toán. Việc nắm rõ các phương pháp chứng minh tia phân giác sẽ là nền tảng vững chắc cho học sinh lớp 9 trong quá trình ôn thi và các kỳ thi quan trọng khác. Mong rằng bài viết này sẽ là tài liệu hữu ích cho các em trong quá trình học tập và ôn luyện.
Đừng quên tham khảo thêm các cuốn sách như Đại số và Hình học để nắm chắc cách giải tất cả các bài toán trong chương trình lớp 9 nhé!
Tìm hiểu thêm tại Tkbooks.vn!

 Nội Dung Sách Giới Tư Duy Toán Học
Nội Dung Sách Giới Tư Duy Toán Học Bố Mẹ Học Cùng Sách Giới Tư Duy Toán Học
Bố Mẹ Học Cùng Sách Giới Tư Duy Toán Học
 Tác giả Mai Phương chia sẻ bí quyết tăng từ 3 đến 4 điểm trong hai tháng ôn thi.
Tác giả Mai Phương chia sẻ bí quyết tăng từ 3 đến 4 điểm trong hai tháng ôn thi. Hướng dẫn giải chi tiết trong các cuốn sách luyện đề.
Hướng dẫn giải chi tiết trong các cuốn sách luyện đề. Chia sẻ của độc giả
Chia sẻ của độc giả
 Hình ảnh bài tập tự luận 1
Hình ảnh bài tập tự luận 1 Hình ảnh bài tập khó
Hình ảnh bài tập khó
 Ví dụ về dãy số tăng, dãy số giảm
Ví dụ về dãy số tăng, dãy số giảm Ví dụ về cấp số cộng
Ví dụ về cấp số cộng Bài tập ví dụ cơ bản về cấp số cộng
Bài tập ví dụ cơ bản về cấp số cộng Ví dụ về cấp số nhân
Ví dụ về cấp số nhân Bài tập về dãy số
Bài tập về dãy số Bài tập về cấp số cộng
Bài tập về cấp số cộng Bài tập về cấp số nhân
Bài tập về cấp số nhân
 Bài 5 – Phần trắc nghiệm – Phép trừ số có hai chữ số cho số có hai chữ số
Bài 5 – Phần trắc nghiệm – Phép trừ số có hai chữ số cho số có hai chữ số
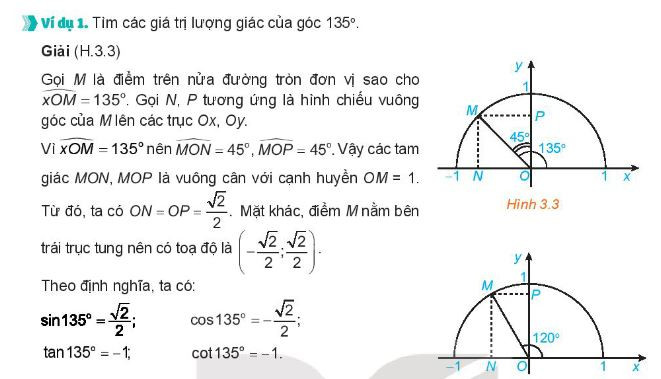 Giá Trị Lượng Giác
Giá Trị Lượng Giác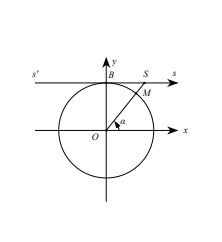 Ý Nghĩa Hình Học của Tang Cotang
Ý Nghĩa Hình Học của Tang Cotang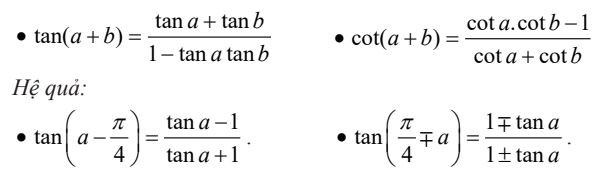 Công Thức Cộng Lượng Giác
Công Thức Cộng Lượng Giác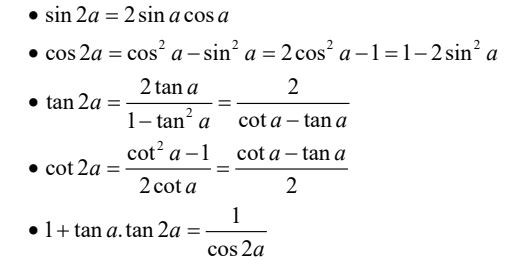 Công Thức Nhân Đôi Lượng Giác
Công Thức Nhân Đôi Lượng Giác Bài Tập Tìm Giá Trị Lượng Giác
Bài Tập Tìm Giá Trị Lượng Giác Cách Tính Giá Trị Lượng Giác Bằng Máy Tính
Cách Tính Giá Trị Lượng Giác Bằng Máy Tính
 Sách Chinh phục nâng cao Toán 3
Sách Chinh phục nâng cao Toán 3 Cuốn sách Để giỏi Toán con phải giỏi tính 3
Cuốn sách Để giỏi Toán con phải giỏi tính 3 Bộ sách Vở Bài tập nâng cao Toán 3
Bộ sách Vở Bài tập nâng cao Toán 3 Cuốn sách Phiếu bài tập cuối tuần Toán 3
Cuốn sách Phiếu bài tập cuối tuần Toán 3
