Danh mục: loigiaihay

Vectơ trong không gian và quan hệ vuông góc là một trong những kiến thức quan trọng trong chương trình Toán học phổ thông, đặc biệt là trong kỳ thi THPT Quốc gia. Kiến thức này chiếm khoảng 10% các bài toán và câu hỏi, do đó việc nắm vững lý thuyết và các dạng bài tập liên quan là cực kỳ quan trọng để đạt điểm số cao. Trong bài viết này, chúng ta sẽ đi sâu vào các khái niệm và ứng dụng của vectơ trong không gian và quan hệ vuông góc, nhằm giúp các bạn học sinh có sự chuẩn bị tốt nhất cho kỳ thi.

I. VECTƠ TRONG KHÔNG GIAN

1. Định nghĩa và các phép toán với vectơ trong không gian

Cho đoạn thẳng AB trong không gian. Nếu ta chọn điểm đầu là A và điểm cuối là B thì ta có một vectơ, ký hiệu là (vec{AB}).

Định nghĩa:
Vectơ trong không gian là một đoạn thẳng có hướng. Ký hiệu (vec{AB}) chỉ vectơ có điểm đầu là A và điểm cuối là B. Vectơ có thể được ký hiệu bằng (vec{a}, vec{b}, vec{x}, vec{y},)…

Các khái niệm liên quan đến vectơ như giá trị của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ không, sự bằng nhau của hai vectơ được định nghĩa tương tự như trong mặt phẳng.

>>> Click để xem thêm kiến thức về vectơ trong mặt phẳng

2. Điều kiện đồng phẳng của ba vectơ

a. Khái niệm về sự đồng phẳng của ba vectơ trong không gian

Trong không gian cho ba vectơ (vec{a}, vec{b}, vec{c}) đều khác vectơ không.

Nếu từ một điểm O bất kỳ ta vẽ (vec{OA} = vec{a}, vec{OB} = vec{b}, vec{OC} = vec{c}) thì có thể xảy ra hai trường hợp:

• Trường hợp các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng vectơ (vec{a}, vec{b}, vec{c}) không đồng phẳng.
• Trường hợp các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng thì ta nói ba vectơ (vec{a}, vec{b}, vec{c}) đồng phẳng. Trong trường hợp này giá trị của các vectơ (vec{a}, vec{b}, vec{c}) luôn song song với một mặt phẳng.

Chú ý: Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nêu trên không phụ thuộc vào việc chọn điểm O.

Từ đó ta có định nghĩa sau:

b. Định nghĩa

Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá trị của chúng cùng song song với một mặt phẳng.

II. HAI ĐƯỜNG THẲNG VUÔNG GÓC

1. Tích vô hướng của hai vectơ trong không gian

a. Góc giữa hai vectơ trong không gian

Định nghĩa:
Trong không gian, cho (vec{u}) và (vec{v}) là hai vectơ khác 0. Lấy một điểm A bất kỳ, gọi B và C là hai điểm sao cho (AB = vec{u}, AC = vec{v}).

Khi đó ta gọi góc BAC (0° < a < 180°).

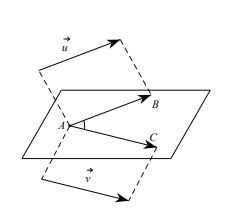Góc giữa hai vectơ trong không gian

b. Tích vô hướng của hai vectơ trong không gian

Định nghĩa:
Trong không gian, cho hai vectơ (vec{u}) và (vec{v}) là hai vectơ khác (vec{0}).

Tích vô hướng của hai vectơ (vec{u}) và (vec{v}) là một số, ký hiệu là (vec{u} cdot vec{v}) được xác định bởi công thức:

[
vec{u} cdot vec{v} = |vec{u}| cdot |vec{v}| cdot cos(vec{u}, vec{v})
]

Trong trường hợp (vec{u} = 0) hoặc (vec{v} = 0), ta quy ước (vec{u} cdot vec{v} = 0).

2. Vectơ chỉ phương của đường thẳng

a. Định nghĩa

Vectơ (vec{a}) khác 0 được gọi là vectơ chỉ phương của đường thẳng d nếu giá trị của vectơ (vec{a}) song song hoặc trùng với đường thẳng d.

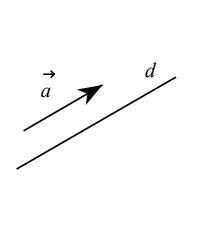Minh họa về vectơ chỉ phương của đường thẳng

b. Nhận xét

• Nếu (vec{a}) là vectơ chỉ phương của đường thẳng d thì vectơ (k cdot vec{a}) với (k neq 0) cũng là vectơ chỉ phương của d.
• Một đường thẳng trong không gian hoàn toàn xác định nếu biết một điểm A thuộc d và một vectơ chỉ phương (vec{a}) của nó.
• Hai đường thẳng song song với nhau khi và chỉ khi chúng là hai đường thẳng phân biệt và có hai vectơ chỉ phương cùng phương.

3. Góc giữa hai đường thẳng trong không gian

a. Định nghĩa

Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai vectơ chỉ phương của chúng.

Ví dụ minh họa góc giữa hai đường thẳng trong không gian

b. Nhận xét

Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

Nếu (vec{u}) là vectơ chỉ phương của đường thẳng a và (vec{v}) là vectơ chỉ phương của đường thẳng b thì ((vec{u}, vec{v}) = a) thì góc giữa hai đường thẳng a và b bằng a nếu 0° < a < 90°.

4. Hai đường thẳng vuông góc

a. Định nghĩa

Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.

Người ta ký hiệu hai đường thẳng a và b vuông góc với nhau là (a perp b).

b. Nhận xét

• Nếu (vec{u}) và (vec{v}) lần lượt là các vectơ chỉ phương của hai đường thẳng a và b thì (a perp b) nếu (vec{u} cdot vec{v} = 0).
• Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
• Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau.

5. Đường thẳng vuông góc với mặt phẳng

a. Định nghĩa

Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu d vuông góc với mọi đường thẳng nằm trong mặt phẳng (P).

Ví dụ minh họa về đường thẳng vuông góc với mặt phẳng

b. Điều kiện để đường thẳng vuông góc với mặt phẳng

Định lý:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

Hệ quả:
Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.

c. Tính chất

• Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
• Mặt phẳng trung trực của một đoạn thẳng AB vuông góc với AB là mặt phẳng trung trực của đoạn thẳng AB.

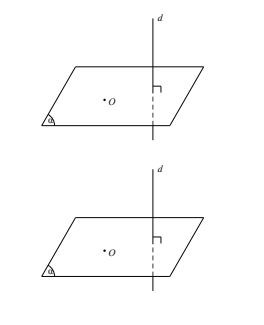Tính chất của đường thẳng vuông góc với mặt phẳng

6. Hai mặt phẳng vuông góc

6.1. Góc giữa hai mặt phẳng

Định nghĩa:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng thẳng đứng vuông góc với hai mặt phẳng.

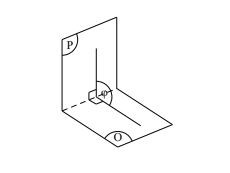Minh họa góc giữa hai mặt phẳng

6.2. Hai mặt phẳng vuông góc

Định nghĩa:
Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.

Kết luận

Trên đây là những kiến thức cơ bản về vectơ trong không gian và quan hệ vuông góc mà các bạn học sinh cần nắm vững. Việc làm quen và luyện tập với các dạng bài tập liên quan sẽ giúp các bạn chuẩn bị tốt cho kỳ thi THPT Quốc gia. Hãy thường xuyên ôn luyện và tham khảo thêm tài liệu tại loigiaihay.edu.vn để củng cố kiến thức của mình nhé!

Bài tập Tiếng Anh lớp 1 Unit 4 – In the Bedroom là tài liệu quan trọng giúp trẻ nắm vững từ vựng và cấu trúc câu liên quan đến chủ đề phòng ngủ. Với các bài tập được thiết kế sinh động, dễ hiểu, bé sẽ hứng thú hơn trong việc học tiếng Anh. Tài liệu đi kèm file PDF miễn phí rất tiện lợi cho phụ huynh và giáo viên trong việc hướng dẫn bé ôn luyện tại nhà.

Đặc biệt, tất cả các bài tập trong file đều bám sát theo chương trình học trong Unit 4 mà các bé lớp 1 đang theo học trên lớp!

Mời các bậc phụ huynh và giáo viên tham khảo cũng như tải về cho con ôn tập!

I. Bài tập Tiếng Anh lớp 1 Unit 4 – In the Bedroom

Dưới đây là các bài tập trong Unit 4 – In the Bedroom:

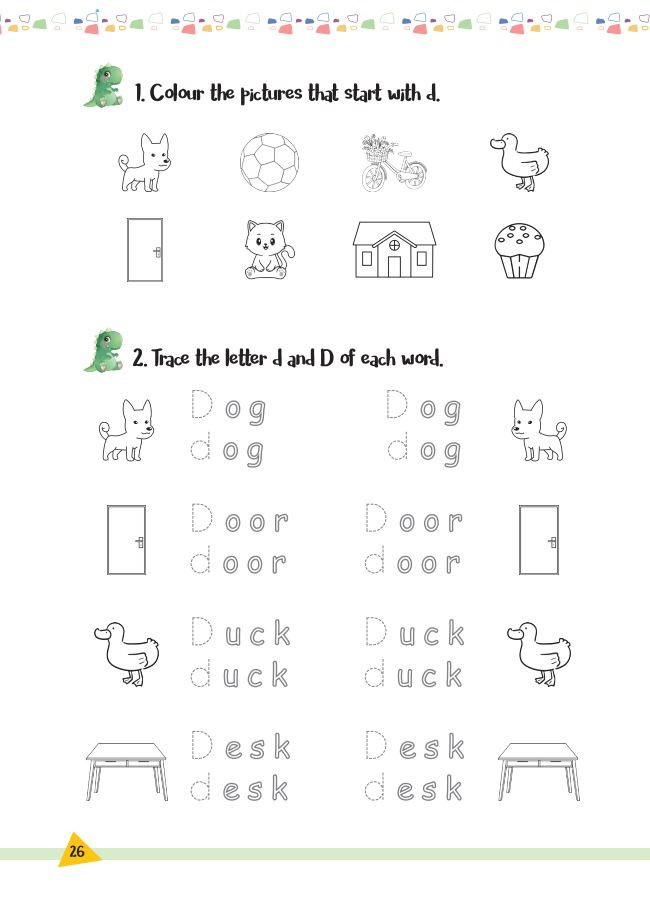
Bài tập Unit 4 – File 1

Bài tập Unit 4 – File 2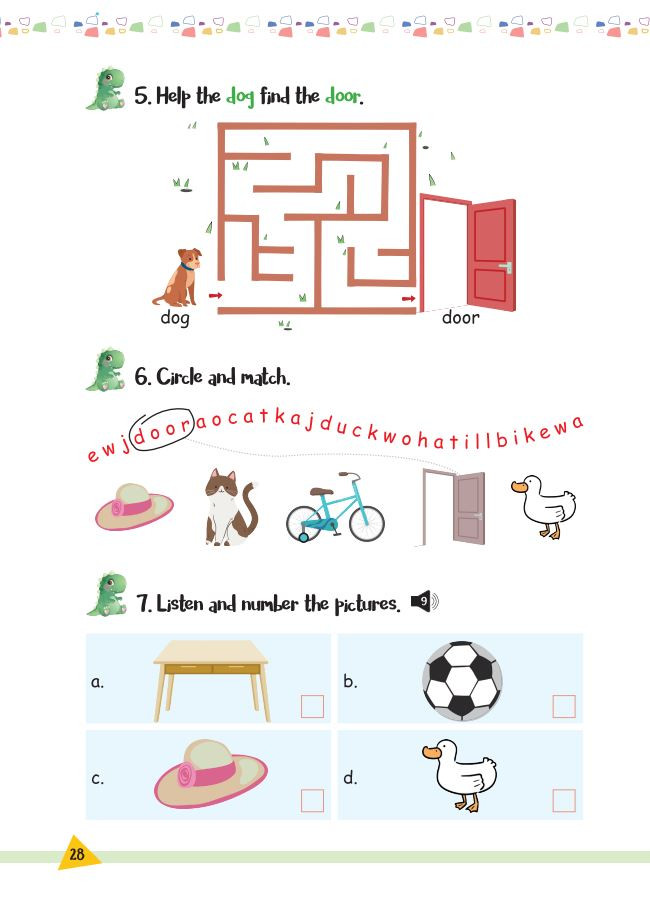

Bài tập Unit 4 – File 3

Bài tập Unit 4 – File 4

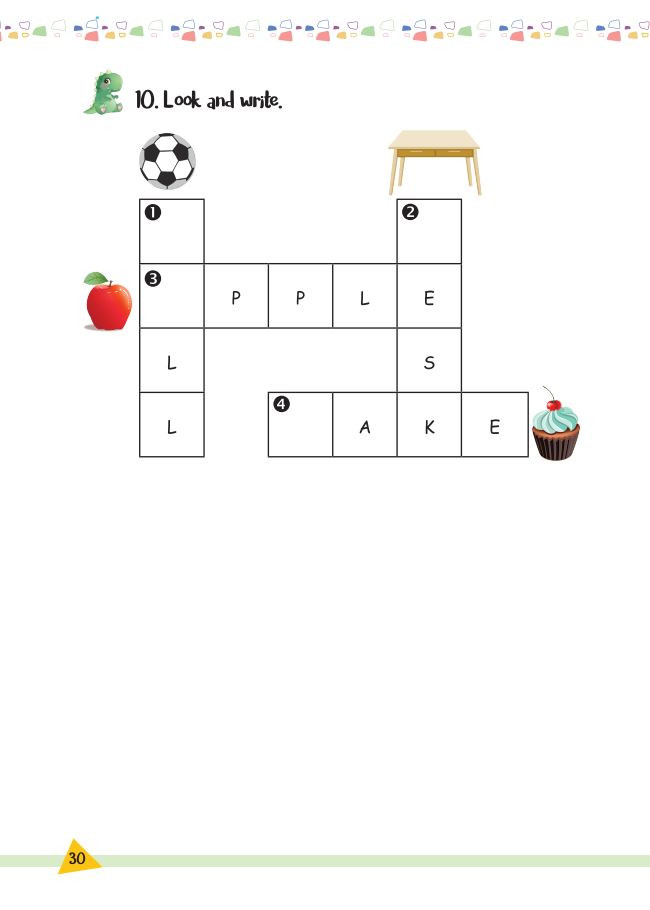Bài tập Unit 4 – File 5

Tải file bài tập PDF miễn phí tại đây!

II. Đáp án

Phụ huynh có thể kiểm tra đáp án cho các bài tập ở phần dưới đây nhé (đáp án cũng đã được đính kèm sẵn trong file PDF mà bố mẹ tải về cho con):

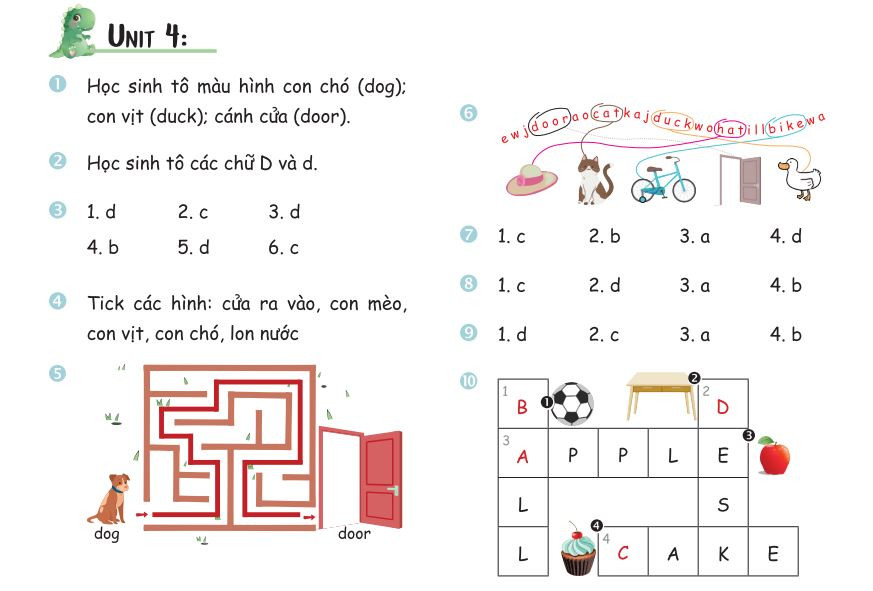Phần đáp án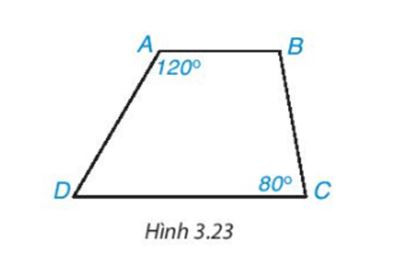

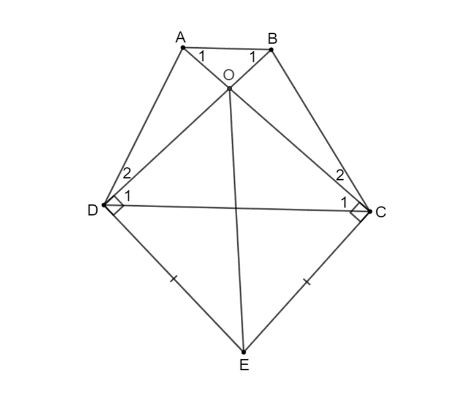Với Bài tập Tiếng Anh lớp 1 Unit 4 – In the Bedroom kèm file PDF, chắc chắn các bé sẽ tự tin hơn trong việc học tiếng Anh cũng như đạt điểm cao hơn trên lớp.

Những bài tập ở trên và bài tập của 15 Unit trong toàn bộ chương trình Tiếng Anh lớp 1 đều có sẵn trong cuốn Bài tập bổ trợ nâng cao Tiếng Anh lớp 1 của Tkbooks. Phụ huynh nên mua thêm sách để con có thể ôn và luyện tập thêm nhiều dạng bài tập khác.

Link đọc thử sách: https://drive.google.com/file/d/12oEmAYMnLrIQr89N05I3-AFh_3vmn7F5/view?usp=sharing

Hãy tải ngay file PDF để cùng con học tiếng Anh một cách hiệu quả và thú vị nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh lớp 1 hàng đầu tại Việt Nam!

Trong loạt bài viết này, chúng tôi sẽ cung cấp cho các học sinh lớp 8 một hướng dẫn chi tiết về các bài tập liên quan đến hình thang cân trong chương trình Toán học. Các bài tập này không chỉ giúp củng cố kiến thức mà còn cung cấp phương pháp giải bài mạch lạc, dễ hiểu.

Hãy cùng nhau giải quyết những bài tập ở phần Bài tập và Luyện tập chung (trang 55 – 56) nhé!

I. Phân Tích Bài Tập Hình Thang Cân

Bài 3.4. Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?

Hình vẽ bài 3.4

Lời giải:

• Cách 1:
  Hình thang ABCD có AB // CD nên ta có: Góc A + góc D = 180°.

  Do đó, góc D = 180° – góc A = 180° – 120° = 60°.

  Vì góc C khác góc D (góc C = 80° ≠ góc D = 60°), nên không phải là hình thang cân.

• Cách 2:
  Giả sử hình thang ABCD là hình thang cân. Khi đó góc A = góc B = 120°; góc C = góc D = 80°.

  Suy ra góc A + góc B + góc C + góc D = 120° + 120° + 80° + 80° = 400° > 360° (không thoả mãn định lí tổng bốn góc trong một tứ giác).

  Do đó, ABCD không phải là một tứ giác, điều này mâu thuẫn với giả thiết ABCD là hình thang cân.

  Vậy ABCD không phải là hình thang cân.

Bài 3.5 (trang 55 Toán 8 Tập 1): Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

Gọi O là giao điểm của AC và BD.

Hình vẽ bài 3.5

Xét tam giác DOE và tam giác COE có:

Góc ODE = góc OCE = 90° (Vì OD ⊥ DE; OC ⊥ CE); EC = ED (giả thiết);

Cạnh OE chung.

Vì vậy tam giác DOE = tam giác COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng) (1).

Từ đó tam giác OCD cân tại O nên góc C1 = góc D1.

Vì ABCD là hình thang nên AB // CD suy ra góc A1 = góc C1; góc B1 = góc D1 (cặp góc so le trong).

Do đó góc A1 = góc B1 (vì góc C1 = góc D1).

Suy ra tam giác OAB cân tại O nên OA = OB (2).

Ta có: AC = DA + OC và BD = OB + OD (3).

Từ (1), (2) và (3) suy ra AC = BD.

Hình thang ABCD có AC = BD nên ABCD là hình thang cân.

Bài 3.6 (trang 55 Toán 8 Tập 1): Vẽ hình thang cân ABCD (AB // CD) biết đáy dài CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.

Lời giải:

Cách vẽ hình thang cân ABCD:

• Vẽ cạnh CD = 4 cm.
• Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.
• Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.
• Nối AB, AD, BC ta được hình thang cân ABCD như hình vẽ.

Hình vẽ bài 3.6

Bài 3.7 (trang 55 Toán 8 Tập 1): Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Lời giải:

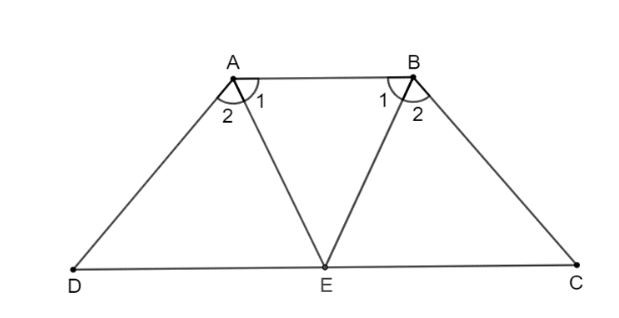Hình vẽ bài 3.7

Vì ABCD là hình thang cân nên góc DAB = góc ABC; góc C = góc D; AD = BC.

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của góc BAD và góc ABC.

Suy ra góc A1 = góc A2 = ½ góc DAB; góc B1 = góc B2 = ½ góc ABC. Mà góc DAB = góc ABC nên góc A1 = góc A2 = góc B1 = góc B2.

Xét tam giác EAB cân tại E (vì góc A1 = góc B1) nên EA = EB.

Xét tam giác ADE và tam giác BCE có:

EA = EB (chứng minh trên);

Góc A2 = góc B2 (chứng minh trên);

AD = BC (chứng minh trên).

Do đó tam giác ADE = tam giác BCE (c.g.c).

Suy ra EC = ED (hai cạnh tương ứng).

Bài 3.8 (trang 55 Toán 8 Tập 1): Hình thang cân ABCD (AB // CD) có AB = CD.

Lời giải:

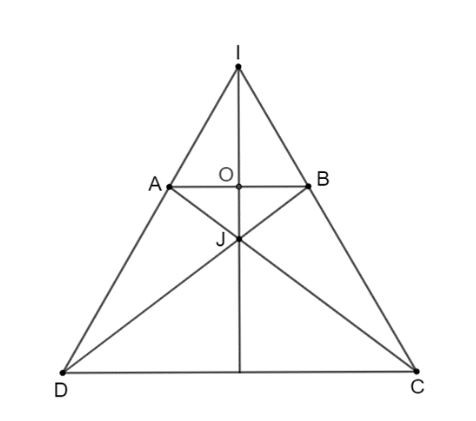Hình vẽ bài 3.8

Vì ABCD là hình thang cân nên góc BAD = góc ABC; góc ADC = góc BCD; AD = BC; AC = BD.

Xét DICD cân tại I (vì góc ADC = góc BCD) nên IC = ID.

Suy ra IC – BC = ID – AD, hay IB = IA.

Do đó I cách đều A và B nên I nằm trên đường trung trực của AB (1).

Xét tam giác ABD và tam giác BAC có:

AB là cạnh chung,

Góc BAD = góc ABC (chứng minh trên);

AD = BC (chứng minh trên).

Do đó tam giác ABD = tam giác BAC (c.g.c).

Suy ra góc ABD = góc BAC (hai góc tương ứng).

Tam giác JAB cân tại J (vì góc ABD = góc BAC) nên JA = JB.

Do đó J cách đều A và B nên J nằm trên đường trung trực của AB (2).

Từ (1) và (2) suy ra I, J cùng nằm trên đường thẳng IJ là đường trung trực của đoạn thẳng AB.

II. Phần Luyện Tập Chung Về Hình Thang Cân

Bài 3.9 (trang 56 Toán 8 Tập 1): Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

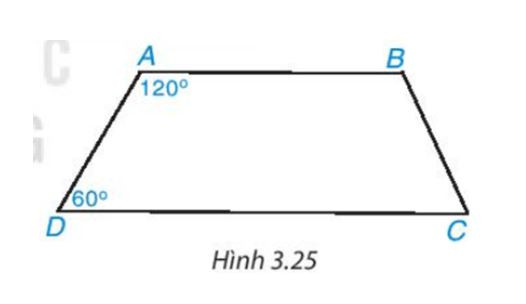Hình vẽ bài 3.9

Lời giải:

Vẽ tia Dx đi qua điểm A.

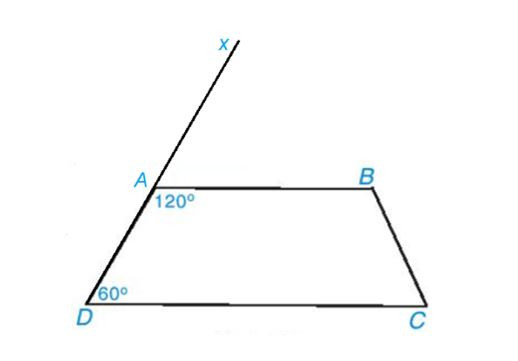Hình vẽ cho lời giải bài 3.9

Vì góc DAB và góc BAx là hai góc kề bù nên góc DAB + góc BAx = 180°.

Suy ra góc BAx = 180° – góc DAB = 180° – 120° = 60°.

Ta có góc ADC = góc BAx = 60° mà hai góc này ở vị trí đối diện nên AB // CD.

Vậy tứ giác ABCD là hình thang.

Bài 3.10 (trang 56 Toán 8 Tập 1): Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết ABD = 30°, tính số đo các góc của hình thang đó.

Lời giải:

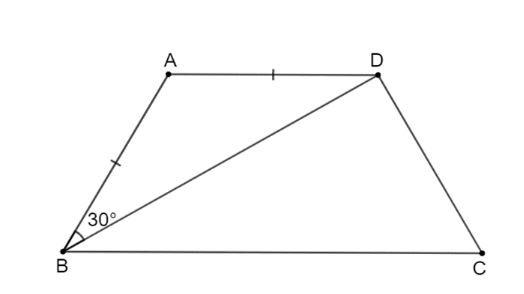Hình vẽ bài 3.10

Xét tam giác ABD cân tại A (vì AB = AD), ta có:

Góc ADB = góc ABD = 30°;

Góc A + góc ABD + góc ADB = 180° hay góc A + 30° + 30° = 180°.

Suy ra góc A = 180° – 30° – 30° = 120°.

Vì AB // CD nên góc ADB = góc CBD = 30° (hai góc so le trong).

Do đó góc ABC = góc ABD + góc CBD = 30° + 30° = 60°.

Vì tứ giác ABCD là hình thang cân nên góc C = góc ABC = 60°; góc ADC = góc A = 120°.

Vậy số đo các góc của hình thang cân ABCD là: góc A = 120°; góc ABC = 60°; góc C = 60°; góc ADC = 120°.

Bài 3.11 (trang 56 Toán 8 Tập 1): Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

Hình vẽ bài 3.11

Lời giải:

Xét tam giác ABD cân tại A (vì AB = AD) ta có:

Góc ADB = góc ABD = 40°.

Góc A + góc ABD + góc ADB = 180°.

Suy ra góc A = 180° – góc ABD – góc ADB = 180° – 40° – 40° = 100°.

Ta có góc ADB + góc BDC = 120° suy ra góc BDC = 120°.

Xét tam giác BCD cân tại C (vì BC = CD) ta có:

Góc CBD = góc CDB = 80°.

Góc C + góc CBD + góc CDB = 180°.

Suy ra góc C = 180° – góc CBD – góc CDB = 180° – 80° – 80° = 20°.

Ta có: Góc ABC = góc ABD + góc CBD = 40° + 80° = 120°.

Vậy số đo các góc của tứ giác ABCD là: Góc A = 100°; góc ABC = 120°; góc C = 20°.

Bài 3.12 (trang 56 Toán 8 Tập 1): Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân.

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Lời giải:

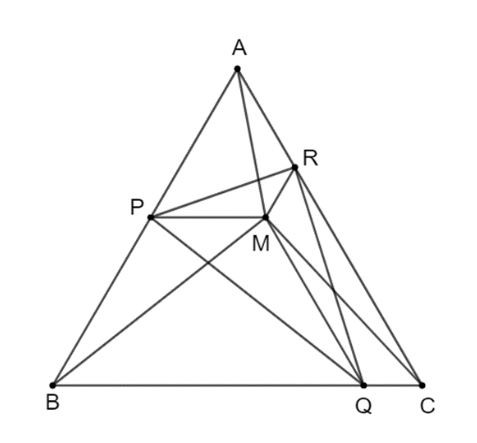Hình vẽ bài 3.12

a) Vì tam giác ABC đều nên góc BAC = góc ABC = góc ACB = 60°.

Vì PM // BC nên APM = ABC = 60° (đồng vị).

Suy ra góc APM = góc PAR (cùng bằng 60°).

Tứ giác APMR là hình thang (vì MR // AP) có góc APM = góc PAR.

b) Vì tứ giác APMR là hình thang cân nên AM = PR (1).

Chứng minh tương tự câu a, ta cũng có các tứ giác BPMQ và MQCR là hình thang cân.

Suy ra BM = PQ và MC = QR (2).

Từ (1) và (2) suy ra PR + PQ + QR = MA + MB + MC.

Mà PR + PQ + QR chính là chu vi của tam giác PQR.

Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).

c) Để tam giác PQR là tam giác đều thì PR = PQ = QR. Suy ra MA = MB = MC.

Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.

Vì vậy, M là giao điểm của ba đường trung trực (đường thẳng đi qua trung điểm của các cạnh và vuông góc với các cạnh đó).

Hi vọng rằng phần giải bài tập Toán lớp 8 tập 1 bài 11 trang 51: Hình thang cân ở trên của chúng tôi sẽ giúp các em hiểu rõ hơn về cách áp dụng kiến thức vào giải các bài toán về hình thang cân, đồng thời cũng củng cố thêm sự tự tin trong quá trình học tập môn Toán.

Hãy tiếp tục ôn luyện và thực hành thường xuyên để nắm vững các kiến thức cơ bản, từ đó chuẩn bị tốt nhất cho các kỳ thi sắp tới.

Chúc các em học tập hiệu quả và đạt được kết quả cao!

Các dạng toán và lý thuyết ở trên đều có sẵn trong cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 8 – Tập 1. Các em nên mua cuốn sách này để hỗ trợ cho việc học Toán của mình nhé! Ngoài ra TKbooks cũng có đủ bộ sách tham khảo lớp 8 của môn Ngữ Văn và Tiếng Anh với nội dung bám sát chương trình học mới nhất.

Link để thử sách: https://drive.google.com/file/d/1TsmoDs83uAwQu0FqU6ikrzFtEBDMH2Kq/view

TKbooks tự hào là nhà xuất bản sách tham khảo lớp 8 hàng đầu tại Việt Nam!

TKbooks.vn

Bài tập số chẵn số lẻ lớp 4 dưới đây cung cấp cho các em hệ thống bài tập từ cơ bản đến nâng cao, bao gồm cả trắc nghiệm và tự luận, bám sát chương trình Kết nối tri thức với cuộc sống. Qua việc thực hành và luyện tập với các bài tập này, các em sẽ hiểu rõ dấu hiệu nhận biết, quy luật và cách tính toán với số chẵn, số lẻ, từ đó làm các bài tập tương tự nhanh và chính xác hơn.

Mời quý phụ huynh và các em tham khảo!

>>> Xem thêm:

Bảng đơn vị đo diện tích lớp 4 kèm bài tập và lời giải chi tiết

5 Đề thi Toán lớp 4 học kỳ 1 Kết nối tri thức PDF

I. Bài tập trắc nghiệm

Bài 1: Số lớn nhất có 5 chữ số là?

Số lẻ lớn nhất có 4 chữ số là	9999
Số chẵn lớn nhất có 4 chữ số là	9998
Số lẻ lớn nhất có 4 chữ số khác nhau là	9876
Số lớn nhất có 4 chữ số khác nhau là	9875

Bài 2: Dấu hiệu nhận biết một số là số chẵn là:

A. Số đó chia hết cho 2
B. Số có tận cùng là 0; 2; 4; 6; 8
C. Cả A và B đều sai
D. Cả A và B đều đúng

Bài 3: Dấu hiệu nhận biết một số là số lẻ là:

A. Số đó không chia hết cho 2
B. Số có tận cùng là 1; 3; 5; 7; 9
C. Cả A và B đều sai
D. Cả A và B đều đúng

Bài 4: Số chẵn nhỏ nhất có năm chữ số khác nhau:

A. 12 340
B. 10 342
C. 10 234
D. 10 432

Bài 5: Số liền trước của số chẵn nhỏ nhất có năm chữ số khác nhau là:

A. 10 324
B. 10 432
C. 10 234
D. 10 233

>>> Tải file bài tập dưới dạng PDF miễn phí tại đây!

Bài 6: Hai số chẵn liên tiếp hơn kém nhau bao nhiêu đơn vị?

A. 3
B. 1
C. 2
D. 0

Bài 7: Hai số lẻ liên tiếp hơn kém nhau bao nhiêu đơn vị?

A. 2
B. 3
C. 1
D. 0

Bài 8:

Tổng của hai số là 237. Biết số bé là số chẵn bé nhất có ba chữ số. Tìm số lớn.
A. 137
B. 135
C. 98
D. 200

Bài 9: Số chẵn là số?

A. Chia hết cho số 3
B. Có tận cùng là số 5
C. Chia hết cho số 2
D. Không chia hết cho 3

Bài 10: Số chẵn lớn nhất có sáu chữ số được là:

A. Chín trăm chín mươi chín triệu chín trăm chín mươi chín
B. Chín trăm chín mươi chín triệu chín trăm chín mươi tám
C. Chín trăm chín mươi chín triệu không chín trăm chín mươi tám
D. Chín trăm chín mươi chín triệu một trăm chín mươi chín không tám

Bài 11:

Tìm số tự nhiên x biết x là số chẵn lớn nhất sao cho 151
A. 158
B. 156
C. 168
D. 166

Bài 12:

Trong dãy số tự nhiên, hai số chẵn liên tiếp hơn kém nhau mấy đơn vị?
A. 1 đơn vị
B. 0 đơn vị
C. 3 đơn vị
D. 2 đơn vị

Bài 13: Từ 0 đến 20 có bao nhiêu số lẻ?

A. 9 số
B. 10 số
C. 11 số
D. 20 số

Bài 14:

Cho dãy số: 205; 207; 209; …; 217; 219; 221. Các số thích hợp điền vào chỗ chấm lần lượt là:
A. 201; 203; 215
B. 212; 214; 216
C. 210; 212; 214
D. 211; 213; 215

Bài 15: Các số lẻ thích hợp điền vào dấu chấm là?

13, 15, 17, …, 21, …, …, 27
A. 18, 19, 21
B. 19, 23, 25
C. 19, 20, 22
D. 21, 23, 25

Bài 16: Từ 10 đến 39 có bao nhiêu số chẵn?

A. 15
B. 30
C. 14
D. 29

Bài 17: Nối phép tính có cùng kết quả:

2400 × 2	1230 – (300 – 150)	783:3
Số lẻ	Số chẵn
—	—

Bài 18:

Từ các số 1, 4, 5, 2 có thể lập được bao nhiêu số chẵn có hai chữ số khác nhau?
A. 3
B. 5
C. 4
D. 6

II. Bài tập tự luận

Bài 1:

Biết tổng của ba số chẵn liên tiếp bằng 444. Tìm ba số đó.
Bài làm
………………………………………….

Bài 2: Hãy lấy 5 ví dụ:

a. Là số chẵn: …………………………………………..
b. Là số lẻ: ……………………………………………
c. Là số có 4 chữ số và chia hết cho 2: …………………………………………………..
d. Là số có 5 chữ số và không chia hết cho 2: ……………………………………………….

Bài 3:

Có tất cả bao nhiêu số lẻ có 3 chữ số?
Bài làm
……………………………………….

Bài 4:

Trong các số dưới đây, số nào là số chẵn, số nào là số lẻ?
189; 62123; 6514; 24252; 41427; 2185; 32928; 756
Số chẵn là: …………………………………………..
Số lẻ là: …………………………………………..

Bài 5: Điền vào chỗ trống:

314; 316; …; …; …; 324
295; 297; …; …; …; 305

Bài 6: Viết số thích hợp vào chỗ trống để được:

a. Ba số chẵn liên tiếp:
782; …; …
…; …; 550
…; 920; …

b. Ba số lẻ liên tiếp:
7561; …; …
…; …; 8001
…; 7687; …

Bài 7: Cho các thể số: 8; 0; 7; 5

a. Lập các số chẵn có 4 chữ số
…; …; …; …; …; …; …
b. Lập các số lẻ có 4 chữ số
…; …; …; …; …; …; …

Bài 8:

Không cần làm tính, kiểm tra kết quả của phép tính sau đây đúng hay sai?
a. 1783 + 9789 + 375 + 8001 + 2797 = 22744
Bài làm
………………………………………………

b. 1872 + 786 + 3748 + 3718 = 10115
Bài làm
………………………………………………

c. 5674 x 163 = 610783
Bài làm
………………………………………………

Bài 9:

Bạn Toán tính tổng các chẵn trong phạm vi từ 20 đến 98 được 2025. Không thực hiện tính tổng em cho biết Toán tính đúng hay sai?
Bài làm
………………………………………………

Bài 10:

Tổng tính tổng của các số lẻ từ 21 đến 99 được 2025. Không tính tổng em cho biết Tổng tính đúng hay sai?
Bài làm
………………………………………………

Bài 11:

Tiến làm phép chia 1935 : 9 được thương là 216 và không còn dư. Không thực hiện cho biết Tiến làm đúng hay sai?
Bài làm
………………………………………………

Bài 12:

Cho 2021 số tự nhiên, trong đó tổng 5 số tự nhiên bất kỳ là số lẻ. Hỏi tổng 2021 số tự nhiên là lẻ hay chẵn?
Bài làm
………………………………………………

Bài 13:

Dùng cả bốn số sau ghép thành các số lẻ có 3 chữ số khác nhau: 2; 7; 6; 3.
Bài làm
………………………………………………

Bài 14: Tính tổng các số lẻ từ 21 đến 38.

Bài làm
………………………………………………

Bài 15:

Hàng cây ven đường được đánh số như sau:
Cây thứ nhất đánh số 1; Cây thứ 2 đánh số 3;
Cây thứ 3 đánh số 5; …
Hỏi cây thứ 200 đánh số mấy?
Hình ảnh minh họa

Hy vọng bộ bài tập số chẵn số lẻ lớp 4 – Kết nối tri thức PDF ở trên đã giúp các em củng cố kiến thức, rèn luyện kỹ năng nhận biết và tính toán với số chẵn, số lẻ một cách thành thạo.

Các bài tập trên đều có sẵn trong cuốn Bài tập bổ trợ nâng cao Toán lớp 4 và 50 đề tăng điểm nhanh Tiếng Anh lớp 4. Các em hãy mua ngay hai cuốn sách này để học tốt môn Toán hơn nhé!

Link đọc thử sách Bài tập bổ trợ nâng cao Toán lớp 4: https://drive.google.com/file/d/196iDHopU1z89arXXqkQBU4QkSII1X92m/view

Link đọc thử sách 50 đề tăng điểm nhanh Toán lớp 4: https://drive.google.com/file/d/1GxTFdbwB-LbWNLrpRrlbMj2EMr1U9-X4/view

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 4 hàng đầu tại Việt Nam!

Tkbooks.vn

Các em đang tìm kiếm cách viết đoạn văn thể hiện tình cảm, cảm xúc qua một câu chuyện hay và ý nghĩa? Bài viết dưới đây sẽ giúp các em!

Trong bài viết này, chúng tôi sẽ cung cấp cho các em dàn ý và các bài văn mẫu chuẩn để các em tham khảo. Hãy cùng khám phá ngay để nâng cao kỹ năng viết văn của mình nhé!

I. Dàn Ý Cho Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Một Câu Chuyện

1. Mở Bài

• Giới thiệu chung về câu chuyện và cảm xúc ban đầu.
• Nhắc đến câu chuyện (tên câu chuyện), tôi luôn cảm thấy… (ấn tượng, xúc động, khám phá, tiếc nuối…).
• Câu chuyện không chỉ hấp dẫn mà còn mang đến nhiều bài học ý nghĩa.

2. Thân Bài

Trình bày tình cảm, cảm xúc của các nhân vật và tình tiết trong câu chuyện.

Nhân vật chính/nên bạn ấn tượng:

• Cảm thấy yêu mến, khám phá hay thương cảm? Vì sao?
• Hành động, tính cách nào của nhân vật gây ấn tượng sâu sắc?
• Tình tiết nào khiến mình xúc động hoặc ấn tượng nhất?
• Tình tiết nào khiến mình vui, buồn, hồi hộp hay suy ngẫm?
• Những chi tiết đó mang ý nghĩa gì, gợi lên điều gì trong lòng mình?

Bài học rút ra từ câu chuyện:

• Câu chuyện giúp mình hiểu thêm điều gì về cuộc sống, về đạo đức, về tính người?
• So sánh với thực tế, câu chuyện mang ý nghĩa gì đối với bản thân và mọi người?

3. Kết Bài

• Khẳng định lại cảm xúc và ý nghĩa câu chuyện.
• Câu chuyện không chỉ mang đến bài học sâu sắc mà còn để lại dấu ấn khó quên trong lòng tôi.
• Qua đó, tôi càng thêm yêu thích những câu chuyện giàu ý nghĩa của văn học dân gian/văn học hiện đại.

II. Bài Văn Mẫu

1. Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Câu Chuyện “Sơn Tinh, Thủy Tinh”

Mỗi lần nhắc lại câu chuyện “Sơn Tinh, Thủy Tinh”, tôi không khỏi khâm phục tài trí và sức mạnh của Sơn Tinh, đồng thời lại thấy thương cảm và tiếc nuối cho Thủy Tinh. Sơn Tinh quả thực là một vị thần tài giỏi, có thể dời núi, nâng đất, mang đến sự phồn vinh cho con người. Nhưng Thủy Tinh cũng không hề kém cạnh, chỉ vì tình yêu không thành mà lòng cảm giác hóa thành cơn giận dữ. Năm nào cũng vậy, lúc nửa đêm lại nhắc nhở về cuộc chiến xưa, khiến tôi cảm nhận rõ hơn về sức mạnh thiên nhiên và ý chí kiên cường của con người trong cuộc đấu tranh bảo vệ cuộc sống. Câu chuyện không chỉ hấp dẫn mà còn mang đến bài học quý giá: thiên nhiên có thể hung dữ, nhưng nếu con người đoàn kết, kiên trì, chúng ta sẽ luôn chiến thắng.

Hình minh họa cho câu chuyện

2. Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Câu Chuyện “Sự Tích Sầu Đâu”

Câu chuyện “Sự Tích Sầu Đâu” luôn khiến tôi xúc động và khám phá điều kỳ diệu của những con người khuyết tật. Sinh ra với ngoại hình khác biệt, Sầu Đâu từng bị mọi người coi thường, nhưng cậu không bao giờ buồn bã hay tự ti mà luôn chăm chỉ, hiểu thảo với mẹ. Tôi cảm thấy vui mừng khi nhớ tới tài năng và sự tốt bụng của Sầu Đâu, cậu đã tìm được hạnh phúc bên người vợ hiền, chung thủy. Điều đặc biệt, chi tiết Sầu Đâu lấp láy sắp xếp để trở thành chàng trai khôi ngô khiến tôi nhận ra rằng chúng ta không thể đánh giá con người qua vẻ bề ngoài. Câu chuyện dạy tôi bài học về lòng nhân ái và niềm tin vào những điều tốt đẹp trong cuộc sống.

Hình minh họa cho câu chuyện

3. Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Câu Chuyện “Thạch Sanh”

Câu chuyện “Thạch Sanh” khiến tôi vô cùng ngưỡng mộ và khám phá lòng dũng cảm, chính trực của nhân vật chính. Từ một chàng trai mồ côi, sống nghèo khổ, Thạch Sanh vẫn không oán trách số phận mà luôn kiên cường, trung thực. Tôi thích nhất chi tiết Thạch Sanh một mình chiến đấu với Chằn Tinh và Đại Bàng để cứu người, thể hiện phẩm chất anh hùng đáng quý. Khi bị kẻ gian hãm hại, Thạch Sanh vẫn kiên nhẫn chờ đợi cơ hội, điều này làm tôi cảm thấy yêu mến và tôn trọng hơn sự ngay thẳng, chân thành trong cuộc sống. Câu chuyện mang đến bài học rằng những người hiền lành, dũng cảm sẽ luôn giành được thắng lợi, còn kẻ gian ác cuối cùng cũng sẽ phải chịu thất bại.

Hình minh họa cho câu chuyện

4. Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Câu Chuyện “Cây Tre Trăm Đốt”

Câu chuyện “Cây Tre Trăm Đốt” vừa khiến tôi thích thú, vừa làm tôi cảm thấy căm ghét sự tham lam, gian dối của nhân vật lão phú ông. Anh nông dân hiền lành, chăm chỉ, với lòng yêu thương con gái phú ông nhưng lại bị lừa dối và chịu nhiều thiệt thòi. Tôi vô cùng hài hước khi cuối cùng anh đã lấy lại công bằng bằng sự giúp đỡ của Bụt. Hình ảnh cây tre trăm đốt như một phép màu nhiệm, vật chất tốt đẹp mang lại hạnh phúc cho người tốt. Qua câu chuyện, tôi nhận ra rằng cuộc sống luôn có nhân quả, những ai sống chân thành, thật thà rồi sẽ nhận được điều tốt đẹp.

Hình minh họa cho câu chuyện

5. Đoạn Văn Thể Hiện Tình Cảm, Cảm Xúc Qua Câu Chuyện “Sự Tích Hồ Gươm”

Câu chuyện “Sự Tích Hồ Gươm” làm tôi cảm thấy tự hào và xúc động về tinh thần yêu nước của dân tộc ta. Hình ảnh Lê Lợi nhận được thanh gươm thần để đánh đuổi giặc ngoại xâm hiện niềm tin rằng chính nghĩa luôn chiến thắng.

Hình minh họa cho câu chuyện

Hy vọng bài viết trên đã giúp các em hiểu rõ hơn cách viết đoạn văn thể hiện tình cảm, cảm xúc qua một câu chuyện. Hãy áp dụng dàn ý và bài mẫu để tự viết những đoạn văn hay cho riêng mình nhé!

Các bài tập đọc này không chỉ giúp bé phát triển kỹ năng đọc hiểu mà còn tăng cường vốn từ và phát triển ngôn ngữ, từ đó chuẩn bị cho bé những kiến thức cần thiết để hoàn thành tốt các bài kiểm tra trong lớp và đạt điểm cao hơn môn Tiếng Việt.

Mời quý phụ huynh và các em tham khảo!

Bài Tập Đọc Số 1

Chú Chuột Chuyện Nước

Ôi chao! Chú chuột chuyện nước mới đẹp làm sao! Màu vàng trên lưng chú lấp lánh. Bốn cái cánh mỏng như giấy bóng. Cái đầu tròn và hai con mắt long lanh như hạt tiểu tinh.

Thân hình chú nhảy và thon, và vàng như màu vàng của nắng mùa thu. Chú đậu trên một cành lá lục vươn dài trên mặt hồ. Bốn cánh khẽ rung rung như đang còn phân vân.

(Nguyễn Thế Hợi)

Bài Tập Đọc Số 1 – Chú Chuột Chuyện Nước

Bài Tập Đọc Số 2

Đeo Chuông Cho Mèo

Trong một cửa hàng bách hóa nhỏ có rất nhiều chuột. Hàng ngày, chúng phá phách và làm hư hỏng rất nhiều hàng hóa. Vì vậy, chủ tiệm đã quyết định mua một con mèo để dẹp yên lũ chuột này. Đến chuột rất lo lắng vì điều đó và tìm cách tự cứu lấy mình.

Bây giờ một con chuột nhất mới lên tiếng: “Tôi xin có ý kiến. Nếu chúng ta bị bắt là bởi vì chúng ta không biết khi nào mèo đến gần chúng ta. Bây giờ, chúng ta hãy đeo cái chuông này quanh cổ mèo. Như vậy, khi nào mèo đến gần, chúng ta sẽ đều nghe rõ và dễ dàng lẩn trốn.” Lời đề nghị này được mọi người khen hay.

Cho đến một lúc sau, một con chuột già đứng dậy và nó nói:

“Tốt lắm, thế nhưng ai sẽ là người đeo chuông cho mèo đây?”

Lũ chuột cũ kia nhìn con kia không con nào nói gì. Thấy vậy, chuột già bảo:

“Nói thì bao giờ cũng dễ nhưng làm thì mới khó.”

(Truyền ngụ ngôn)

Bài Tập Đọc Số 2 – Đeo Chuông Cho Mèo

Bài Tập Đọc Số 3

Xiếc Thú

Ai xem xiếc, bé thích nhất là tiết mục xiếc thú.

Thoát đầu, cả đàn khỉ chạy ùa ra. Các chú kiểng chân, chưa kịp nghiêng mình chào khán giả đã bắt đầu đua xe đạp. Các chú ngã hấp tấp, khiến luôn cả xe đạp mất lái.

Sau đó là tiết mục xiếc chó lớn. Chú siêng năng, cô giáo khen cho quà. Chú biểu nhạc, chẳng làm việc gì, bị cô giáo chê. Có chú nghiêng đầu, tưởng vẻ đang tính toán. Có chú còn liếc sang bên cạnh. Cũng có chú mất trọng tài khắp lớp.

(Nguồn: Internet)

Bài Tập Đọc Số 3 – Xiếc Thú

Bài Tập Đọc Số 4

Lời Khuyên Của Bố

Học quả là khó khăn, gian khổ. Bố muốn con đến trường với niềm hăng say và niềm phấn khởi. Con hãy nghĩ đến những người thật, tôi đến trường sau một ngày lao động vất vả. Cả những

người lính vừa ở thao trường vừa lăn ngay vào bần đọc đọc, viết viết. Con hãy nghĩ đến các em nhỏ bị cấm đi học mà vẫn thích học.

Con hãy tưởng tượng mà xem, nếu phong trào học tập ấy bị ngưng lại thì nhân loại sẽ chìm đắm trong cảnh ngu dốt, trong sự dã man. Bố tin rằng con sẽ luôn cố gắng và không bao giờ là người lính hèn nhát trên mặt trận đầy gian khổ ấy.

(Theo A-mi-xi)

Bài Tập Đọc Số 5

Cô Giáo Lớp Em

Sáng nào em đến lớp

Cũng thấy cô đến rồi

Dập lại “Chào cô ạ!”

Cô mỉm cười thật tươi.

Cô dạy em tập viết

Gió đưa thoảng hương nài

Nắng ghé vào cửa lớp

Xem chúng em học bài.

Những lời cô giáo dạy

âm trang vỗ thầm tho

Yêu thương em ngắm mãi

Những điều mượn cô cho.

(Nguyễn Xuân Sanh)

Bài Tập Đọc Số 6

Bàn Tay Cô Giáo

Bàn tay cô giáo

Tết tóc cho em

Và nhắc mẹ khen

Tay cô rất khéo

Bàn tay cô giáo

Cô cầm tay em

Và áo cho em

Như tay chị cả

Như tay mẹ hiền

Nắn từng nét chữ

Em viết đẹp thêm

Để điểm mười trang vở

(Đình Hải)

Bài Tập Đọc Số 7

Lòng Mẹ

Có miếng ngọt, miếng ngon

Mẹ dành cho con hết

Đắng cay chỉ mẹ biết

Nhắc nhở chỉ mẹ hay.

Mẹ lo đữa, lo ngừng

Mẹ bếp lửa tối ngày

Khi con đau con ốm

Mẹ như mặt trời sớm

Hôn giác ngủ của con

Suổi ấm con đông tối

Mẹ là quá máu mất rồi

(Hoàng Thị Minh Khanh)

Bài Tập Đọc Số 8

Sói Và Sóc

Một hôm, Sóc đang loanh quanh chuyện cành vui chơi. Bỗng may bị húc chân, Sóc rơi xuống trúng đầu một con sói đang nằm ngủ dưới gốc cây. Sói dậy mình tính dạy. Nó chộp được Sóc. Nó vừa dạy mắt vừa cười và nó nói: “Thế là ta được miếng mới ngon!”

Sóc khoanh tay xin Sói tha cho mình. Nghe Sóc xin tha, Sói tầm tì củng cươi, nó nói:

– Muốn được tha à, hãy trả lời ta câu này: Tại sao, ta lúc nào cũng buồn bực, còn lũ Sóc nhà ngươi thì lúc nào cũng vui đùa nhảy nhót?

Sóc lệch phép nó nói:

– Thưa bác Sói, bác hãy thả tôi ra, tôi sẽ nói rõ điều bí mật đó cho bác rõ. Nghe Sóc nói, Sói thả Sóc ra. Sóc vội trèo tốt lên ngọn cây, rồi thỏ phao nhảy nhót.

(Truyền ngụ ngôn)

Bài Tập Đọc Số 9

Trí Khôn

Một hôm, nom thấy bác thợ cấy bảo gì trâu phải nghe, Cấp lắm lấy làm lạ hỏi:

– Này, Trâu kia, mày to xác như thế này sao dại thế, sao lại để cho bác ta sai khiến như thế?

– Bác ấy có trí khôn.

Cấp ngạc nhiên quay sang bác thợ cấy:

– Này bác, trí khôn của bác để ở đâu?

– Ta để ở nhà.

– Bác vời, Cấp ăn mắt Trâu của ta thì sao? Có thuần cho ta cắt vỏ cây kia thì ta vời lấy cho mày xem!

Cấp muốn xem, nên thuần ngay. Sau khi Cấp bị cắt chất vỏ cây vào góc cây, bác nông dân lấy búa cây phang cho nó một trận nên thân. Vừa phang bác vừa nói:

– Trí khôn của ta đây! Trí khôn của ta đây!

(Truyền ngụ ngôn)

Bài Tập Đọc Số 10

Sự Từ Và Sóc

Một con sóc muốn quyết định đấu với sự từ nhiên một ngày đẹp trời. Sự từ lẫn lộn thử tháng tháng. Sóc khiêu khích: “Sự từ hùng mạnh như người mà lại sợ ta?”

Sự từ thông thả trả lời: “Dẫu kết quả trận đấu có ra sao đi nữa, sau này muốn thú sẽ biết đến người như kẻ đã dám thách thức với Chúa tể sơn lâm. Còn ta suốt đời sẽ mang danh tên Chúa tể sơn lâm lại luôn võ với hàng sóc chồn tiêu nguyện biết!”

(Nguồn: Internet)

Bài Tập Đọc Số 11

Màu Sắc

Mẹ dạy con bài học về màu

Bài đầu tiên chỉ có xanh và đỏ

Màu lá và xanh là quả

Sắc màu nào cũng rõ cũng tươi

Mắt ngày thơ, trong trẻo, yêu đời

Con chỉ thích những màu sắc sởi

Áo con mặc cũng vàng hơn hở

Cháy trong nhành như một chú gà con…

(Anh Thư)

Bài Tập Đọc Số 12

Cú Và Chim Gáy

Một con chim Gáy gặp một con Cú Mèo.

Chim Gáy hỏi:

– Chị định đi đâu đó?

Cú Mèo nó nói:

– Tôi sắp đi sang ở bên hướng đồng rồi.

Chim Gáy liền hỏi:

– Tại sao chị phải ra đi?

Cú Mèo trả lời:

– Ở đây, thiên hạ ghét tiếng kêu của tôi, nên tôi phải tìm đường sang bên ấy.

Chim Gáy lại nói:

– Hay là chị có thể đổi tiếng kêu của mình được không? Chị biết đấy, không đổi tiếng kêu thì sang bên ấy, thiên hạ nghe tiếng kêu của chị cũng lại ghét bẩn mà thôi. Đâu cũng vậy mà!

Cứ như ý chị, chỉ bằng tôi rút cánh lại, thu cánh lại im lặng suốt đời là khổ!

(Truyền ngụ ngôn)

Bài Tập Đọc Số 13

Cảnh Về Đêm

Cuối ngày, những tia nắng cuối cùng cũng dần biến mất, màn đêm bắt đầu buông xuống bao trùm cả thành phố. Những ngọn đèn được bật lên, tỏa sáng tựa như những vì sao trên bầu trời. Trên bầu trời, trăng tròn lơ lửng, hồng hồng, trăng tròn và sáng tỏ hơn.

Dưới lòng thị người có kính cận của đàn Ngọc Sơn, cầu Thê Húc… ai cũng choáng ngợp bởi nét đẹp của đô thị sầm uất. Những tòa nhà cao tầng đổ bóng lên ánh sáng sớm lén sát nhau. Ánh đèn đường, đèn điện trong nhà được thắp lên tạo thành những tia sáng lung linh, xua tan màn đêm tối tăm. Hàng cây xanh trên bậc vỉa hè cũng được thay màu áo mới. Những dãy đèn đủ màu liên tục chớp nhảy trông thật đã mắt.

(Nguồn: Internet)

Bài Tập Đọc Lớp 1 Số 14

Hè Về

Đàn chim se sẩy

Hót trên cánh đồng

Bạn ơi biết không

Hè về rồi đó

Chiều nay bạn gió

Mang nón về đây

Một chuyện đò qua

Ôi mới đẹp thay!

Phương hướng mở mắt

Dòng sông trong vắt

Trước lên bãi xa

Mang theo lũ bướm

Cánh diệu bay lượn

Thênh thang lúa đồng

Bạn ơi thích không?

Hè về rồi đó!

(Nguyễn Lãm Thắng)

Bài Tập Đọc Số 15

Bé làm hóa sĩ

Bé muốn làm hóa sĩ

Để vẽ ông mắt trời

Với những tia nắng ấm

Sáng rực khắp muôn nơi

Bé thích làm hóa sĩ

Để vẽ cô và mẹ

Mẹ có đôi mắt tròn

Còn cô cửu thật tươi

Bé ước làm hóa sĩ

Để vẽ bạn, vẽ trường

Vẽ những gì yêu thích

Đắm hình trên tranh bé.

(Tạ Minh Thùy)

Hy vọng rằng những bài tập đọc trên đây sẽ giúp bé nâng cao kỹ năng đọc diễn cảm, mở rộng vốn từ và yêu thích việc học Tiếng Việt hơn.

Các bài đọc trên đều có sẵn trong cuốn Bài Tập Bổ Trợ Nâng Cao Tiếng Việt Lớp 1 – Tập 2 và cuốn 50 Đề Tăng Điểm Nhanh Tiếng Việt Lớp 1. Bố mẹ hãy mua hai cuốn sách này để giúp con học tốt môn Tiếng Việt hơn nhé!

Link đọc thử sách Bài Tập Bổ Trợ Nâng Cao Tiếng Việt Lớp 1 – Tập 2: https://drive.google.com/file/d/1N-ztVhE1Q-KMJqS4io68wR_JJuCVq2Fd/view

Link đọc thử sách 50 Đề Tăng Điểm Nhanh Tiếng Việt Lớp 1: https://drive.google.com/file/d/1tsbA245zeOJAh5zcTr9H43LdoCzHOlNm/view

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 1 hàng đầu tại Việt Nam!

Tkbooks.vn

Trong quá trình học tập, việc rèn luyện kỹ năng toán học cho trẻ em là rất quan trọng. Chúng tôi rất vui mừng giới thiệu đến quý phụ huynh và học sinh tài liệu “Bài tập so sánh số có hai chữ số lớp 1” – một nguồn tài liệu bổ ích và thú vị, giúp các em làm quen với các bài toán thú vị, đồng thời phát triển tư duy toán học một cách tự nhiên.

I. Bài tập so sánh các số có hai chữ số

Tài liệu này bao gồm nhiều bài tập thiết thực, giúp học sinh lớp 1 vận dụng lý thuyết vào thực tế thông qua việc so sánh các số có hai chữ số. Việc tiếp cận bài toán có hệ thống giúp các em không chỉ nắm vững kiến thức mà còn phát triển khả năng phân tích và tư duy logic.

Bài tập so sánh số có hai chữ số – File 1

Có nhiều bài tập được thiết kế khéo léo, từ dễ đến khó, giúp các em vừa học vừa chơi. Việc so sánh các số không chỉ giúp các em rèn luyện kỹ năng số học mà còn phát triển khả năng tư duy phản biện.

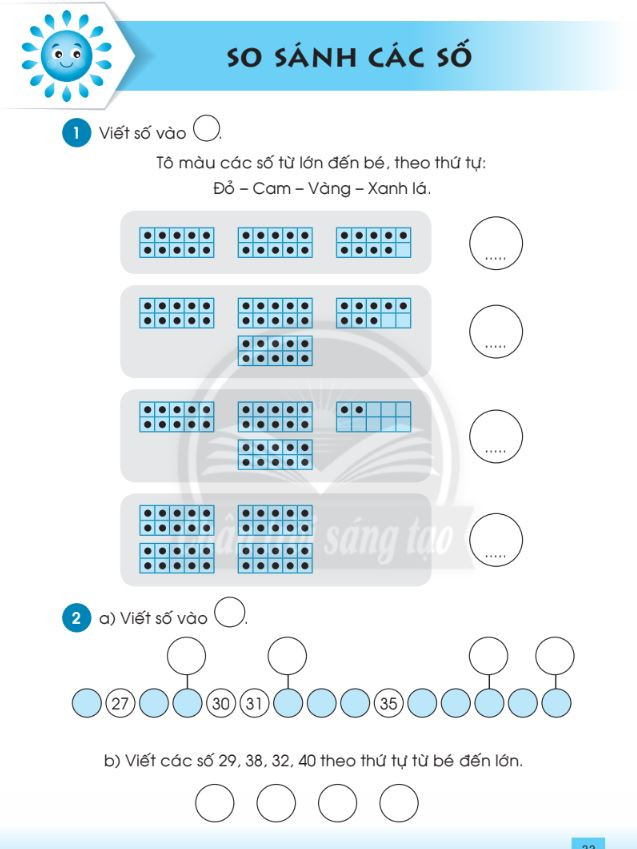
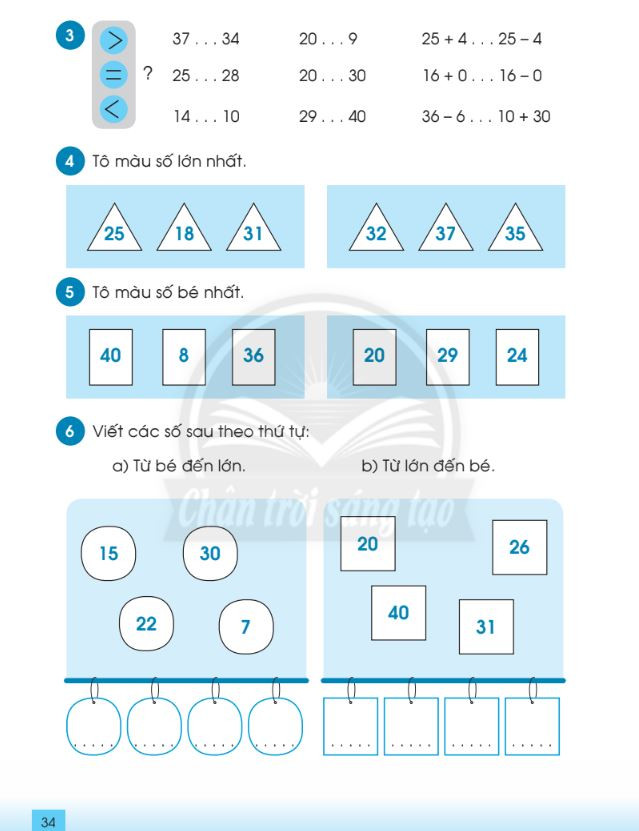Bài tập so sánh số có hai chữ số – File 2

II. Bài tập luyện tập chung

Ngoài các bài tập so sánh, tài liệu còn cung cấp những bài tập tổng hợp giúp các em củng cố lại những kiến thức đã học. Những bài tập này không chỉ giúp ôn luyện mà còn khám phá thêm nhiều kiến thức mới trong toán học.

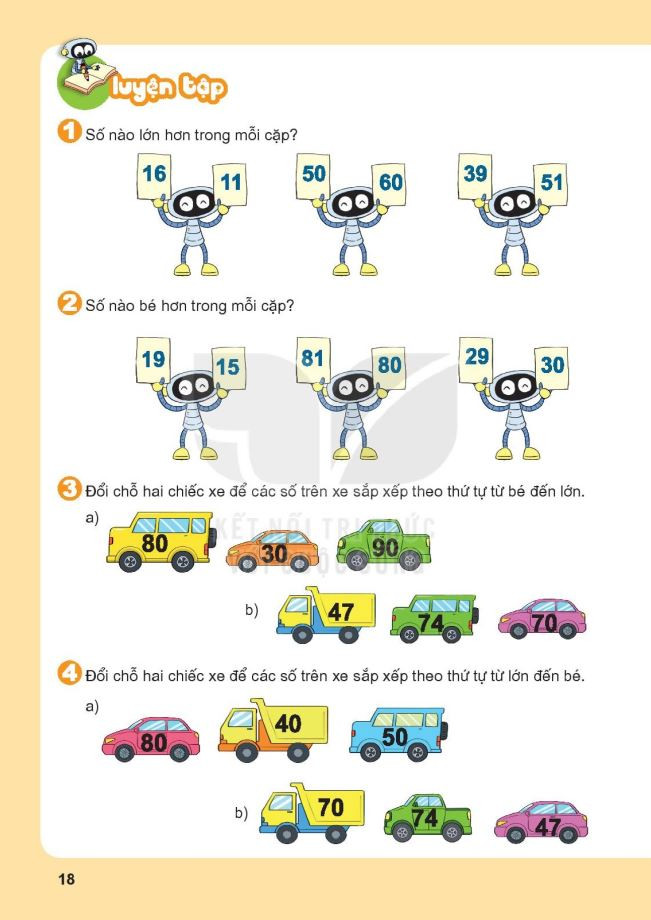Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 1

Các bài tập này được xây dựng với cấu trúc rõ ràng, dễ hiểu, phù hợp với khả năng tiếp thu của học sinh lớp 1, từ đó giúp các em phần nào tự tin hơn trong việc giải quyết các bài toán trong tương lai.

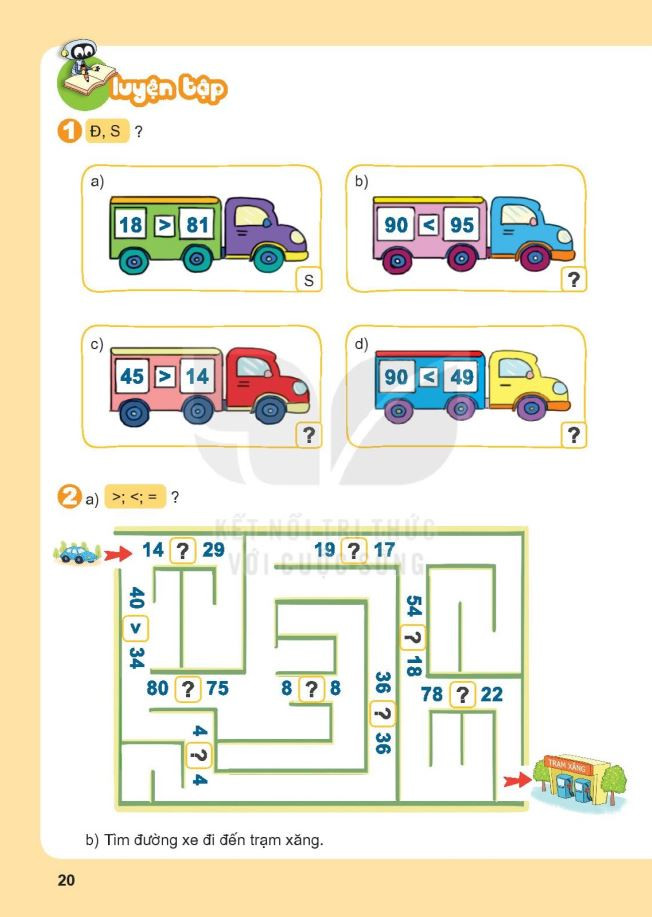Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 2

Chúng tôi hy vọng tài liệu “Bài tập so sánh số có hai chữ số lớp 1” sẽ trở thành người bạn đồng hành trong quá trình học tập của các em, mang đến cho các em những trải nghiệm học tập thú vị và hiệu quả.

Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 3

Đừng quên tải tài liệu PDF miễn phí từ TKbooks.vn và bắt đầu hành trình luyện tập ngay hôm nay. Tài liệu này sẽ giúp các em có được sự chuẩn bị tốt nhất cho những năm học tiếp theo.

*>>> Tải file bài tập PDF miễn phí tại đây*!

Ngoài các bài tập được giới thiệu trên, các bậc phụ huynh có thể tham khảo thêm các tài liệu khác như:

• Bài tập bổ trợ nâng cao Toán lớp 1 – Tập 1
• 50 đề tăng điểm nhanh Toán lớp 1

Hy vọng rằng những tài liệu này sẽ cung cấp thêm nhiều kiến thức bổ ích cho các em học sinh lớp 1. Hãy cùng chúng tôi phát triển tư duy toán học ngay từ bây giờ để các em tự tin hơn trong tương lai.

TKbooks.vn

Học tiếng Trung là một thử thách lớn nếu bạn chưa tìm ra phương pháp hiệu quả. Tuy nhiên, qua thời gian và nỗ lực, bạn sẽ phát hiện ra rằng việc học ngôn ngữ này không chỉ mang lại kỹ năng giao tiếp mà còn mở ra nhiều cơ hội mới trong công việc và cuộc sống. Để giúp bạn bước vào hành trình này, bài viết này sẽ điểm qua một số cuốn sách hữu ích dành cho những ai mới bắt đầu học tiếng Trung và cung cấp những phương pháp học tập hiệu quả.

1. Cuốn sách “Tự học tiếng Trung cho người mới bắt đầu”

Cuốn sách Tự học tiếng Trung cho người mới bắt đầu là sự lựa chọn tuyệt vời cho những ai đang tìm kiếm nền tảng kiến thức cơ bản về tiếng Trung. Cuốn sách tổng hợp những kiến thức quan trọng nhất về ngữ pháp, từ vựng và phát âm, giúp người học dễ dàng tiếp cận và nắm bắt.

Tự học tiếng Trung cho người mới bắt đầu

Chương trình học được chia thành nhiều bài học phong phú, bao gồm các chủ đề như hội thoại, từ vựng thông dụng, cùng với giải thích chi tiết về ngữ pháp. Cuốn sách cung cấp bản dịch dễ hiểu cùng các ví dụ thực tế, rất thiết thực cho việc giao tiếp hàng ngày.

Đồng thời, cuốn sách cũng giúp bạn xây dựng tự tin để nghiên cứu sâu hơn về ngôn ngữ thú vị này.

2. Cuốn sách “Tự học tiếng Trung dành cho người Việt”

Nếu bạn là người Việt đang muốn học tiếng Trung, cuốn sách Tự học tiếng Trung dành cho người Việt sẽ là lựa chọn phù hợp. Sách được thiết kế đặc biệt dành cho người Việt với những bài học phù hợp với trình độ sơ cấp.

Tự học tiếng Trung dành cho người Việt

Cuốn sách bao gồm các bài học từ cơ bản đến nâng cao, giúp người học nắm vững cách phát âm, từ vựng và phù hợp với văn hóa giao tiếp của người Trung Quốc. Thông qua việc luyện nghe, xem phim, và tham gia các hoạt động giao tiếp, bạn sẽ dần quen với ngôn ngữ này.

3. Cuốn sách “Tự học nhanh tiếng phổ thông Trung Hoa”

Cuốn sách Tự học nhanh tiếng phổ thông Trung Hoa là tài liệu lý tưởng dành cho những ai muốn nâng cao khả năng giao tiếp một cách nhanh chóng.

Cuốn sách này chia thành nhiều phần, mỗi phần tập trung vào các tình huống giao tiếp khác nhau, từ mua sắm, ẩm thực, đến các chủ đề hàng ngày. Điều này giúp bạn trang bị vốn từ vựng phong phú và cải thiện khả năng ứng dụng trong cuộc sống thực tế.

Kết luận

Học tiếng Trung là một hành trình thú vị nhưng đầy thử thách. Các cuốn sách như “Tự học tiếng Trung cho người mới bắt đầu”, “Tự học tiếng Trung dành cho người Việt”, và “Tự học nhanh tiếng phổ thông Trung Hoa” không chỉ cung cấp kiến thức cơ bản mà còn giúp bạn tạo dựng nền tảng vững chắc cho quá trình học tập. Hãy kiên trì và tìm phương pháp học phù hợp với mình để nhanh chóng thành thạo tiếng Trung.

Để có thêm nhiều thông tin và phương pháp học tập hữu ích, hãy truy cập loigiaihay.edu.vn và cùng khám phá thế giới tiếng Trung nhé!

Trong chương trình Toán lớp 9, việc chứng minh tứ giác nội tiếp là một phần quan trọng giúp học sinh nắm vững kiến thức về hình học và phát triển tư duy logic. Bài viết này sẽ hướng dẫn các em cách chứng minh tứ giác nội tiếp một cách chi tiết và dễ hiểu thông qua lý thuyết, ví dụ cụ thể cùng những bài tập kèm lời giải để các em có thể tham khảo.

I. Lý Thuyết Về Tứ Giác Nội Tiếp

1. Khái Niệm Tứ Giác Nội Tiếp

Tứ giác nội tiếp là một tứ giác có bốn đỉnh nằm trên một đường tròn. Trong đó, tổng số đo hai góc đối diện của tứ giác luôn bằng 180 độ.

a. Tính Chất

• Định lý 1: Một tứ giác được gọi là nội tiếp khi và chỉ khi tổng số đo hai góc đối diện bằng 180°.
• Định lý 2: Nếu một tứ giác có hai góc ở cùng một phía so với một cạnh, và cùng nhìn cạnh đó với một góc α, thì tứ giác đó là tứ giác nội tiếp.

Định lý 2 về tứ giác nội tiếp

Ví dụ: Tứ giác ABCD như hình dưới đây có góc ABD = góc ACD thì tứ giác này là tứ giác nội tiếp.

b. Cách Chứng Minh Tứ Giác Nội Tiếp

Để chứng minh một tứ giác là nội tiếp, ta cần chứng minh rằng tứ giác đó có tổng hai góc đối diện bằng 180 độ.

• Nếu ta có một tứ giác là nội tiếp, thì tổng số đo hai góc đối diện bằng 180°.
• Ngược lại, nếu tổng hai góc đối diện bằng 180°, ta có thể suy ra đó là tứ giác nội tiếp.

c. Ví Dụ

Trong hình vẽ tứ giác ABCD là tứ giác nội tiếp.

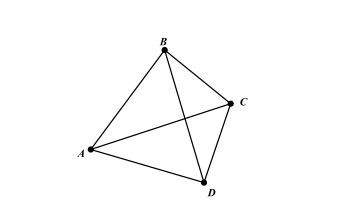
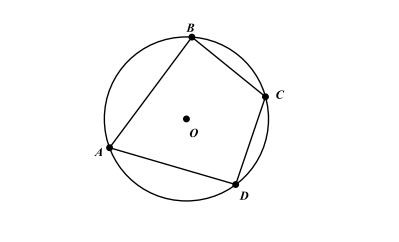Ví dụ về tứ giác nội tiếp

Góc BAD và BCD là hai góc đối diện nên ta có BAD + BCD = 180°.

II. Các Bài Toán Chứng Minh Tứ Giác Nội Tiếp Lớp 9

Bài 1:

Cho tam giác ABC nội tiếp đường tròn (O). Đường thẳng song song với tiếp tuyến tại C cắt các cạnh AC, BC lần lượt tại D, E. Chứng minh rằng tứ giác ABED nội tiếp.

Giải:

Gọi Cx là tia tiếp tuyến tại O (tia Cx nằm trên nửa mặt phẳng không chứa B). Ta có góc ACx = góc ABC, mà góc ACx = góc EDC nên góc ABC = góc EDC.

Vậy tứ giác ABED là tứ giác nội tiếp.

Bài 2:

Cho tam giác ABC nội tiếp đường tròn (O). Vẽ dây DE vuông góc với OA cắt các cạnh AB, AC lần lượt tại S, K.

Chứng minh rằng: tứ giác BCKS nội tiếp.

Hình vẽ minh họa bài 2

Giải:

OA ⊥ DE (gt) ⇒ góc xAC = góc AED

⇒ AD = AE

Góc BSK = (số đo cung BCE + số đo cung AD)/2 (góc có 2 đỉnh ở bên trong đường tròn).

Góc BSK = số đo cung AB/2 (góc nội tiếp).

Do đó: góc BSK + góc BCK = (số đo cung BCE + số đo cung AD + số đo cung AB)/2

= (số đo cung BCE + số đo cung AE + số đo cung AB)/2 = 360°/2 = 180°

⇒ Tứ giác nội tiếp BCKS.

Bài 3:

Cho tam giác nhọn ABC. Đường tròn đường kính BC cắt AB và AC theo thứ tự tại D và E. Gọi H là giao điểm của BE và CD, tia AH cắt BC tại F. Số tứ giác nội tiếp được đương tròn có trong hình vẽ là bao nhiêu?

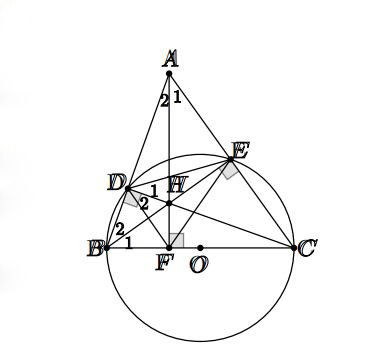Hình vẽ minh họa bài 3

Giải:

Ta có tam giác BDC vuông tại D và tam giác BEC vuông tại E vì hai tam giác này nội tiếp được đường tròn (O) đường kính BC.

BE và CD là hai đường cao của ABC nên H là trực tâm của tam giác này.

⇒ AH ⊥ BC tại F (vì AH là đường cao thứ ba).

Từ đó ta có:

• Ba tứ giác AEDH; BDHF; CEHF nội tiếp được vì có hai góc đối diện bù nhau.
• Ba tứ giác AEFB; BDEC; ADFC nội tiếp được vì có hai đỉnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc 90°.

Vậy trong hình vẽ có tất cả 6 tứ giác nội tiếp được đường tròn.

Bài 4:

Cho tam giác ABC nội tiếp đường tròn (O). Vẽ Ax là tiếp tuyến của đường tròn (O). Đường thẳng song song với A cắt các cạnh AB, AC lần lượt tại D, E.

Chứng minh rằng tứ giác BCED nội tiếp.

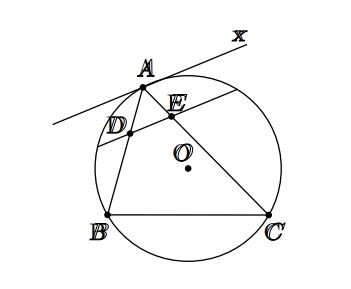Hình vẽ minh họa bài 4

Giải:

Ta có Ax // DE (giả thiết)

⇒ Góc xAC = góc AED (hệ quả của góc tạo bởi tia tiếp tuyến dây cung)

Do đó: góc AED = góc DBC

Suy ra tứ giác BCED là tứ giác nội tiếp.

Bài 5:

Cho tam giác ABC cân tại A, nội tiếp trong đường tròn (O) đường kính là AI. Gọi E là trung điểm AB và K là trung điểm của OI.

a) Chứng minh tam giác EKB là tam giác cân.

b) Chứng minh tứ giác AEKC là một tứ giác nội tiếp.

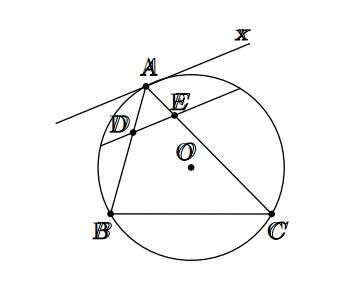Hình vẽ minh họa bài 5

Giải:

a) Gọi H là trung điểm của đoạn thẳng BE.

Ta có: E là trung điểm AB, AB không qua O (gt). Mà góc ABI = 90° (góc nội tiếp chắn ngoài đường tròn).

Vì OE ⊥ AB, BI ⊥ AB (góc ABI = 90°) ⇒ OE // BI.

Do đó tứ giác BEOI là hình thang.

Mà H, K lần lượt là trung điểm các cạnh BE, OI nên HK // OE.

Ta có: HK // OE, OE ⊥ AB ⇒ HK ⊥ AB

Tam giác EKB có HK vừa là đường cao vừa là đường trung tuyến ⇒ tam giác EKB cân tại K.

b) OB = OC (= R) và AB = AC (gt)

⇒ O và A thuộc đường trung trực của đoạn thẳng BC.

⇒ OA là đường trung trực của đoạn thẳng BC.

Mà K ∈ OA nên KB = KC

Xét tam giác KBA và tam giác ICA có: AB = AC (gt)

KB = KC; AK là cạnh chung

Do đó: tam giác KBA = tam giác RCA (c.c.c)

⇒ Góc KBA = góc KCA ⇒ góc KBA = góc KEB (tam giác EKB cân).

Do đó: góc KEB = góc KCA ⇒ Tứ giác AEKC nội tiếp được.

Việc nắm vững cách chứng minh tứ giác nội tiếp lớp 9 không chỉ giúp các em học tốt môn Toán mà còn giúp các em đạt điểm cao hơn trong kỳ thi tuyển sinh vào 10 sắp tới.

Hy vọng qua bài viết này, các em sẽ có thể tự tin hơn khi đối mặt với các bài toán liên quan đến tứ giác nội tiếp. Đừng quên tham khảo thêm 2 cuốn Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số và Hình học để biết cách giải tất cả các bài toán trong chương trình lớp 9 nhé!

Link để tham khảo phần Đại số: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view

Link để tham khảo phần Hình học: https://drive.google.com/file/d/162Yv0A_lC8XmgSN_AjwxVuKPWpbVVkJj/view

Nếu các em có bất kỳ thắc mắc nào, hãy để lại bình luận dưới bài viết để được giải đáp nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 9 hàng đầu tại Việt Nam!

Trong bài viết này, chúng tôi sẽ cung cấp thông tin chi tiết về các đề thi và đáp án cho kỳ thi vào lớp 10 môn Toán năm học 2025 – 2026. Những tài liệu này được tổng hợp từ nhiều trường uy tín như THCS & THPT Nguyễn Tất Thành, Đại học Sư phạm Hà Nội, và một số trường khác ở Nghệ An. Đây sẽ là nguồn tài liệu quý giá giúp các em học sinh làm quen với dạng bài, rèn luyện kỹ năng giải đề và nâng cao khả năng làm bài thi.

I. Đề Thi Vào Lớp 10 Trường THCS & THPT Nguyễn Tất Thành

1. Đề Thi

Mã Đề 901

Đề thi vào lớp 10 môn Toán năm học 2025 – 2026 – File số 1

Đề thi vào lớp 10 môn Toán năm học 2025 – 2026 – File số 2

Mã Đề 902

Đề thi vào lớp 10 môn Toán năm học 2025 – 2026 – Mã đề 902 – File số 1

Đề thi vào lớp 10 môn Toán năm học 2025 – 2026 – Mã đề 902 – File số 2

Tải file đề thi và đáp án vào lớp 10 trường THCS & THPT Nguyễn Tất Thành, Đại học Sư phạm Hà Nội dưới dạng PDF miễn phí tại đây!

2. Đáp Án

Mã Đề 901

Đáp án mã đề thi 901 – File số 1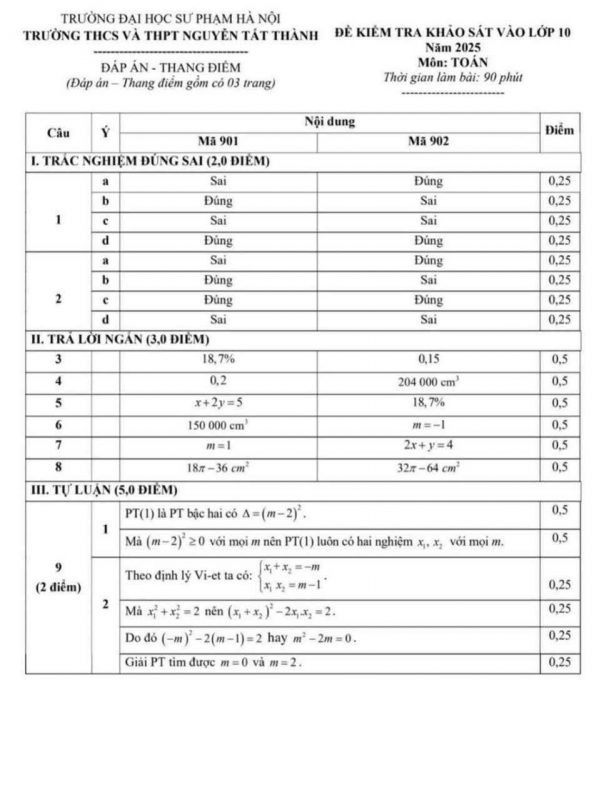

Đáp án mã đề thi 901 – File số 2

Mã Đề 902

Đáp án mã đề 902 – File số 1

Đáp án mã đề 902 – File số 2

II. Đề Thi và Đáp Án Vào Lớp 10 THPT Tỉnh Nghệ An

1. Đề Thi

Đề thi vào 10 môn Toán tỉnh Nghệ An năm học 2025 – 2026 – File số 1

Đề thi vào 10 môn Toán tỉnh Nghệ An năm học 2025 – 2026 – File số 2

Tải file đề thi và đáp án vào lớp 10 THPT năm học 2025 – 2026 theo cấu trúc đề thi chính thức Tỉnh Nghệ An dưới dạng PDF miễn phí tại đây!

2. Đáp Án

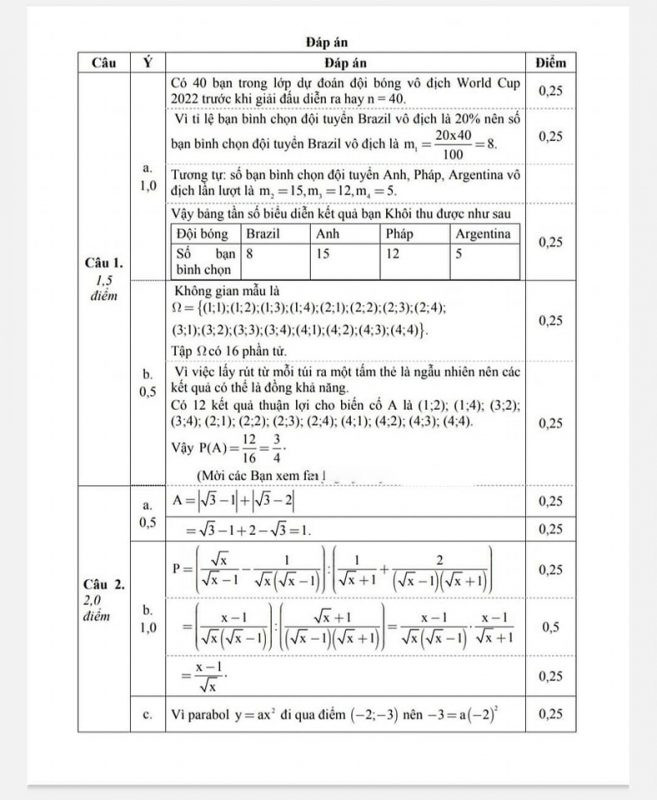Đáp án đề thi Toán vào 10 tỉnh Nghệ An – File số 1

Đáp án đề thi Toán vào 10 tỉnh Nghệ An – File số 2

Đáp án đề thi Toán vào 10 tỉnh Nghệ An – File số 3

III. Đề Thi và Đáp Án Vào Lớp 10 Trường THCS Nguyễn Hồng Lê – Sầm Sơn

1. Đề Thi

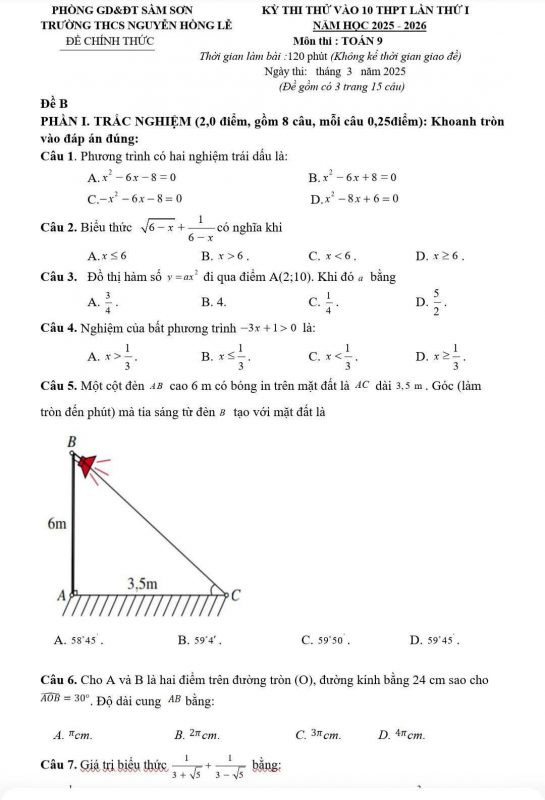Đề thi Toán vào 10 trường THCS Nguyễn Hồng Lê – File số 1

Đề thi Toán vào 10 trường THCS Nguyễn Hồng Lê – File số 2

Tải đề thi và đáp án vào lớp 10 trường THCS Nguyễn Hồng Lê – Sầm Sơn dưới dạng PDF miễn phí tại đây!

2. Đáp Án

Đáp án đề thi môn Toán vào 10 trường Nguyễn Hồng Lê – File 1

Đáp án đề thi môn Toán vào 10 trường Nguyễn Hồng Lê – File 2

Đáp án đề thi môn Toán vào 10 trường Nguyễn Hồng Lê – File 3

Đáp án đề thi môn Toán vào 10 trường Nguyễn Hồng Lê – File 4

IV. Đề Thi và Đáp Án Vào Lớp 10 THPT Chuyên Đại học Sư Phạm Năm 2025

1. Đề Thi

Đề thi vào lớp 10 năm học 2025 – 2026 trường chuyên Đại học Sư Phạm

Tải file đề thi và đáp án vào lớp 10 THPT chuyên Đại học Sư Phạm năm 2025 dưới dạng PDF miễn phí tại đây!

2. Đáp Án

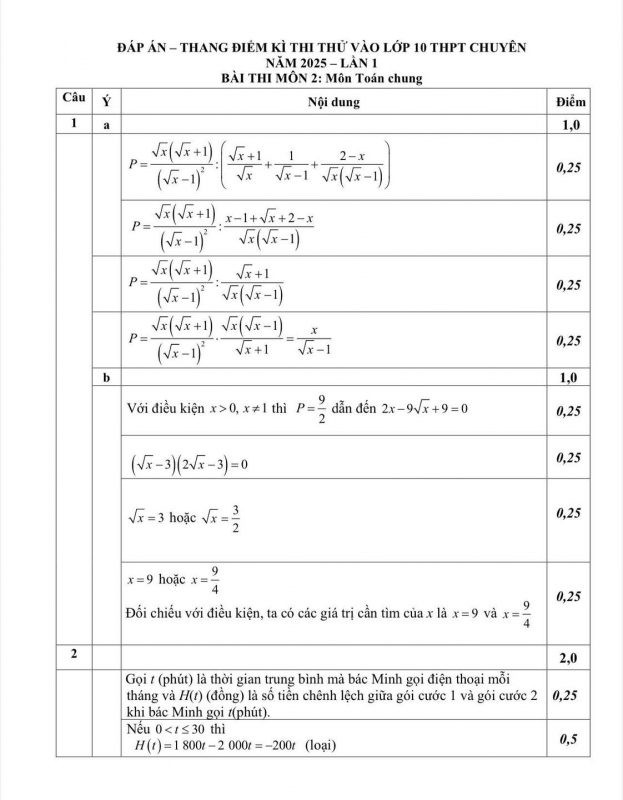Đáp án – File số 1

Đáp án – File số 2

Đáp án – File số 3

Đáp án – File số 4

Đáp án – File số 5

V. Đề Thi và Đáp Án Vào Lớp 10 Môn Toán Năm Học 2025 – 2026 Huyện Nghi Xuân

1. Đề Thi

File đề thi số 1

File đề thi số 2

2. Đáp Án

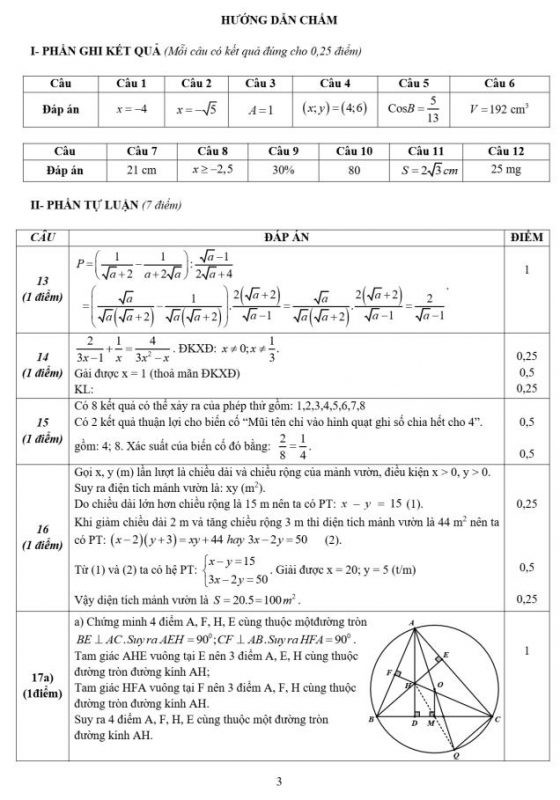File đáp án số 1

File đáp án số 2

Những tài liệu về đề thi và đáp án vào lớp 10 môn Toán năm 2025 – 2026 kèm đáp án chi tiết trên đã giúp các em học sinh có thêm nguồn tham khảo hữu ích, rèn luyện kỹ năng làm bài và chuẩn bị tốt nhất cho kỳ thi sắp tới.

Để nâng cao khả năng tư duy Toán học và chuẩn bị cho kỳ thi vào lớp 10, các em có thể tham khảo bộ sách “Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 9 – Luyện thi vào 10” của Tkbooks. Đây là tài liệu tổng hợp kiến thức theo sơ đồ tư duy, sẽ giúp học sinh nắm vững lý thuyết và áp dụng linh hoạt vào bài thi.

• Phần Đại số: Xem chi tiết

• Phần Hình học và Xác suất: Xem chi tiết

Chúc các em học tốt và đạt kết quả cao trong kỳ thi sắp tới!