Trong hành trình học tập của trẻ, việc lựa chọn sách tham khảo phù hợp đóng vai trò rất quan trọng để phát triển ngôn ngữ, tư duy và kỹ năng sáng tạo. Đặc biệt, với chương trình học Tiếng Việt lớp 4, những cuốn sách tham khảo sẽ đồng hành cùng các em trong việc củng cố kiến thức và nâng cao khả năng sử dụng ngôn ngữ. Bài viết này sẽ giới thiệu đến quý phụ huynh những cuốn sách tham khảo Tiếng Việt lớp 4 tốt nhất mà các em nên sở hữu.
1. 50 Đề Tăng Điểm Nhanh Tiếng Việt Lớp 4
Cuốn sách 50 Đề Tăng Điểm Nhanh Tiếng Việt 4 được biên soạn theo chương trình giáo dục phổ thông hiện hành. Những đề kiểm tra bao gồm nội dung kiến thức liên quan đến từng tuần học trong sách giáo khoa Tiếng Việt 4, giúp các em nắm vững kiến thức một cách có hệ thống.
Mỗi đề kiểm tra không chỉ giúp các em làm quen với kiểu câu hỏi mà còn củng cố khả năng đọc hiểu, giao tiếp và viết văn. Cuốn sách không chỉ đơn thuần là một công cụ ôn tập, mà còn là người bạn đồng hành giúp các em yêu thích môn Tiếng Việt nhiều hơn.
 Cuốn sách 50 Đề Tăng Điểm Nhanh Tiếng Việt Lớp 4
Cuốn sách 50 Đề Tăng Điểm Nhanh Tiếng Việt Lớp 4
Nội dung cuốn sách
Cuốn sách được chia thành 3 phần chính: Đọc hiểu, Luyện từ và câu, Viết. Mỗi phần sẽ là những bài học được biên soạn bám sát với nội dung sách giáo khoa, giúp các em nâng cao kỹ năng sử dụng ngôn ngữ trong các tình huống thực tế. Nội dung phong phú, đa dạng và gần gũi với đời sống sẽ giúp các em phát triển kỹ năng quan sát và lựa chọn từ ngữ một cách thuần thục.
Ưu điểm của cuốn sách
- Học nhanh, dễ dàng đạt điểm cao
- Củng cố vững kiến thức ngữ pháp
- Cải thiện khả năng viết và trình bày bài văn
- Giúp các em tự tin hơn trong các kỳ thi
Đọc thử sách: https://drive.google.com/file/d/10tIpcwExHo4NVPBLRL6RqmdqFvY11e_j/view
2. Bài Tập Bổ Trợ Nâng Cao Tiếng Việt Lớp 4
Bộ sách Bài Tập Bổ Trợ Nâng Cao Tiếng Việt 4 với nội dung được biên soạn theo chương trình GDPT 2018 sẽ giúp các em rèn luyện kỹ năng đọc hiểu và nắm vững quy tắc chính tả. Các bài tập có cấu trúc từ dễ đến khó, phù hợp với trình độ và nhu cầu học tập của học sinh.
 Bộ sách bài tập bổ trợ nâng cao tiếng việt lớp 4
Bộ sách bài tập bổ trợ nâng cao tiếng việt lớp 4
Nội dung cuốn sách
Cuốn sách chia thành 2 tập, mỗi tập là hệ thống bài tập giúp các em củng cố kiến thức theo tuần. Những bài học này không chỉ giúp giải quyết nhanh các bài kiểm tra mà còn tạo nền tảng kiến thức vững chắc cho các em trong cách diễn đạt và viết văn.
Ưu điểm nổi bật của cuốn sách
- Hơn 220 bài toán luyện tập,đáp án giải chi tiết
- Giúp các em hiểu bài một cách dễ dàng hơn
- Tổng hợp kiến thức theo đúng nội dung sách giáo khoa
Ưu điểm đặc biệt của cuốn sách
Với mỗi bài học, các em sẽ được khám phá những bài thơ, bài văn hay và có ý nghĩa. Từ đó phát triển cảm xúc và tình cảm tốt đẹp cho các em.
Đọc thử sách: https://drive.google.com/file/d/1E_72gqGrCDsEOyVYOhA8Z8ltAqU6lhqu/view
3. Chinh Phục Nâng Cao Tiếng Việt 4
Cuốn sách Chinh Phục Nâng Cao Tiếng Việt 4 với gần 600 câu hỏi trắc nghiệm giúp học sinh củng cố kiến thức Tiếng Việt một cách vững vàng nhất. Nội dung sát với chương trình học, phù hợp cho những em có nhu cầu nâng cao hơn.
 Sách Chinh Phục Nâng Cao Tiếng Việt lớp 4
Sách Chinh Phục Nâng Cao Tiếng Việt lớp 4
Nội dung cuốn sách
Cuốn sách bao gồm 5 đề kiểm tra giữa kì và 15 đề kiểm tra cuối kì với nội dung phong phú, bám sát chương trình học hiện hành. Mỗi đề gồm có phần đọc, hiểu và lựa chọn đáp án (trắc nghiệm), phần sau là bài tập áp dụng với hình ảnh sinh động, thú vị.
Ưu điểm của cuốn sách
- Nội dung học phong phú, bám sát chương trình
- Bài tập đa dạng và sinh động giúp tránh nhàm chán
- Sách được in bằng giấy trắng không lóa mắt, chất lượng cao
4. Đề Kiểm Tra Tiếng Việt Lớp 4
Cuốn sách Đề Kiểm Tra Tiếng Việt 4 cung cấp 5 đề kiểm tra giữa kì và 15 đề kiểm tra cuối kì, giúp học sinh làm quen với cấu trúc đề thi mà giáo viên xây dựng. Nội dung được thiết kế đơn giản nhưng hiệu quả, giúp các em ôn tập hiệu quả hơn.
 Bộ sách Đề Kiểm Tra Tiếng Việt lớp 4
Bộ sách Đề Kiểm Tra Tiếng Việt lớp 4
Nội dung cuốn sách
Cuốn sách bao gồm nội dung kiểm tra chú trọng đến khả năng đọc hiểu và viết, giúp học sinh làm quen với các dạng bài tập khác nhau. Mỗi đề kiểm tra đều có nội dung độc đáo, giúp các em cảm nhận giai điệu của văn học qua từng câu chữ.
Ưu điểm của cuốn sách
- Nội dung đặc sắc, bám sát chương trình học
- Bài tập đa dạng, phong phú giúp các em không cảm thấy nhàm chán
- Sách được in bằng giấy chất lượng, dễ viết và học tập
5. Bồi Dưỡng Tiếng Việt Lớp 4
Cuốn sách Bồi Dưỡng Tiếng Việt Lớp 4 sẽ giúp trẻ học tốt môn Tiếng Việt theo chương trình mới, đồng thời phát triển kỹ năng giao tiếp và tư duy phản biện.
 Sách Bồi Dưỡng Tiếng Việt lớp 4
Sách Bồi Dưỡng Tiếng Việt lớp 4
Nội dung cuốn sách
Cuốn sách tập trung vào việc hình thành và phát triển kỹ năng sử dụng Tiếng Việt cho các em thông qua các trải nghiệm thực tế. Học sinh sẽ được tiếp cận với những kiến thức cơ bản và nâng cao, cùng với việc nghe, nói, đọc, viết một cách thuần thục.
Ưu điểm của cuốn sách
- Cung cấp kiến thức về tự nhiên và xã hội một cách tự nhiên
- Hình thành thói quen chăm sóc văn hóa và ngôn ngữ Tiếng Việt
- Tương tác thân thiện, giúp trẻ phát triển tình yêu với văn học
Những cuốn sách này không chỉ đơn thuần là tài liệu học tập mà còn là nguồn cảm hứng, khích lệ các em yêu thích môn Tiếng Việt nhiều hơn. Hy vọng bài viết giúp quý phụ huynh tìm ra những tài liệu phù hợp nhất cho con em mình trên hành trình học tập.
Hãy ghé thăm loigiaihay.edu.vn để tìm kiếm thêm nhiều tài liệu hữu ích khác cho con bạn!


 Phiếu Ôn Tập Cuối Tuần Môn Toán Lớp 2
Phiếu Ôn Tập Cuối Tuần Môn Toán Lớp 2 Cuốn Sách Giải Toán Có Lời Văn Lớp 2
Cuốn Sách Giải Toán Có Lời Văn Lớp 2 Sách Chinh Phục Nâng Cao Toán 2
Sách Chinh Phục Nâng Cao Toán 2 Bộ Sách Đề Ôn Luyện Và Tự Kiểm Tra Toán Lớp 2
Bộ Sách Đề Ôn Luyện Và Tự Kiểm Tra Toán Lớp 2

 Bài toán ví dụ tính khoảng cách giữa hai mặt phẳng
Bài toán ví dụ tính khoảng cách giữa hai mặt phẳng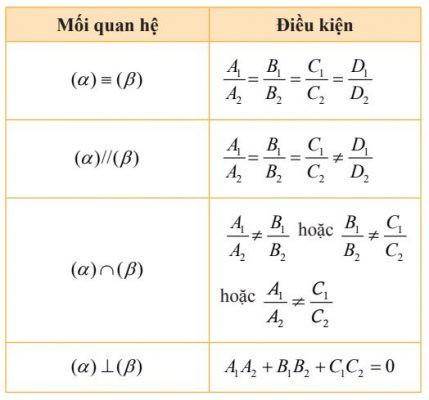 Vị trí tương đối giữa hai mặt phẳng
Vị trí tương đối giữa hai mặt phẳng Bài toán ví dụ về vị trí tương đối của mặt phẳng
Bài toán ví dụ về vị trí tương đối của mặt phẳng Các dạng toán viết phương trình mặt phẳng (1)
Các dạng toán viết phương trình mặt phẳng (1) 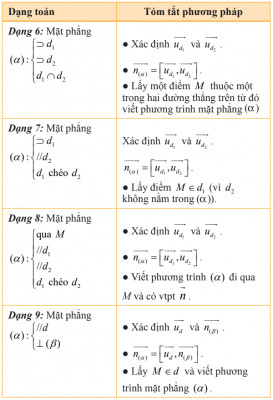 Các dạng toán viết phương trình mặt phẳng (2)
Các dạng toán viết phương trình mặt phẳng (2)  Các dạng toán viết phương trình mặt phẳng (3)
Các dạng toán viết phương trình mặt phẳng (3) Bài tập về phương trình mặt phẳng
Bài tập về phương trình mặt phẳng
 Hình ảnh 2
Hình ảnh 2 Hình ảnh 3
Hình ảnh 3 Hình ảnh 4
Hình ảnh 4 Hình ảnh 5
Hình ảnh 5  Hình ảnh 6
Hình ảnh 6

 Bài tập về đại lượng tỉ lệ thuận lớp 7
Bài tập về đại lượng tỉ lệ thuận lớp 7
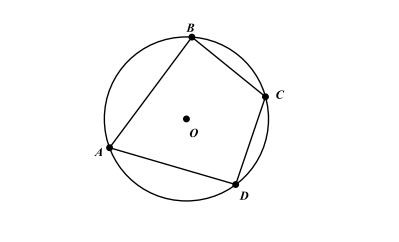 Ví dụ về tứ giác nội tiếp
Ví dụ về tứ giác nội tiếp Hình vẽ minh họa bài 2
Hình vẽ minh họa bài 2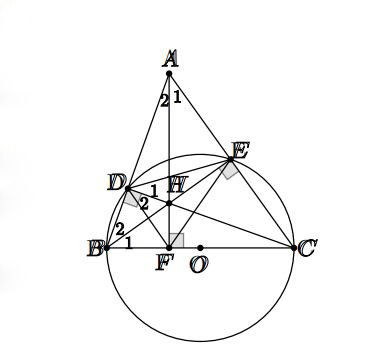 Hình vẽ minh họa bài 3
Hình vẽ minh họa bài 3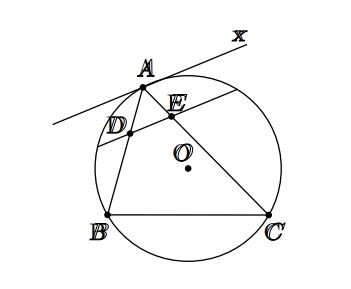 Hình vẽ minh họa bài 4
Hình vẽ minh họa bài 4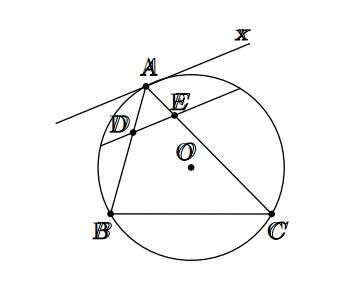 Hình vẽ minh họa bài 5
Hình vẽ minh họa bài 5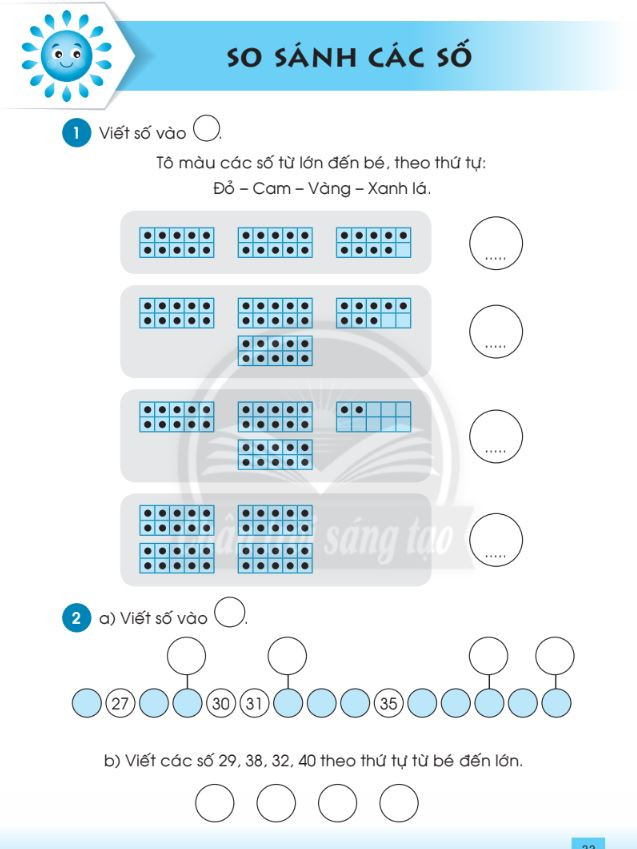
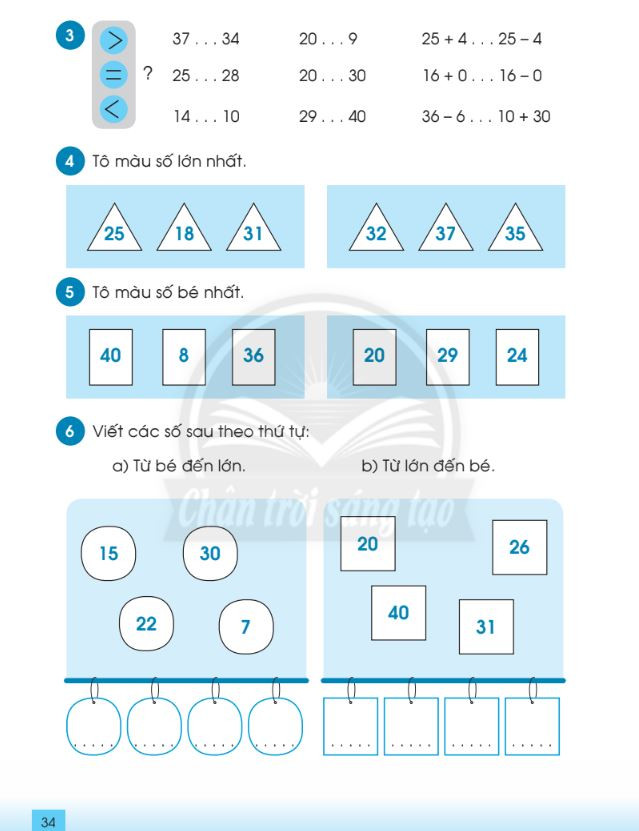 Bài tập so sánh số có hai chữ số – File 2
Bài tập so sánh số có hai chữ số – File 2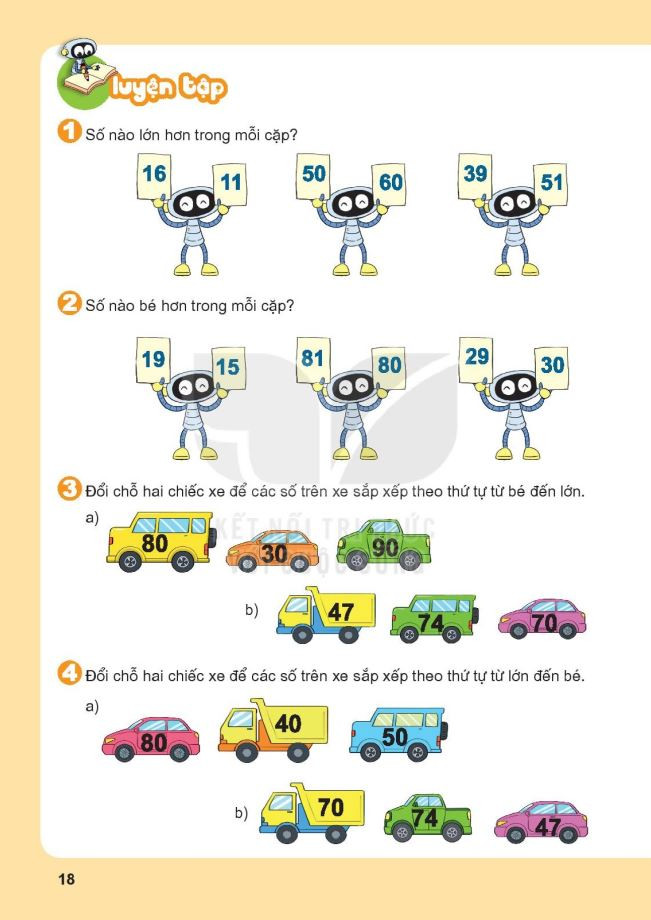 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 1
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 1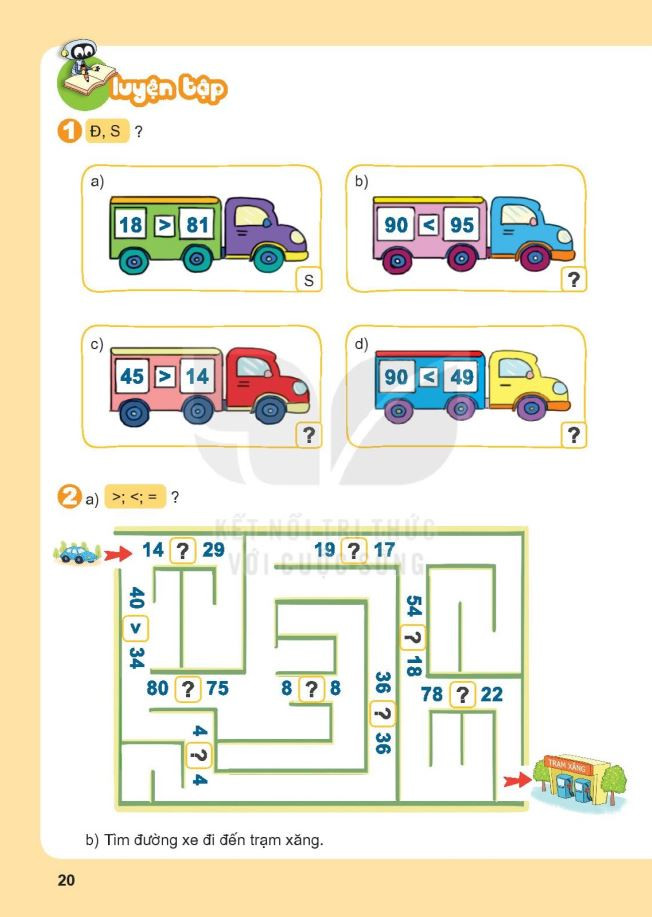 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 2
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 2 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 3
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 3