Trong bài viết này, chúng ta sẽ tìm hiểu về đa thức một biến, những kiến thức cơ bản cũng như các dạng bài tập thường gặp. Đặc biệt, bài viết không chỉ đem lại kiến thức lý thuyết mà còn có các bài tập kèm theo lời giải chi tiết, giúp các em học sinh dễ dàng tiếp cận và hiểu rõ hơn về chủ đề này.
I. Lý thuyết về đa thức một biến lớp 7
1. Đa thức một biến là gì?
Đa thức một biến (hay còn gọi là đơn thức) là biểu thức đại số có dạng tích của một số thực với một lũy thừa của biến, trong đó số thực gọi là hệ số, và số mũ của lũy thừa là bậc của đa thức.
Một số khái niệm cơ bản là:
- Số 0 được coi là một đa thức bậc 0.
- Đa thức bậc 0 không có bậc.
2. Cộng, trừ, nhân đa thức
Để cộng (hay trừ) hai đa thức một biến cùng bậc với nhau, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên lũy thừa của biến. Kết quả thu được là một đa thức một biến.
Để nhân hai đa thức một biến với nhau, ta nhân các hệ số với nhau và nhân các lũy thừa của biến với nhau. Kết quả cũng sẽ là một đa thức một biến.
3. Đa thức một biến là gì?
Đa thức một biến (gọi tắt là đa thức) là tổng các đơn thức của cùng một biến, mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Số 0 là một đa thức và được gọi là đa thức không.
Ta ký hiệu đa thức bằng một chữ cái in hoa, đôi khi ký hiệu thêm biến trong ngoặc đơn.
Lý thuyết về đa thức một biến
4. Khái niệm rút gọn và sắp xếp đa thức một biến
Rút gọn đa thức một biến là thực hiện các phép toán cộng, trừ các đơn thức cùng bậc, được thực hiện bằng cách viết chúng dưới dạng rút gọn và sắp xếp các hạng tử của nó theo lũy thừa giảm dần của biến.
5. Bậc và các hệ số của đa thức một biến
Trong một đa thức rút gọn và khác đa thức không bậc
Bậc của hạng tử có bậc cao nhất chính là bậc của đa thức đó.
Hệ số của hạng tử có bậc cao nhất chính là hệ số cao nhất của đa thức đó.
Hệ số của hạng tử bậc 0 chính là hệ số tự do của đa thức đó.
6. Nghiệm của đa thức một biến
Nếu tại x = a, đa thức F(x) có giá trị bằng 0, tức là F(a) = 0 thì ta gọi a (hay x = a) là một nghiệm của đa thức F(x).
II. Bài tập về đa thức một biến lớp 7
Dạng 1: Nhận biết đa thức một biến, đa thức một biến
+ Phương pháp
Để nhận biết một biểu thức là đa thức một biến, chúng ta cần căn cứ vào định nghĩa của đa thức một biến để phân tích.
+ Các ví dụ
Ví dụ 1
Trong các biểu thức sau, biểu thức nào là đa thức một biến?
a) 2x^4.
b) 2 – (4/5)y^2.
c) 4x^3y^2.
d) x + y + z.
e) (1/2)x.
f) -5x^2.
g) 0.
h) 2.
Hướng dẫn giải
Các biểu thức là đa thức một biến là:
a) 2x^4.
e) (1/2)x.
f) -5x^2.
g) 0.
h) 2.
Ví dụ 2
Trong các đa thức sau, đa thức nào là đa thức một biến?
a) 3x^2 + 4x + 1.
b) 1/x^2 + 2x – 3.
c) (x^2 – 4x)/2022.
d) xy + x + y – 1.
e) √(x^2 + 4x + 9).
f) 4x/(y – 2).
g) x^2022.
h) (3/2)x – xy^2.
Hướng dẫn giải
Các đa thức là đa thức một biến là:
a) 3x^2 + 4x + 1.
c) (x^2 – 4x)/2022.
g) x^2022.
Dạng 2: Rút gọn đa thức một biến, đa thức một biến
+ Phương pháp
Áp dụng quy tắc cộng, trừ, nhân các đa thức một biến.
+ Các ví dụ
Ví dụ 1
Rút gọn các đa thức sau:
a) 2x^3 + 3x^3 – (2/3)x^3.
b) 2/3x^2 – (3/4)x^2 + (-1/2)x^2.
c) 2x^2 – (-2x)^2 + 4x(-1/2)x.
Hướng dẫn giải
a) 2x^3 + 3x^3 – (2/3)x^3 = (2 + 3 – 2/3)x^3 = (13/3)x^3.
b) 2/3x^2 – (3/4)x^2 – (1/2)x^2 = (2/3 – 3/4 – 1/2)x^2 = (-7/12)x^2.
c) 2x^2 – (-2x)^2 + 4x(-1/2)x = 2x^2 – 4x^2 – 2x^2 = -4x^2.
Ví dụ 2
Rút gọn các biểu thức sau (nếu được) rồi sắp xếp thành từng nhóm gồm các đơn thức đồng bậc:
5x^2; 4x^3; (-1/2)x^2; √3x^4; ((1/2)x)^2; (6x)(-9x^3); x(-2x)^2; 4x^2 + 2x^2.
Hướng dẫn giải
Ta có
((1/2)x)^2 = 1/4.x^2; (6x)(-9x^3) = -54x^4; x(-2x)^2 = 4x^3; 4x^2 + 2x^2 = 6x^2.
Suy ra các nhóm đơn thức đồng bậc là:
– Các đơn thức bậc 2 gồm 5x^2; ((1/2)x)^2; 4x^2 + 2x^2.
– Các đơn thức bậc 3 gồm 4x^3; x(-2x)^2.
– Các đơn thức bậc 4 gồm √3x^4; (6x)(-9x^3).
Dạng 3: Xác định bậc, hệ số của đơn thức, đa thức
+ Phương pháp
Bước 1: Rút gọn đơn thức, đa thức. Đối với đa thức, ta cần sắp xếp các hạng tử của đa thức theo lũy thừa giảm dần của biến.
Bước 2: Xác định bậc, hệ số của đơn thức, đa thức.
+ Các ví dụ
Ví dụ 1
Rút gọn rồi xác định bậc, hệ số của các đơn thức sau:
a) ((-2/3)x)^3
b) ((3/2)x^3)((-1/3)x)^2.
c) 3x^2((-2x)^3)((3/2)x^4).
Hướng dẫn giải
a) ((-2/3)x)^3 = (-2/3)^3 * x^3 = (-8/27)x^3.
Đơn thức (-8/27)x^3 có hệ số bằng (-8/27) và bậc 3.
b) ((3/2)x^3)((-1/3)x)^2 = ((3/2)x^3)((-1/3)^2 x^2) = (3/2) (1/9) * x^5 = (1/6)x^5.
Đơn thức (1/6)x^5 có hệ số bằng (1/6) và bậc 5.
c) 3x^2 (-2x)^3 ((3/2)x^4) = 3 (-2)^3 ((3/2)) (x^2 x^3 x^4) = 3 (-8) (3/2) x^9 = -36x^9.
Đơn thức -36x^9 có hệ số bằng -36 và bậc 9.
Ví dụ 2
Viết đa thức thỏa mãn điều kiện sau:
a) Có hệ số bằng (-2/3) và bậc bằng 4.
b) Có hệ số bằng hệ số của đa thức 2x^3 và cùng bậc với đa thức ((1/2)x^2)^4.
Hướng dẫn giải
a) Đơn thức cần tìm là (-2/3)x^4.
b) Đơn thức có hệ số bằng 2 và cùng bậc là 2x^4.
Ví dụ 3
Xác định bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức sau:
a) M(x) = x^4 + 2x^3 – 3x^2 + 6x – 1.
b) N(x) = 6x^2 – 3x^3 + 9x^4 – 3x + 2.
c) P(x) = 2x^2 + 3x^4 – x + 4 – 3x^3 + 2x^2 – 4x^3 – 2x^2.
Hướng dẫn giải
a) Đa thức M(x) có bậc 4, hệ số cao nhất bằng 1 và hệ số tự do bằng -1.
b) Ta có N(x) = 9x^4 – 3x^3 + 6x^2 – 3x + 2.
Đa thức N(x) có bậc 4, hệ số cao nhất bằng 9 và hệ số tự do bằng 2.
c) Ta có P(x) = 3x^4 + (-3x^3 – 4x^3) + (2x^2 + 2x^2 – 2x^2) – x + 4 = 3x^4 – 7x^3 + 2x^2 – x + 4.
Đa thức P(x) có bậc 4, hệ số cao nhất bằng 3 và hệ số tự do bằng 4.
Dạng 4: Tính giá trị của đơn thức, đa thức
+ Phương pháp
Bước 1: Rút gọn đơn thức, đa thức.
Bước 2: Thay giá trị của biến vào đơn thức, đa thức và thực hiện các phép tính.
+ Các ví dụ
Ví dụ 1
Tính giá trị của các đa thức sau tại x = -2; x = 1.
a) A = (1/4)x^3.
b) B = ((1/4)x^3)((-3/2)x^2)^2((1/2)x)^4.
Hướng dẫn giải
a) Thay x = -2 vào đa thức A, ta có A = (1/4)(-2)^3 = (1/4)(-8) = -2.
Thay x = 1 vào đa thức A, ta có A = (1/4)(1)^3 = (1/4)(1) = (1/4).
Vậy A = -2 khi x = -2 và A = 1/4 khi x = 1.
b) B = ((1/4)x^3)((-3/2)x^2)^2((1/2)x)^4 = [1/4 (-3/2)^2 (1/2)^4].[x^3 (x^2)^2(x)^4] = (9/64)x^9.
Thay x = -2 vào đa thức B, ta có B = (9/64)(-2)^9 = (9/64)(-512) = -72.
Thay x = 1 vào đa thức B, ta có B = (9/64)(1)^9 = (9/64)(1) = (9/64).
Vậy B = -72 khi x = -2 và B = 9/64 khi x = 1.
Ví dụ 2
Cho đơn thức A = (1/2)a^2 x^4 với a là hàng số. Tìm giá trị của a để đơn thức có giá trị bằng 2 khi x = 2.
Hướng dẫn giải
Vì đơn thức có giá trị bằng 2 khi x = 2 nên (1/2)a^2 * 2^4 = 2 sẽ cho ta (1/2)a^2 * 16 = 2 → (1/2)a^2 * 16 = 2 → a^2 = 1/8 → a = -1/2 hoặc a = 1/2.
Vậy a = -1/2 hoặc a = 1/2 thì đơn thức có giá trị bằng 2 khi x = 2.
Ví dụ 3
Cho đa thức P(x) = x^4 + x^2 + 1. Tính P(-2); P(0); P(1).
Hướng dẫn giải
P(-2) = (-2)^4 + (-2)^2 + 1 = 16 + 4 + 1 = 21.
P(0) = (0)^4 + (0)^2 + 1 = 0 + 0 + 1 = 1.
P(1) = (1)^4 + (1)^2 + 1 = 1 + 1 + 1 = 3.
Dạng 5: Chứng minh giá trị của đa thức không phụ thuộc vào giá trị của biến
+ Phương pháp
Để chứng minh giá trị của đa thức không phụ thuộc vào giá trị của biến, ta chứng minh đa thức là một số không đổi (hằng số).
+ Ví dụ
Ví dụ 1
Chứng minh rằng giá trị của đa thức sau không phụ thuộc vào giá trị của biến.
a) A(x) = 4x^3 + 3x^2 – 4x – 1 + 2x – x^3 – 3x^2 – 3x^3 + 2x + 4.
b) B(x) = 2x^3 – x^5 + 4x^2 – 3 + 2x – 2x^3 + x^5 + 3 – 2x – 4x^2.
c) C(x) = x^2(x^3 + 2x) – x(x^4 + 1) – 2x^3 + x – 2.
Hướng dẫn giải
a) A(x) = 4x^3 + 3x^2 – 4x – 1 + 2x – x^3 – 3x^2 – 3x^3 + 2x + 4
= (4x^3 – x^3 – 3x^3) + (3x^2 – 3x^2) + (-4x + 2x + 2x) + (-1 + 4)
= 0.x^3 + 0.x^2 + 0.x + 3 = 3.
3 là hằng số nên giá trị của đa thức A(x) không phụ thuộc vào giá trị của biến.
b) B(x) = 2x^3 – x^5 + 4x^2 – 3 + 2x – 2x^3 + x^5 + 3 – 2x – 4x^2
= (-x^5 + x^5) + (2x^3 – 2x^3) + (4x^2 – 4x^2) + (2x – 2x) + (-3 + 3)
= 0.x^5 + 0.x^3 + 0.x^2 + 0.x + 0 = 0.
0 là hằng số nên giá trị của đa thức B(x) không phụ thuộc vào giá trị của biến.
c) C(x) = x^2(x^3 + 2x) – x(x^4 + 1) – 2x^3 + x – 2
= x^5 + 2x^3 – x^5 – x – 2x^3 + x – 2
= (x^5 – x^5) + (2x^3 – 2x^3) + (x – x) – 2
= 0.x^5 + 0.x^3 + 0.x – 2 = -2
-2 là hằng số nên giá trị của đa thức C(x) không phụ thuộc vào giá trị của biến.
Ví dụ 2
Cho đa thức M(x)=4r’-3x+6mr-r-3-3r’. Tìm giá trị của m để đa thức M(x) không phụ thuộc vào giá trị của biến.
Kết luận
Thông qua bài viết “Bài tập về đa thức một biến lớp 7 có đáp án cực chi tiết”, chúng ta đã cùng nhau đi qua các kiến thức cơ bản và một số dạng toán thường gặp về đa thức một biến. Học sinh lớp 7 có thể sử dụng bài viết này như một công cụ học tập hiệu quả, giúp các em củng cố và mở rộng kiến thức toán học, đặc biệt là trong phần đại số.
Hy vọng rằng, những kiến thức và phương pháp được trình bày trong bài viết sẽ hỗ trợ các em trong hành trình học tập và đạt được thành tích cao trong các bài kiểm tra sắp tới. Chúc các em luôn học tập hiệu quả và tìm thấy niềm vui trong mỗi bài toán!
Link tài liệu tham khảo: Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 7 tập 2
TKbooks tự hào là nhà xuất bản sách tham khảo lớp 7 hàng đầu tại Việt Nam.
TKbooks.vn
Xác định đúng năng lực hiện tại của trẻ
Tư duy toán học với các phép tính dành cho trẻ
Phương pháp học tập thú vị, sáng tạo và kích thích sự ham học hỏi
Hình lập phương
Hình tam giác
Hình tròn
Sách Chinh phục nâng cao Toán 3
Cuốn sách Để giỏi Toán con phải giỏi tính 3
Bộ sách Vở Bài tập nâng cao Toán 3
Cuốn sách Phiếu bài tập cuối tuần Toán 3
Bài 5 – Phần trắc nghiệm – Phép trừ số có hai chữ số cho số có hai chữ số
Hình ảnh bài tập tự luận 1
Hình ảnh bài tập khó
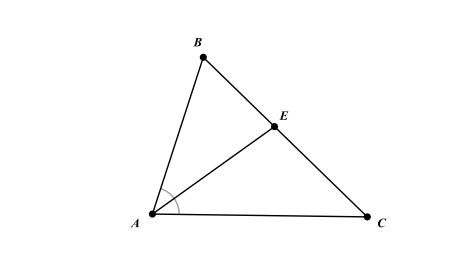Đường phân giác của tam giác
Bài tập Unit 1 – File 1
File 2
File 3
File 4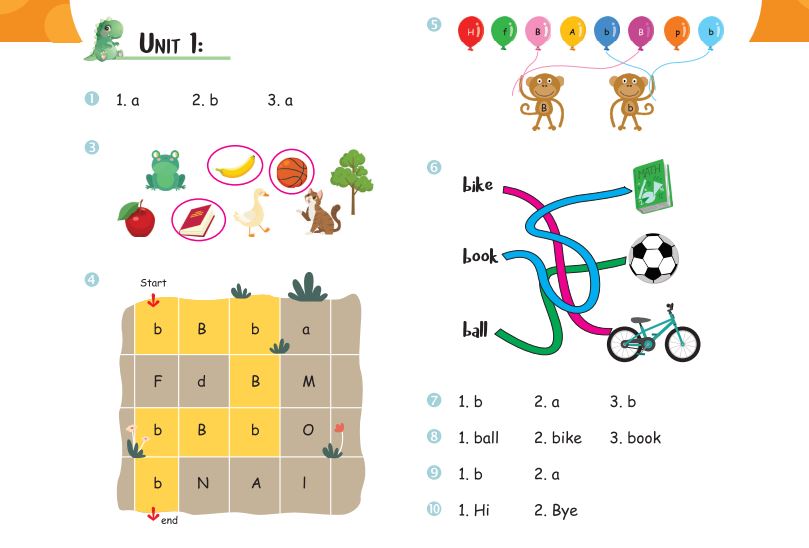 
Đáp án bài tập tiếng Anh Unit 1
Bài đọc trong đề thi giữa kì số 2
Bài đọc trong đề thi giữa kì số 3 