Vecto là một khái niệm quan trọng trong chương trình Toán học THPT. Kiến thức này chiếm khoảng 10% trong các bài toán thi THPT Quốc Gia, chính vì vậy, các em cần nắm vững để có được điểm số cao. Trong bài viết này, chúng ta sẽ tìm hiểu sâu về vecto, các phép toán với vecto, cũng như ứng dụng của chúng trong giải toán.
I. Khái Niệm Vecto
1. Khái niệm Vecto
Vecto là một đoạn thẳng có hướng.
Vecto được biểu diễn từ điểm đầu A đến điểm cuối B, ký hiệu là ( vec{AB} ).
Hình ảnh minh họa cho vecto  Hình ảnh minh họa cho vecto
Hình ảnh minh họa cho vecto
2. Vecto cùng phương, vecto cùng hướng
Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Theo định nghĩa trên, ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vecto ( vec{AB} ) và ( vec{AC} ) cùng phương.
3. Hai vecto bằng nhau
Mỗi vecto có một độ dài, đó chính là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto được ký hiệu là ( |vec{AB}| ), và ( |AB| = AB ).
Hai vecto ( vec{a} ) và ( vec{b} ) được gọi là bằng nhau nếu chúng cùng phương, cùng chiều và có cùng độ dài, ký hiệu ( vec{a} = vec{b} ).
4. Vecto – không
Vecto này được ký hiệu là ( vec{AA} ) có điểm đầu và điểm cuối trùng nhau được gọi là vecto không.
II. Tổng Và Hiệu Của Hai Vecto
1. Tổng của hai vecto
Hai vecto ( vec{a} ) và ( vec{b} ) được cộng lại khi có một điểm A tùy ý, vậy ( vec{AB} = vec{a} ) và ( vec{BC} = vec{b} ).
Vecto ( vec{AC} ) được gọi là tổng của hai vecto ( vec{a} ) và ( vec{b} ). Ta ký hiệu tổng này là:
[ vec{AC} = vec{a} + vec{b} ]
2. Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì ( vec{AB} + vec{AD} = vec{AC} ).
3. Tính chất của phép cộng các vecto
Với ba vecto tùy ý, ta có:
-
( vec{a} + vec{b} = vec{b} + vec{a} ) (tính chất giao hoán);*
-
( (vec{a} + vec{b}) + vec{c} = vec{a} + (vec{b} + vec{c}) ) (tính chất kết hợp);*
-
( vec{a} + vec{0} = vec{0} + vec{a} = vec{a} ) (tính chất của vecto – không).*
4. Hiệu của hai vecto
a) Vecto đối
Cho vecto ( vec{a} ). Vecto có cùng độ dài và ngược hướng với ( vec{a} ) được gọi là vecto đối của vecto ( vec{a} ), ký hiệu là ( -vec{a} ).
Mỗi vecto đều có vecto đối, chình vì vậy vecto đối của ( vec{AB} ) là ( vec{BA} ).
b) Định nghĩa hiệu của hai vecto
Định nghĩa: Cho hai vecto ( vec{a} ) và ( vec{b} ). Ta gọi hiệu của hai vecto ( vec{a} ) và ( vec{b} ) là vecto ( vec{a} + -(vec{b}) ), ký hiệu là ( vec{a} – vec{b} ).
Như vậy,
[ vec{a} – vec{b} = vec{a} + (-vec{b}) ]
5. Ứng dụng
a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi ( vec{IA} + vec{IB} = vec{0} ).
b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi ( vec{GA} + vec{GB} + vec{GC} = vec{0} ).
Hình minh họa cho ứng dụng của hiệu hai vecto 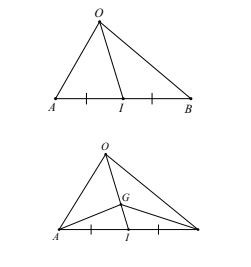 Hình minh họa cho ứng dụng của hiệu hai vecto
Hình minh họa cho ứng dụng của hiệu hai vecto
III. Tích Của Vecto Với Một Số
1. Định nghĩa
Cho số k khác 0 và vecto ( vec{a} neq 0 ).
Tích của vecto ( vec{a} ) với số k là một vecto, ký hiệu là ( k.vec{a} ).
- Nếu ( k > 0 ): thì ( k.vec{a} ) cùng hướng với ( vec{a} ).
- Nếu ( k < 0 ): thì ( k.vec{a} ) ngược hướng với ( vec{a} ).
- Độ dài ( |k.vec{a}| = |k| . |vec{a}| )
Bài tập ví dụ về tích của vecto  Bài tập ví dụ về tích của vecto
Bài tập ví dụ về tích của vecto
2. Tính chất
Với hai vecto ( vec{a} ) và ( vec{b} ) bất kỳ, với mỗi số h và k, ta có:
- ( vec{a} . vec{b} = vec{b} . vec{a} )
- ( k(vec{a} + vec{b}) = k.vec{a} + k.vec{b} )
- ( (h + k).vec{a} = h.vec{a} + k.vec{a} )
- ( 1.vec{a} = vec{a}; (-1).vec{a} = -(vec{a}) )
- ( (vec{a} pm vec{b})^2 = vec{a}^2 pm 2.vec{a}.vec{b} + vec{b}^2 )
- ( vec{a}^2 – vec{b}^2 = (vec{a} – vec{b})(vec{a} + vec{b}) )
3. Trung Điểm Của Đoạn Thẳng Và Trọng Tâm Của Tam Giác
a) Nếu ( I ) là trung điểm của đoạn thẳng ( AB ) thì với mỗi điểm ( M ), ta có:
[ vec{MA} + vec{MB} = 2.vec{MI} ]
b) Nếu ( G ) là trọng tâm của tam giác ( ABC ) thì với mỗi điểm ( M ), ta có:
[ vec{GA} + vec{GB} + vec{GC} = 3.vec{MG} ]
4. Điều kiện để hai vecto cùng phương
Điều kiện cần và đủ để hai vecto ( vec{a} ) và ( vec{b} ) ( ( vec{b} neq 0 )) cùng phương là có một số k để:
[ vec{a} = k.vec{b} ]
5. Phân tích một vecto theo hai vecto không cùng phương
Cho hai vecto ( vec{a} ) và ( vec{b} ) không cùng phương. Khi đó mỗi vecto ( vec{x} ) đều phân tích được một cách duy nhất theo hai vecto ( vec{a} ) và ( vec{b} ), nghĩa là có duy nhất cặp số h, k sao cho:
[ vec{x} = h.vec{a} + k.vec{b} ]
IV. Hệ Trục Tọa Độ
1. Trục và độ dài đoạn thẳng trên trục
a) Trục tọa độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm 0 gọi là điểm gốc và một vecto đơn vị ( vec{e} ).
Ta ký hiệu trục đó là (0; ( vec{e} )).
b) Cho M là một điểm tùy ý trên trục. Khi đó có duy nhất một số k sao cho ( vec{OM} = k.vec{e} ). Ta gọi số k đó là tọa độ của điểm M đối với trục đã cho.
2. Hệ trục tọa độ
a) Định nghĩa
Hệ trục tọa độ (O; ( vec{i}, vec{j} )) gồm hai trục (O; ( vec{i} )) và (O; ( vec{j} )) vuông góc với nhau. Điểm gốc 0 chung của hai trục gọi là gốc tọa độ. Trục (O; ( vec{i} )) được gọi là trục hoành và ký hiệu là Ox, trục (O; ( vec{j} )) được gọi là trục tung và ký hiệu là Oy. Các vecto ( vec{i} ) và ( vec{j} ) là các vecto đơn vị trên Ox và Oy với ( |vec{i}| = |vec{j}| = 1 ). Hệ trục tọa độ này còn được ký hiệu là Oxy.
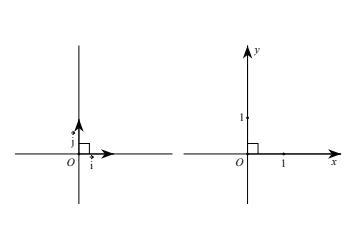 Mặt phẳng tọa độ Oxy
Mặt phẳng tọa độ Oxy
b) Tọa độ của vecto
Trong mặt phẳng Oxy cho một vecto ( vec{u} ) tùy ý. Vẽ và gọi A1, A2 lần lượt là hình chiếu vuông góc của A lên Ox và Oy.
Ta có:
[ vec{OA} = vec{OA1} + vec{OA2} ]
và cặp số duy nhất (x;y) để ( vec{OA1} = x.vec{i}, vec{OA2} = y.vec{j} ).
Như vậy, ( vec{u} = x.vec{i} + y.vec{j} ).
Cặp số (x;y) duy nhất đó được gọi là tọa độ của vecto ( vec{u} ) đối với hệ tọa độ Oxy và viết ( vec{u} = (x;y) ) hoặc ( vec{u}(x;y) ).
Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độ của vecto ( vec{u} ).
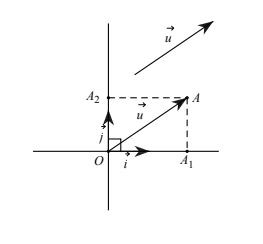 Cách xác định tọa độ của vecto
Cách xác định tọa độ của vecto
c) Tọa độ của hai điểm
Trong mặt phẳng cho hai điểm A(xA;yA) và B(xB;YB).
Ta có: ( vec{AB} = (xB – xA; yB – yA) )
3. Tọa độ của các vecto ( vec{u} + vec{v}; vec{u} – vec{v}; k.vec{u} )
Ta có các công thức sau:
Cho ( vec{u} = (u_1;u_2), vec{v} = (v_1;v_2) ).
Khi đó:
- ( vec{u} + vec{v} = (u_1 + u_2; v_1 + v_2) )
- ( vec{u} – vec{v} = (u_1 – u_2; v_1 – v_2) )
- ( k.vec{u} = (ku_1; ku_2), k in R )
Nhận xét rằng, hai vecto ( vec{u} = (u_1;u_2), vec{v} = (v1;v2) ) với ( v neq 0 ) cùng phương khi và chỉ khi:
Phép tính diện tích tam giác ABC với ( vec{AB} = (a_1;b_1); AC=(a_2,b_2) )
4. Một số điều kiện xác định điểm khác
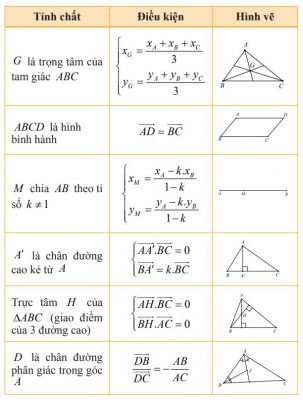 Một số điều kiện xác định điểm khác
Một số điều kiện xác định điểm khác
V. Bài Tập Luyện Tập
Dưới đây là một số dạng toán cơ bản về vecto để các em luyện tập và ôn luyện kiến thức:
 Bài tập ví dụ về vecto
Bài tập ví dụ về vecto
 Bài tập ví dụ về vecto (tiếp theo)
Bài tập ví dụ về vecto (tiếp theo)
Các dạng toán khác về vecto được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.
Tkbooks.vn
 Đáp án đề thi vào lớp 10 tỉnh Quảng Bình môn Tiếng Anh năm học 2024 – 2025
Đáp án đề thi vào lớp 10 tỉnh Quảng Bình môn Tiếng Anh năm học 2024 – 2025
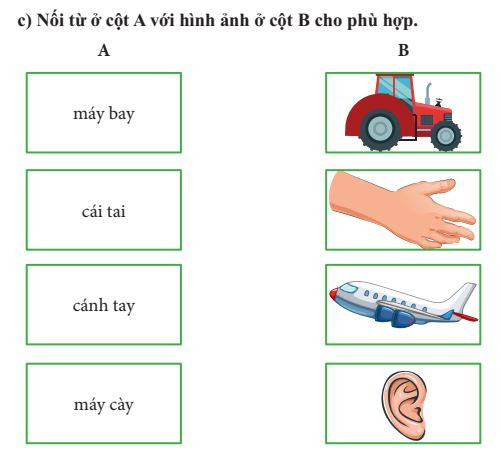
 Bài tập đặt câu số 4
Bài tập đặt câu số 4
 Trường THPT dân lập Lê Văn Thiêm
Trường THPT dân lập Lê Văn Thiêm Trường THPT dân lập Đinh Tiên Hoàng Cơ sở 3
Trường THPT dân lập Đinh Tiên Hoàng Cơ sở 3 Trường THPT dân lập Văn Xuân
Trường THPT dân lập Văn Xuân Trường Phổ thông Liên cấp Bảo Long
Trường Phổ thông Liên cấp Bảo Long Trường THCS & THPT dân lập Hồng Hà
Trường THCS & THPT dân lập Hồng Hà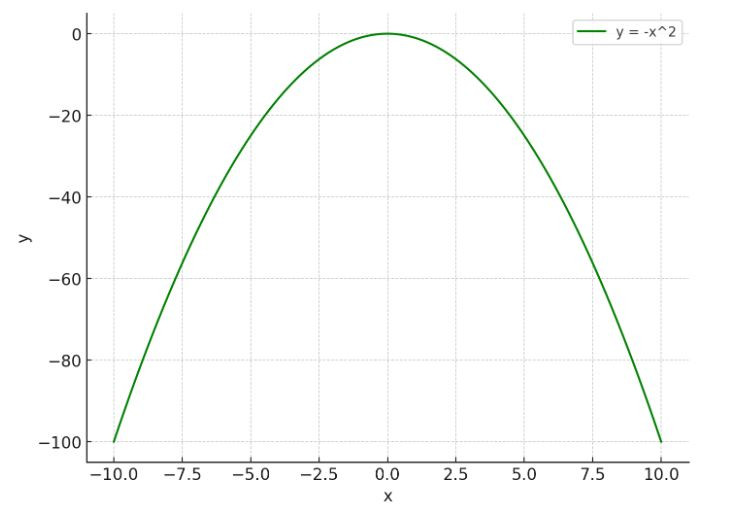
 Bài tập thực hành thêm về hàm số bậc 2 lớp 9
Bài tập thực hành thêm về hàm số bậc 2 lớp 9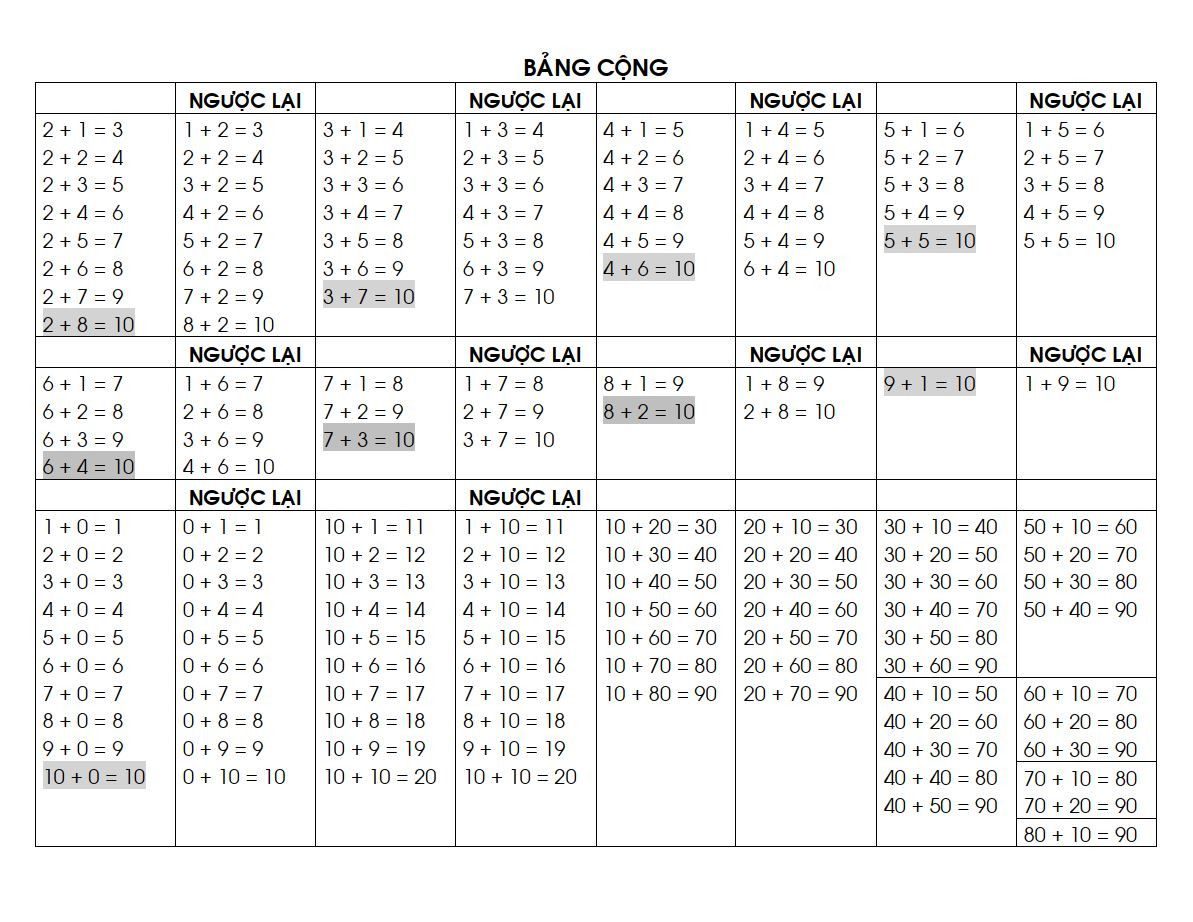

 Hình minh họa cho ứng dụng của hiệu hai vecto
Hình minh họa cho ứng dụng của hiệu hai vecto Bài tập ví dụ về tích của vecto
Bài tập ví dụ về tích của vecto Mặt phẳng tọa độ Oxy
Mặt phẳng tọa độ Oxy Cách xác định tọa độ của vecto
Cách xác định tọa độ của vecto Một số điều kiện xác định điểm khác
Một số điều kiện xác định điểm khác Bài tập ví dụ về vecto
Bài tập ví dụ về vecto Bài tập ví dụ về vecto (tiếp theo)
Bài tập ví dụ về vecto (tiếp theo)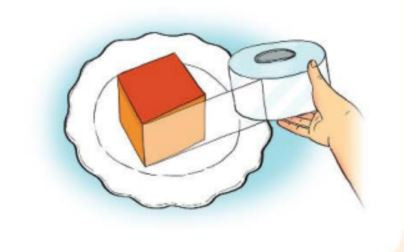
 Hình ảnh minh họa bài 4 – Phần Luyện tập
Hình ảnh minh họa bài 4 – Phần Luyện tập
 Bộ sách Đề kiểm tra Tiếng Việt 3
Bộ sách Đề kiểm tra Tiếng Việt 3  Bộ sách Bài tập hàng ngày Tiếng Việt lớp 3
Bộ sách Bài tập hàng ngày Tiếng Việt lớp 3  Cuốn sách Hướng dẫn cách viết Tập làm văn 3
Cuốn sách Hướng dẫn cách viết Tập làm văn 3  Cuốn sách Chinh phục nâng cao Tiếng Việt lớp 3
Cuốn sách Chinh phục nâng cao Tiếng Việt lớp 3 
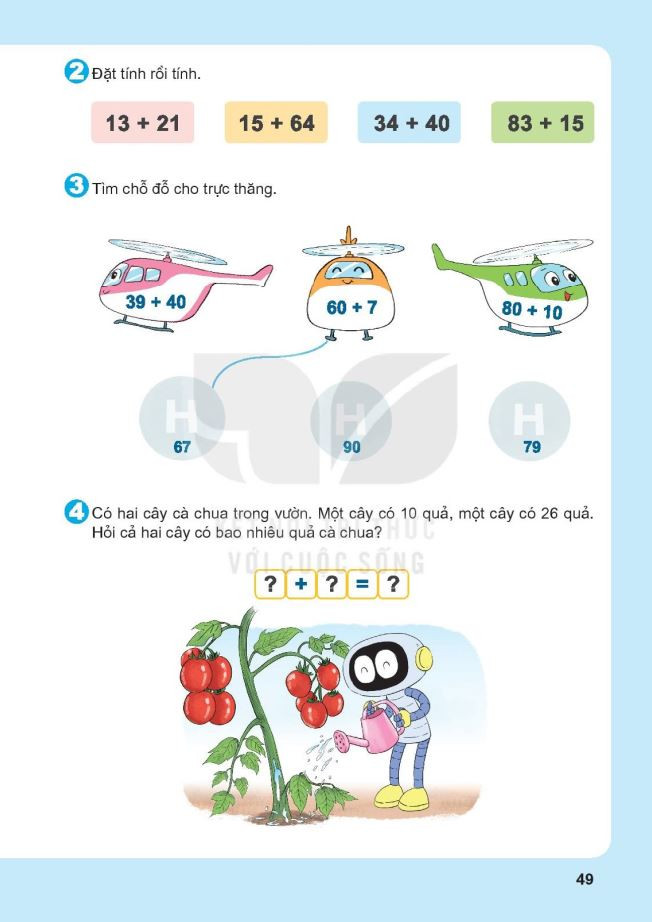 Bài tập phép cộng số có hai chữ số với số có hai chữ số
Bài tập phép cộng số có hai chữ số với số có hai chữ số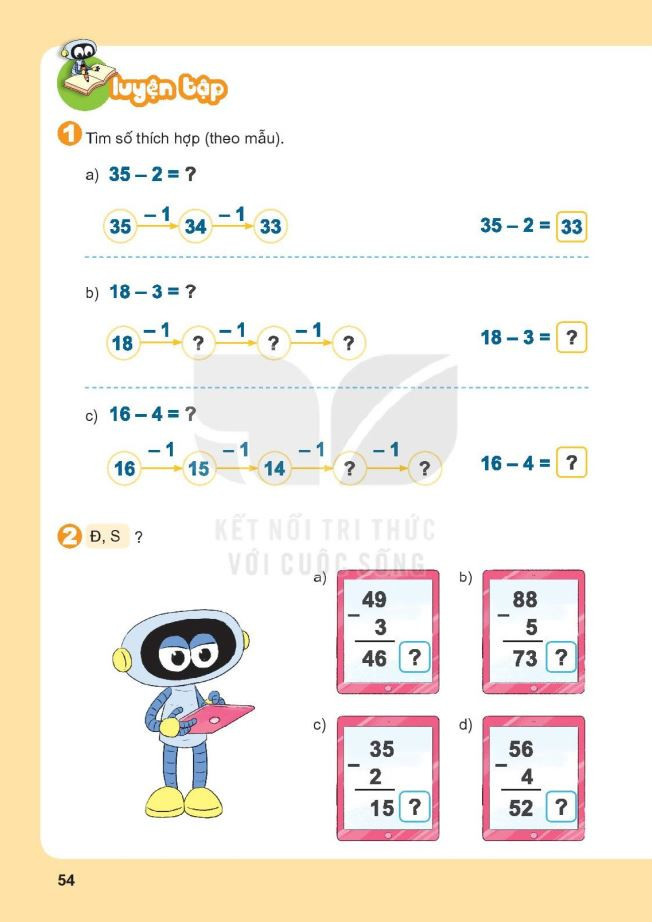 Bài tập phép trừ số có hai chữ số cho số có một chữ số
Bài tập phép trừ số có hai chữ số cho số có một chữ số