Bài tập góc nhọn, góc tù, góc bệt và góc vuông là những kiến thức cơ bản và quan trọng trong chương trình Toán lớp 4. Bộ tài liệu dưới đây cung cấp cho các em học sinh các dạng bài tập trắc nghiệm và tự luận để ôn tập và hiểu sâu hơn về các loại góc.
Mong rằng các thầy cô và phụ huynh sẽ tìm thấy tài liệu này hữu ích cho việc dạy và học!
I. Bài tập trắc nghiệm
Bài 1: Góc nhọn là góc có số đo?
A. Bằng 180°
B. Lớn hơn 90°
C. Bằng 90°
D. Nhỏ hơn 90°
Bài 2: Góc có số đo bằng 180° là góc?
A. Góc vuông
B. Góc nhọn
C. Góc tù
D. Góc bệt
Bài 3: Góc có số đo góc bằng 90° được gọi là góc gì?
A. Góc vuông
B. Góc nhọn
C. Góc tù
D. Góc bệt
Bài 4:
Một góc có số đo góc là 166°. Nếu chia góc này ra thành hai góc, thì hai góc mới đó có thể là?
A. Một góc vuông, một góc nhọn
B. Một góc vuông, một góc tù
C. Hai góc vuông
D. Hai góc tù
Bài 5:
Cho các số đo góc 90°; 180°; 60°; 91°. Được tên lần lượt các góc?
A. Góc vuông, góc bệt, góc 60° và góc tù
B. Góc vuông, góc bệt, góc nhọn và góc cận
C. Góc vuông, góc bệt, góc nhọn và góc tù
D. Góc 90°, góc bệt, góc nhọn và góc tù
Bài 6:
Tổng số đo của một góc vuông và góc nhọn thì chỉ có thể là:
A. Góc tù
B. Góc bệt
C. Góc vuông
D. Góc nhọn
Bài 7:
Một hình tam giác có 1 góc vuông, vậy hai góc còn lại…?
A. Là 1 góc nhọn, một góc tù
B. Là hai góc vuông
C. Là một góc nhọn, một góc vuông
D. Chỉ có thể là hai góc nhọn
Bài 8:
Một góc tù có số đo là 170°, nếu vẽ một đường thẳng đi qua góc tù và chia góc tù thành hai góc. Vậy thì hai góc mới tạo ra có thể là?
A. Một góc tù, một góc vuông
B. Một góc vuông, một góc tù
C. Một góc vuông, một góc nhọn
D. Hai góc tù
Bài 9: Cho hình vẽ sau:
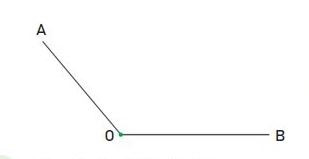 Hình minh họa bài số 9 – Bài tập trắc nghiệmGóc định O là góc gì?
Hình minh họa bài số 9 – Bài tập trắc nghiệmGóc định O là góc gì?
A. Góc bệt
B. Góc nhọn
C. Góc tù
D. Góc bệt
Bài 10: Góc ở hình vẽ dưới đây là góc gì?
 Hình minh họa bài số 9 – Bài tập trắc nghiệmA. Góc nhọn định O cạnh OA, OB
Hình minh họa bài số 9 – Bài tập trắc nghiệmA. Góc nhọn định O cạnh OA, OB
B. Góc vuông định O cạnh OA, OB
C. Góc tù định O cạnh OA, OB
D. Góc bệt định O cạnh OA, OB
Bài 11: Cho hình vẽ dưới đây:
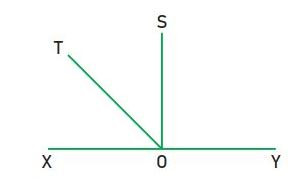 Hình minh họa bài số 11 – Bài tập trắc nghiệmTrong hình vẽ trên có:
Hình minh họa bài số 11 – Bài tập trắc nghiệmTrong hình vẽ trên có:
A. 1 góc tù, 1 góc nhọn, 1 góc vuông
B. 1 góc vuông, 2 góc nhọn
C. 1 góc vuông, 2 góc tù
D. 1 góc tù, 2 góc nhọn
Bài 12: Hình bên dưới có:
 Hình minh họa bài số 11 – Bài tập trắc nghiệmA. 2 góc nhọn, 1 góc vuông, 1 góc tù
Hình minh họa bài số 11 – Bài tập trắc nghiệmA. 2 góc nhọn, 1 góc vuông, 1 góc tù
B. 2 góc nhọn, 2 góc vuông, 2 góc tù
C. 2 góc nhọn, 2 góc vuông, 1 góc tù
D. 1 góc nhọn, 2 góc vuông
Bài 13:
Những phát biểu nào dưới đây em cho là đúng.
A. Góc bệt nhỏ hơn góc tù
B. Góc tù lớn hơn góc vuông
C. Góc nhọn lớn hơn góc bệt
D. Góc nhọn lớn hơn góc vuông
Bài 14: Câu nào sau đây đúng:
A. Hình tứ giác có 4 góc vuông
B. Hình chữ nhật có 4 góc nhọn
C. Hình vuông có 4 góc bệt
D. Hình chữ nhật có 4 góc vuông
Bài 15:
Tam giác MNP trong hình dưới đây có bao nhiêu góc nhọn?
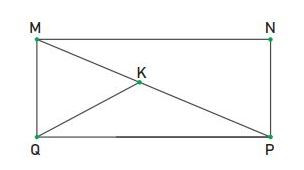 Hình minh họa bài số 15 – Bài tập trắc nghiệmA. 5 góc nhọn
Hình minh họa bài số 15 – Bài tập trắc nghiệmA. 5 góc nhọn
B. 4 góc nhọn
C. 2 góc nhọn
D. 3 góc nhọn
Bài 16: Hình dưới đây có mấy góc nhọn?
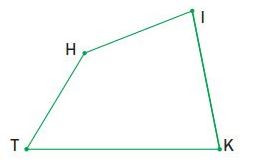 Hình minh họa bài số 16 – Bài tập trắc nghiệmA. 3 góc nhọn
Hình minh họa bài số 16 – Bài tập trắc nghiệmA. 3 góc nhọn
B. 1 góc nhọn
C. 4 góc nhọn
D. 2 góc nhọn
Bài 17: Điền dấu ✔ vào ô trống dưới các góc tù:
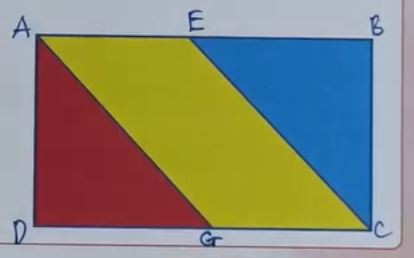 Hình minh họa bài số 17 – Bài tập trắc nghiệm
Hình minh họa bài số 17 – Bài tập trắc nghiệm
Bài 18:
Góc tạo bởi kim giờ và kim phút khi đồng hồ chỉ 15 giờ có số đo là:
A. 60°
B. 90°
C. 120°
D. 180°
Bài 19:
Khi đồng hồ chỉ mấy giờ thì góc tạo bởi hai kim đồng hồ có số đo bằng 180°?
A. 4 giờ
B. 21 giờ
C. 18 giờ
D. 13 giờ
II. Bài tập tự luận
Bài 1: Cho hình ảnh sau:
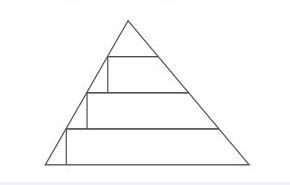 Hình ảnh minh họa bài 1 – Bài tập tự luậna. Hình trên có ….. góc nhọn
Hình ảnh minh họa bài 1 – Bài tập tự luậna. Hình trên có ….. góc nhọn
b. Hình trên có ….. góc vuông
Bài 2:
Cho hình dưới đây, hãy xác định xem B có bao nhiêu góc nhọn? Bao nhiêu góc tù? Bao nhiêu góc vuông? Bao nhiêu góc bệt? Hãy nêu cụ thể tên góc và các cạnh tương ứng.
 Hình minh họa bài số 15 – Bài tập trắc nghiệmBài làm
Hình minh họa bài số 15 – Bài tập trắc nghiệmBài làm
……………………………………………………………………………..
Bài 3:
Cho hình dưới đây, hãy nêu tên các tam giác có:
 Hình minh họa bài số 15 – Bài tập trắc nghiệma. 1 góc vuông
Hình minh họa bài số 15 – Bài tập trắc nghiệma. 1 góc vuông
b. 3 góc nhọn
c. 1 góc tù
Bài làm
……………………………………………………………………………..
Bài 4: Điền vào chỗ chấm:
Cho hình tứ giác ABCD:
 Hình minh họa bài số 17 – Bài tập trắc nghiệma. Cặp cạnh song song là: ……………………………………………………………………………..
Hình minh họa bài số 17 – Bài tập trắc nghiệma. Cặp cạnh song song là: ……………………………………………………………………………..
b. Các cặp cạnh vuông góc là: ……………………………………………………………………………..
c. Góc tù là góc: ……………………………………………………………………………………..
d. Góc nhọn là góc: …………………………………………………………………………………….
Bài 5: Hình vẽ bên có:
 Hình minh họa bài số 17 – Bài tập trắc nghiệm…….. góc nhọn
Hình minh họa bài số 17 – Bài tập trắc nghiệm…….. góc nhọn
…….. góc bệt
…….. góc vuông
…….. góc tù
Hy vọng bộ bài tập góc nhọn, góc tù, góc bệt, góc vuông lớp 4 PDF trên đây đã giúp các em củng cố kiến thức và rèn luyện kỹ năng làm các bài tập liên quan một cách hiệu quả.
Các bài tập trên đều có sẵn trong cuốn Bài tập bổ trợ nâng cao Toán lớp 4 và 50 đề tăng điểm nhanh Tiếng Anh lớp 4. Các em hãy mua ngay hai cuốn sách này để học tốt môn Toán hơn nhé!
Link đọc thử sách Bài tập bổ trợ nâng cao Toán lớp 4: https://drive.google.com/file/d/196iDHopU1z89arXXqkQBU4QkSII1X92m/view
Link đọc thử sách 50 đề tăng điểm nhanh Toán lớp 4: https://drive.google.com/file/d/1GxTFdbwB-LbWNLrpRrlbMj2EMr1U9-X4/view
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 4 hàng đầu tại Việt Nam!
Tkbooks.vn
 File bài tập số 1
File bài tập số 1 File bài tập số 2
File bài tập số 2 File bài tập số 3
File bài tập số 3 File bài tập số 4
File bài tập số 4 File bài tập số 5
File bài tập số 5 File bài tập số 6
File bài tập số 6 File bài tập số 7
File bài tập số 7
 Bài tập chép mẫu
Bài tập chép mẫu Dạng bài tập quan sát và viết mô tả bức tranh
Dạng bài tập quan sát và viết mô tả bức tranh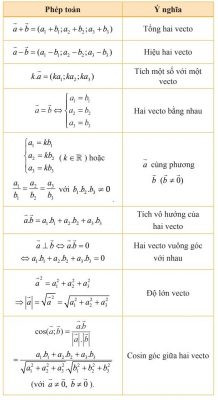
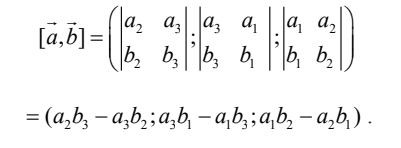 Tích có hướng của hai vectơ
Tích có hướng của hai vectơ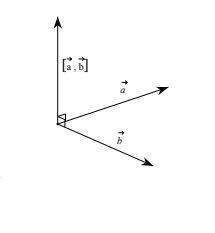 Tính chất tích có hướng của hai vectơ
Tính chất tích có hướng của hai vectơ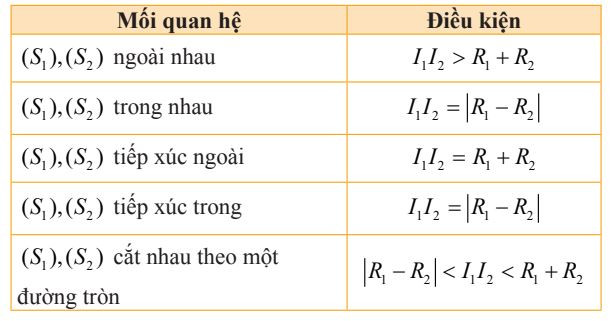 Vị trí tương đối của hai mặt cầu
Vị trí tương đối của hai mặt cầu Bài tập hệ tọa độ trong không gian
Bài tập hệ tọa độ trong không gian
 Đáp án hệ phương trình
Đáp án hệ phương trình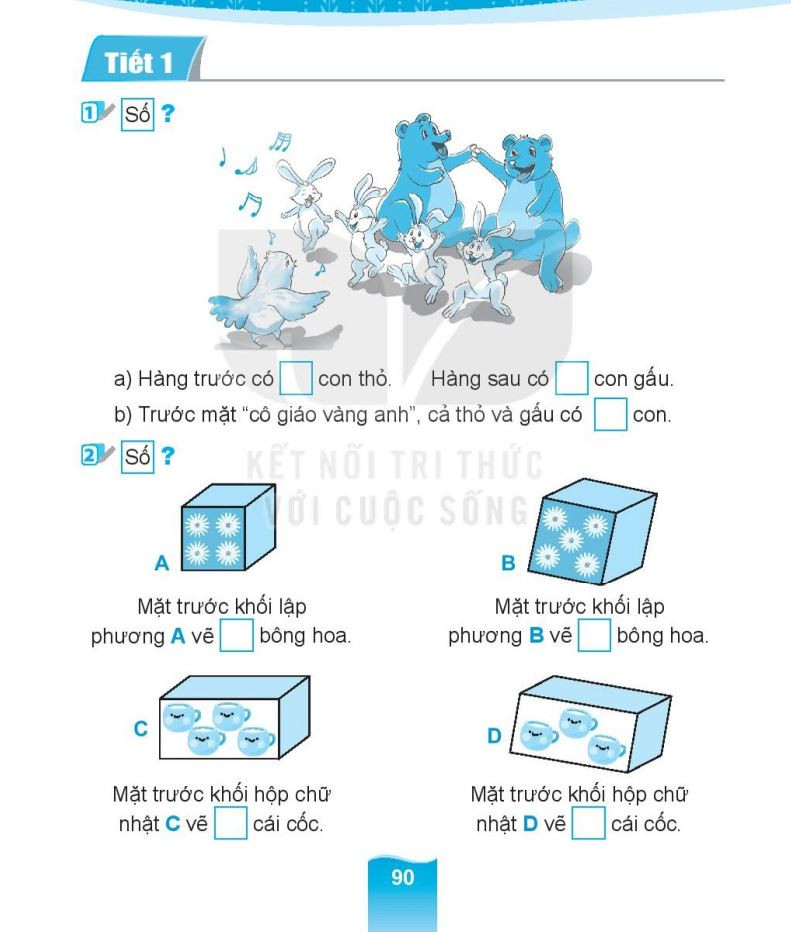
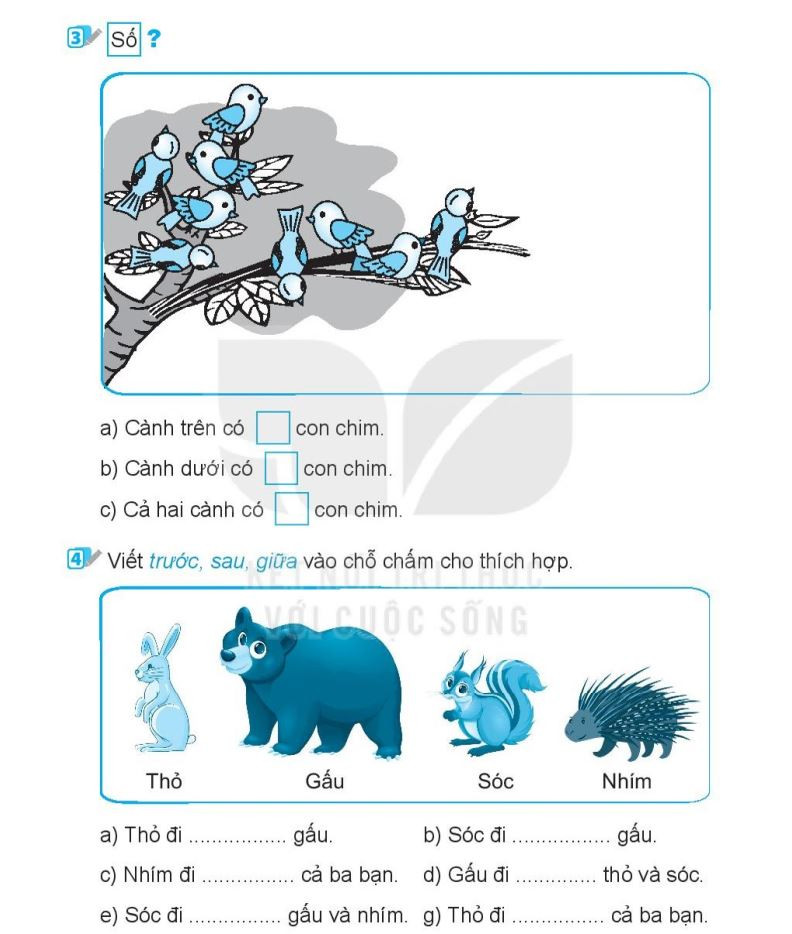 Bài tập xác định vị trí trong không gian lớp 1 – File 2
Bài tập xác định vị trí trong không gian lớp 1 – File 2 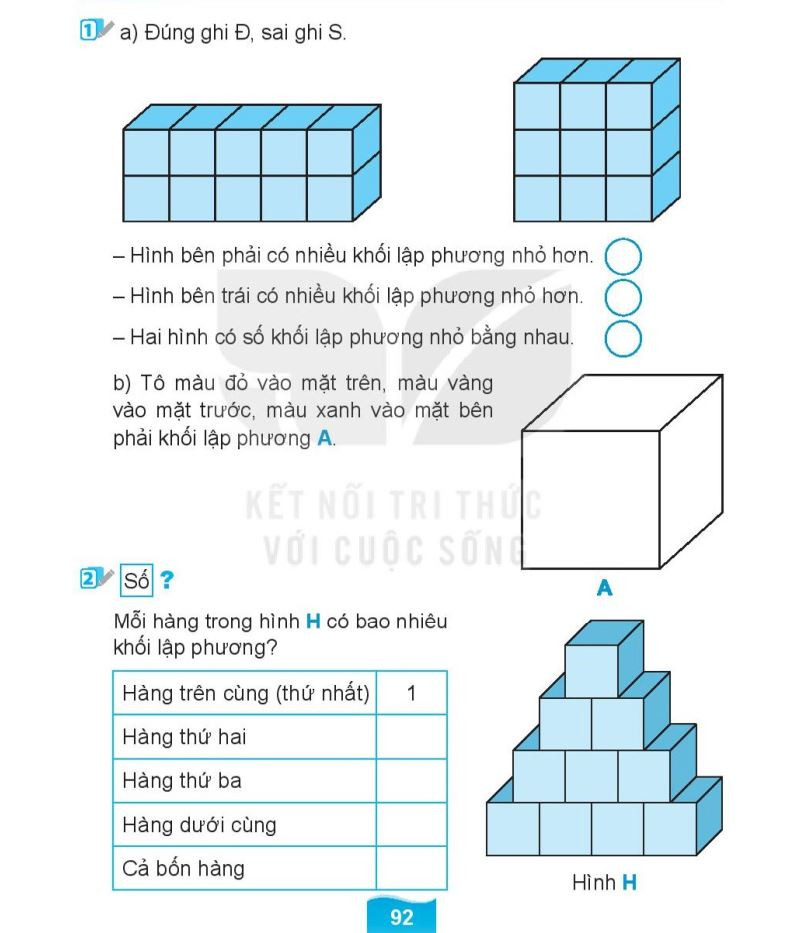 Bài tập xác định vị trí trong không gian lớp 1 – File 3
Bài tập xác định vị trí trong không gian lớp 1 – File 3  Bài tập xác định vị trí trong không gian lớp 1 – File 4
Bài tập xác định vị trí trong không gian lớp 1 – File 4 
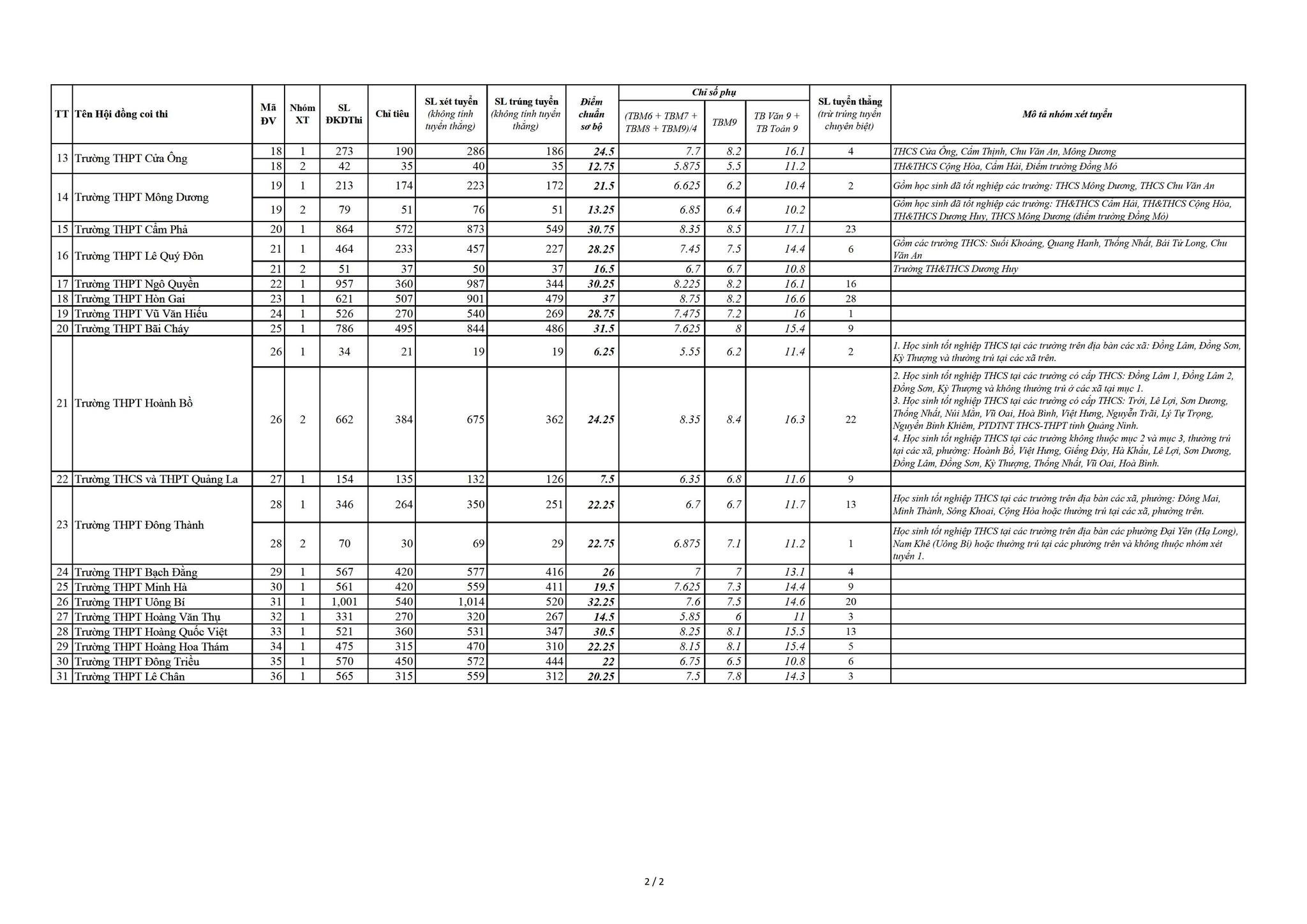 Điểm chuẩn trường THPT Hòn Gai năm 2024 – 2025
Điểm chuẩn trường THPT Hòn Gai năm 2024 – 2025
 Hình minh họa bài số 11 – Bài tập trắc nghiệmTrong hình vẽ trên có:
Hình minh họa bài số 11 – Bài tập trắc nghiệmTrong hình vẽ trên có: Hình minh họa bài số 15 – Bài tập trắc nghiệmA. 5 góc nhọn
Hình minh họa bài số 15 – Bài tập trắc nghiệmA. 5 góc nhọn Hình minh họa bài số 16 – Bài tập trắc nghiệmA. 3 góc nhọn
Hình minh họa bài số 16 – Bài tập trắc nghiệmA. 3 góc nhọn Hình minh họa bài số 17 – Bài tập trắc nghiệm
Hình minh họa bài số 17 – Bài tập trắc nghiệm Hình ảnh minh họa bài 1 – Bài tập tự luậna. Hình trên có ….. góc nhọn
Hình ảnh minh họa bài 1 – Bài tập tự luậna. Hình trên có ….. góc nhọn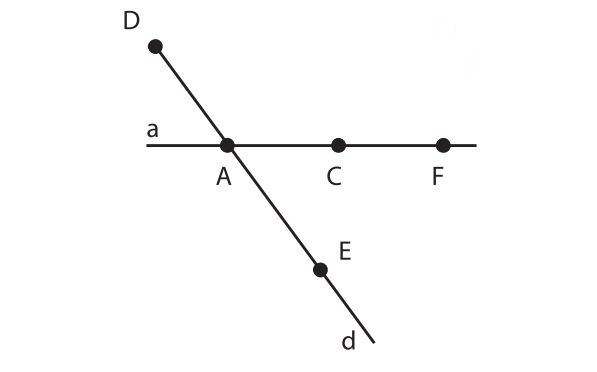
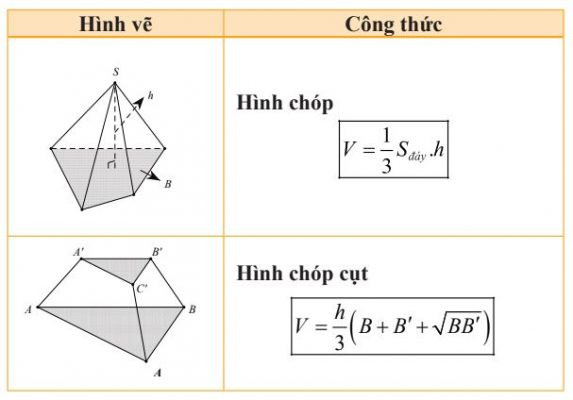
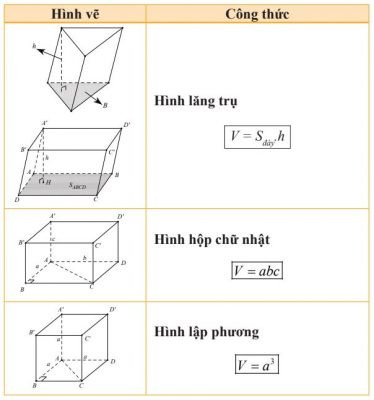 Công thức tính thể tích cơ bản (tiếp theo)
Công thức tính thể tích cơ bản (tiếp theo)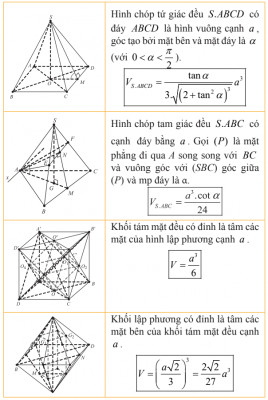 Công thức tính nhanh thể tích một số hình khối thường gặp (tiếp)
Công thức tính nhanh thể tích một số hình khối thường gặp (tiếp) Bài tập ví dụ về tính thể tích khối chóp
Bài tập ví dụ về tính thể tích khối chóp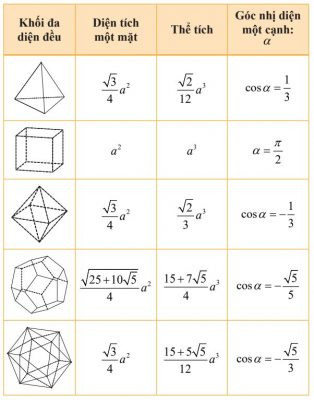 Một số kết quả của các khối đa diện đều đặc biệt
Một số kết quả của các khối đa diện đều đặc biệt  Công thức tính nhanh thể tích một số khối tứ diện đều đặc biệt (tiếp theo)
Công thức tính nhanh thể tích một số khối tứ diện đều đặc biệt (tiếp theo)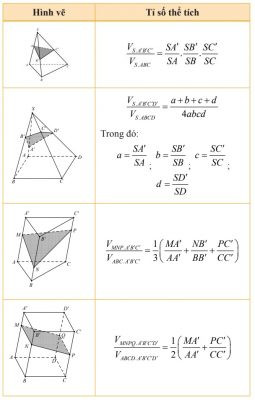 Tỷ số thể tích
Tỷ số thể tích Bài tập về thể tích khối đa diện
Bài tập về thể tích khối đa diện