Bài viết này sẽ cung cấp cho các em học sinh lớp 8 những kiến thức cơ bản về đơn thức, kèm theo các dạng toán phổ biến và hướng dẫn giải chi tiết, giúp các em nắm vững và tự tin hơn trong việc giải quyết các bài tập khó.
I. Ôn tập lý thuyết về đơn thức
1. Đơn thức
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc có dạng tích của những số và biến.
Ví dụ: (x^2y), (0), (3xy^2) là các đơn thức.
Lưu ý: (x + 5y), (xsqrt{y}) không phải là đơn thức.
Lý thuyết về đơn thức
2. Đơn thức thu gọn
Đơn thức thu gọn là đơn thức chỉ gồm một số, hoặc có dạng tích của một số với những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số nguyên dương.
Ví dụ: (A = -7x^2y^3z) là đơn thức thu gọn, (B = -7xy(-3)x^2) là đơn thức chưa thu gọn.
- Các đơn thức chưa thu gọn có thể thu gọn bằng cách áp dụng các tính chất của phép nhân và phép nâng lũy thừa.
Ví dụ: (B = -7xy(-3)x^2 = (-7)(-3)(x cdot x^2)y = 21x^3y).
- Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.
Ví dụ: Đơn thức (A = -7x^2y^3z) có tổng số mũ là: (2 + 3 + 1 = 6) nên (A) có bậc là 6.
3. Đơn thức đồng dạng
Hai đơn thức đồng dạng là hai đơn thức với hệ số khác 0 và có phần biến giống nhau.
- Hai đơn thức đồng dạng thì có cùng bậc.
Ví dụ: (A = 2x^2y^3); (B = -frac{1}{2}x^2y^3) là hai đơn thức đồng dạng.
4. Cộng/trừ đơn thức đồng dạng
Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
Ví dụ: Tính (A + B) biết (A = 2x^2y^3); (B = -frac{1}{2}x^2y^3).
Hướng dẫn giải:
[
A + B = -frac{1}{2}x^2y^3 + (-frac{1}{2}x^2y^3) = left(2 + (-frac{1}{2})right)x^2y^3 = frac{3}{2}x^2y^3.
]
II. Các dạng toán về đơn thức
1. Dạng toán nhận biết đơn thức
+ Phương pháp giải
Để nhận biết một biểu thức là đơn thức, ta cần căn cứ vào định nghĩa đơn thức (một số, một biến hoặc một tích giữa các số và các biến).
+ Các ví dụ
Ví dụ 1:
Trong các biểu thức sau, biểu thức nào là đơn thức?
- a) (2x^3y^2).
- b) (9 + yz^2).
- c) (x^2 – 3xy).
- d) (16,5ysqrt{3}).
- e) (x^2 – y^2).
- f) ((xyz)^3).
Hướng dẫn giải
Các đơn thức là: (2x^3y^2); ((xyz)^3).
Ví dụ 2:
Trong các biểu thức sau, biểu thức nào không phải là đơn thức?
- a) (12x + xz – yz).
- b) (0 cdot xy^2).
- c) (x^2 + y^2 + z^2).
- d) (3xz + yx^2 + z^2).
Hướng dẫn giải
Các biểu thức không phải là đơn thức: (12x + xz – yz); (x^2 + y^2 + z^2); (3xz + yx^2 + z^2).
2. Dạng toán thu gọn đơn thức
+ Phương pháp giải
Để nhân hai hay nhiều đơn thức, ta nhân hệ số với nhau và nhân các phần biến với nhau.
Khi viết một đơn thức thành một đơn thức thu gọn, ta cũng sử dụng quy tắc nhân đơn thức nêu trên.
+ Ví dụ
Ví dụ 1:
Thu gọn các đơn thức sau:
- a) (frac{4}{3}xy cdot frac{9}{2}x^2y^3)
- b) (5xy^3 cdot (-0,4xy^3))
- c) ((-0,1x^2z) cdot (-3z^3x^3))
Hướng dẫn giải
-
a) (frac{4}{3}xy cdot frac{9}{2}x^2y^3 = frac{4}{3} cdot frac{9}{2} cdot (x cdot x^2) cdot (y cdot y^3) = 6x^3y^4).
-
b) (5xy^3 cdot (-0,4xy^3) = 5 cdot (-0,4) cdot (x cdot x) cdot (y^3 cdot y^3) = -2x^2y^6).
-
c) ((-0,1x^2z) cdot (-3z^3x^3) = (-0,1) cdot (-3) cdot (x^2 cdot x^3) cdot (z cdot z^3) = 0,3x^5z^4).
3. Dạng toán tính giá trị của đơn thức
+ Phương pháp giải
Thay giá trị của các biến vào đơn thức rồi thực hiện các phép tính.
+ Các ví dụ
Ví dụ 1:
Cho đơn thức (A = 2023x^3y^2).
- a) Xác định phần hệ số, phần biến của (A).
- b) Tính giá trị của đơn thức (A) tại (x = 2) và (y = -1).
Hướng dẫn giải
-
a) (A) có phần hệ số là (2023); phần biến là (x^3y^2).
-
b) Tại (x = 2) và (y = -1), ta có (A = 2023 cdot 2^3 cdot (-1)^2 = 2023 cdot 8 cdot 1 = 16184).
Ví dụ 2:
Tại giá trị nào của (x), thì đơn thức (4xy^3) có giá trị là (-64), biết rằng (y = -2).
Hướng dẫn giải
Ta có:
[
4xy^3 = -64
]
(y = -2 Rightarrow 4x(-2)^3 = -64) Rightarrow (4x cdot (-8) = -64) Rightarrow (x = 2).
4. Dạng toán nhận biết đơn thức đồng dạng
+ Phương pháp
Dựa vào dấu hiệu:
- Hệ số khác 0;
- Có cùng phần biến.
+ Các ví dụ
Ví dụ 1:
Sắp xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng: (frac{2023}{3}x^2y; -frac{2}{3}xy^2; frac{7}{3}x^2y; 4x^2y; frac{1}{4}xy^2; x^2y^2)
Hướng dẫn giải
Các nhóm đơn thức đồng dạng là:
- Nhóm 1: (frac{2023}{3}x^2y; frac{7}{3}x^2y; 4x^2y)
- Nhóm 2: (-frac{2}{3}xy^2; frac{1}{4}xy^2)
Còn lại (x^2y^2) không đồng dạng với các đơn thức đã cho.
Ví dụ 2:
Chứng tỏ rằng các đơn thức sau là đơn thức đồng dạng:
- (A = 9x^3y cdot frac{1}{27}x^4y^2)
- (B = frac{1}{4}(x^2y)^2 cdot frac{2}{5}x^3y)
Hướng dẫn giải
(A = 9x^3y cdot frac{1}{27}x^4y^2 = frac{-1}{3}x^7y^3).
(B = frac{1}{4}(x^2y)^2 cdot frac{2}{5}x^3y = frac{1}{10}x^7y^3).
Vậy các đơn thức đã cho là đồng dạng với nhau.
5. Dạng toán cộng/trừ các đơn thức đồng dạng
+ Phương pháp giải
Cộng hay trừ các hệ số và giữ nguyên phần biến.
+ Các ví dụ
Ví dụ 1:
Cho các đơn thức (A = 2x^2y; B = -3x^2y) và (C = 5x^2y) là ba đơn thức đồng dạng.
- Tính (A + B); (A – B); (A + B + C).
Hướng dẫn giải
-
(A + B = [2 + (-3)]x^2y = -x^2y)
-
(A – B = [2 – (-3)]x^2y = 5x^2y)
-
(A + B + C = (2 – 3 + 5)x^2y = 4x^2y).
Ví dụ 2:
Thu gọn biểu thức sau:
- a) (-5y^2 – 0.2y^2 + 3.2y^2);
- b) (7m^3 – 5m^2 + 2m – 3m^3 – 9m^2 – 3m).
Hướng dẫn giải
-
a) (-5y^2 – 0.2y^2 + 3.2y^2 = (-5 – 0.2 + 3.2)y^2 = -2y^2)
-
b) (7m^3 – 5m^2 + 2m – 3m^3 – 9m^2 – 3m = (7 – 3)m^3 – (5 + 9)m^2 + (2 – 3)m = 4m^3 – 14m^2 – m).
6. Dạng toán về đơn thức có yếu tố hình học
+ Phương pháp
Vận dụng cách tính diện tích của các hình thường gặp
Lập biểu thức là các đơn thức đồng dạng.
+ Ví dụ
Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến (x) và (y) biểu thị diện tích của mảnh đất đã cho bằng hai cách:
- Cách 1. Tính tổng diện tích của hai hình chữ nhật ANHD và MECH.
- Cách 2. Lấy diện tích của hình chữ nhật ABCD trừ đi diện tích của hình chữ nhật BEMN.
Hướng dẫn giải
- Cách 1:
Diện tích của hình chữ nhật ANHD: (S_{ANHD} = AD cdot DH = 4x cdot 4y = 16xy).
Diện tích của hình chữ nhật MECH : (S_{MECH} = EC cdot CH = 3x cdot 3y = 9xy).
Diện tích của mảnh đất đã cho: (S = S{ANHD} + S{MECH} = 16xy + 9xy = 25xy).
- Cách 2:
Diện tích của hình chữ nhật ABCD: (S_{ABCD} = AD cdot CD = 4x cdot 7y = 28xy).
Diện tích của hình chữ nhật BEMN: (S_{BEMN} = BE cdot EM = (BC – EC) cdot EM = (4x – 3x)3y = 3xy).
Diện tích của mảnh đất đã cho: (S{ABCD} – S{BEMN} = 28xy – 3xy = 25xy).
Hy vọng qua bài viết “Toán lớp 8 bài 1: Đơn thức – Các dạng toán kèm lời giải chi tiết nhất,” các em đã hiểu rõ hơn về khái niệm đơn thức và biết cách giải quyết các dạng bài tập liên quan đến đơn thức một cách hiệu quả.
Các dạng toán và lý thuyết ở trên đều có sẵn trong cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 8 – Tập 1. Các em nên mua cuốn sách này để hỗ trợ cho việc học Toán của mình nhé! Ngoài ra TKbooks cũng có đủ bộ sách tham khảo lớp 8 của môn Ngữ Văn và Tiếng Anh với nội dung bám sát chương trình học mới nhất.
Link đọc thử sách: https://drive.google.com/file/d/1TsmoDs83uAwQu0FqU6ikrzFtEBDMH2Kq/view
TKbooks tự hào là nhà xuất bản sách tham khảo lớp 8 hàng đầu tại Việt Nam!
TKbooks.vn
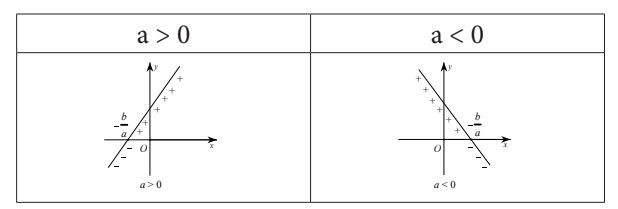Minh họa bằng đồ thị dấu của nhị thức bậc nhất
Ví dụ về bất phương trình chứa ẩn ở mẫu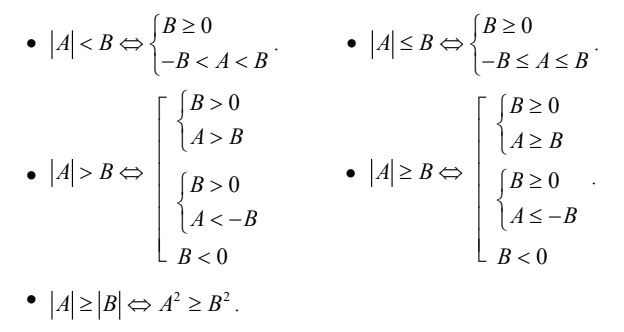
Bất phương trình chứa dấu giá trị tuyệt đối
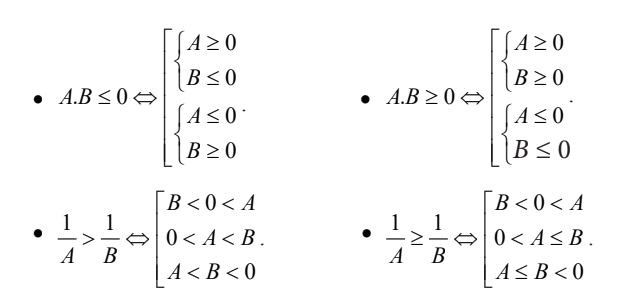Các bất phương trình khác
Ví dụ về bất phương trình bậc nhất hai ẩn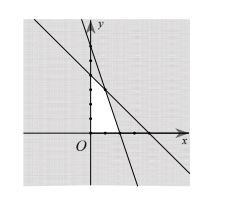
Đồ thị miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
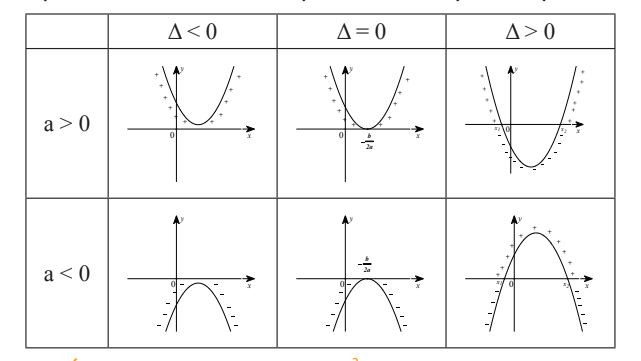Minh họa hình học về dấu của tam thức bậc 2
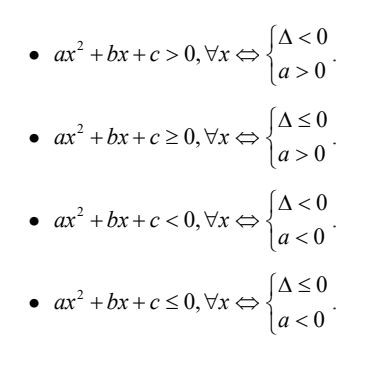Điều kiện tương đương của bất phương trình bậc 2 một ẩn
Bài tập bất đẳng thức và bất phương trình
Bài tập bất đẳng thức và bất phương trình (tiếp theo)
Ví dụ về hệ phương trình
Sổ Tay Kiến Thức Toán Văn Anh Lớp 6
Cuốn Sách Tổng Hợp Kiến Thức và Bài Tập Tiếng Anh Lớp 6
Cuốn Sách Trọng Tâm Kiến Thức và Bài Tập Tiếng Anh Lớp 6
Cuốn Sách Sổ Tay Tiếng Anh Lớp 6
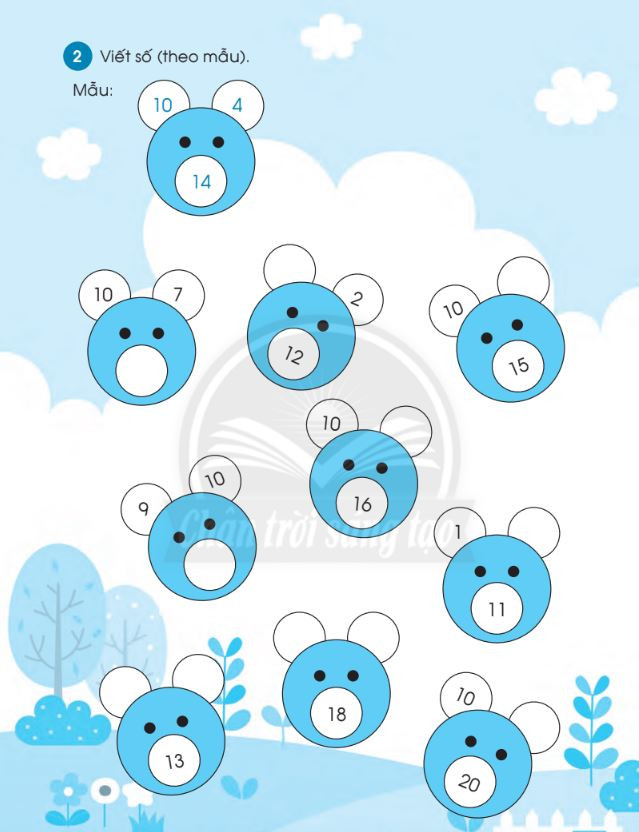Bài tập nhận biết các số trong phạm vi 20 – File 2
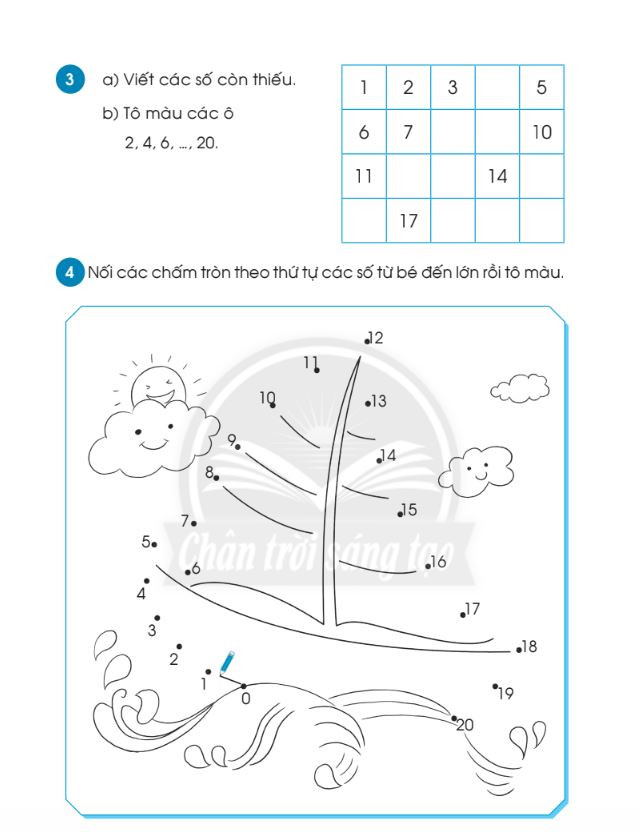Bài tập nhận biết các số trong phạm vi 20 – File 3
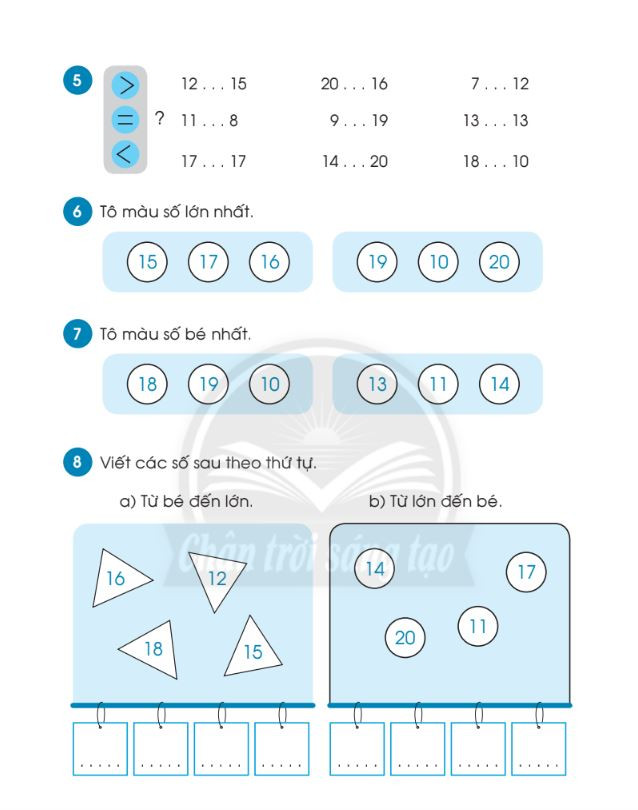Bài tập nhận biết các số trong phạm vi 20 – File 4
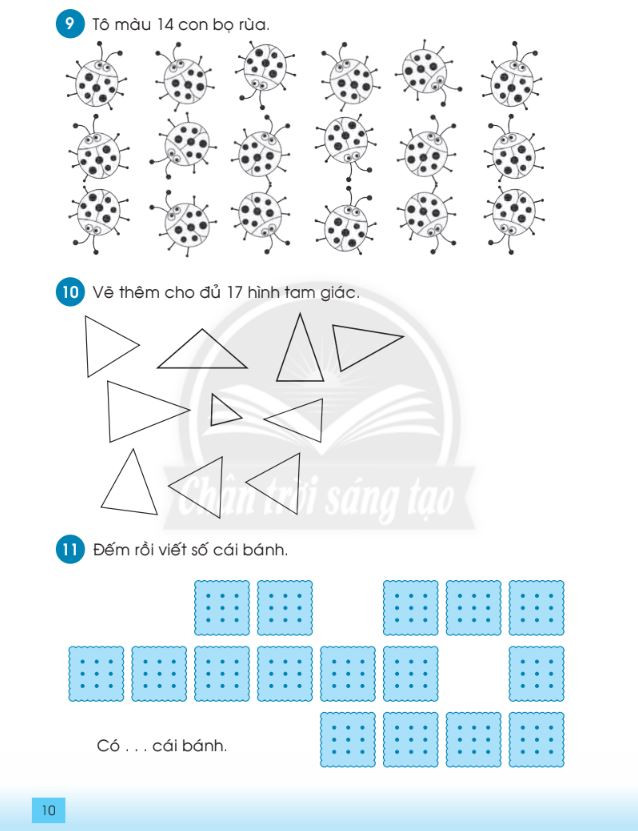Bài tập nhận biết các số trong phạm vi 20 – File 5
Bài tập nhận biết các số trong phạm vi 20 – File 6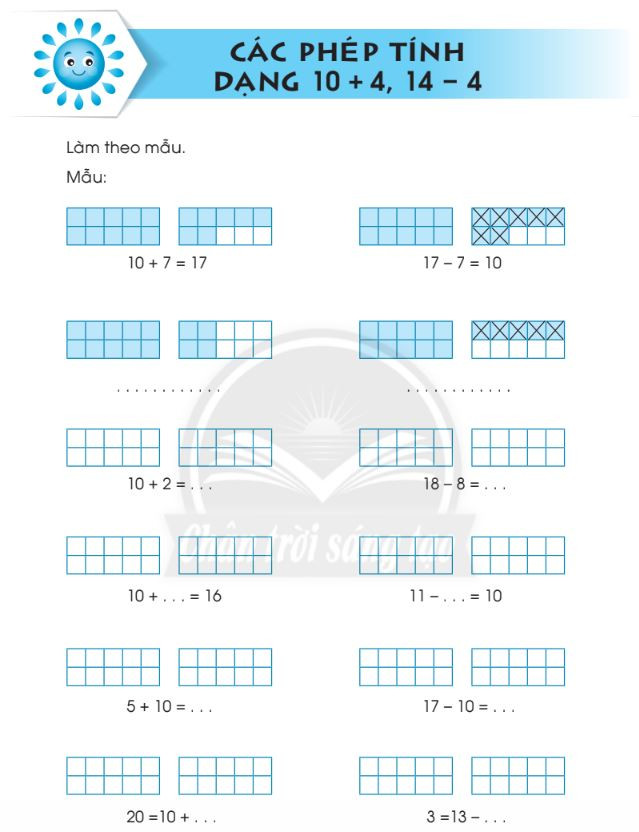
Các phép tính dạng 10 + 4; 14 – 4 trong phạm vi 20
Các phép tính dạng 12 + 3; 15 – 3 trong phạm vi 20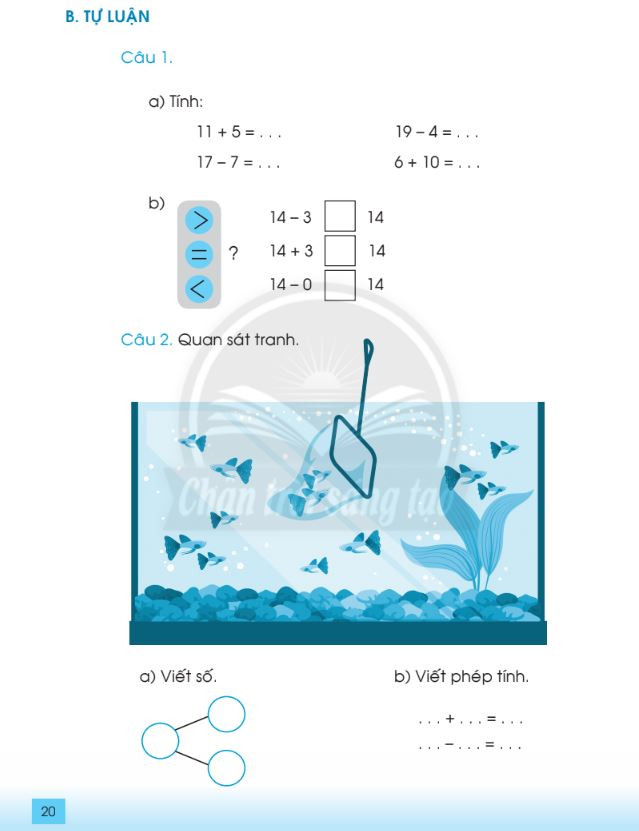
Bài tập luyện tập chung trong phạm vi 20 lớp 1
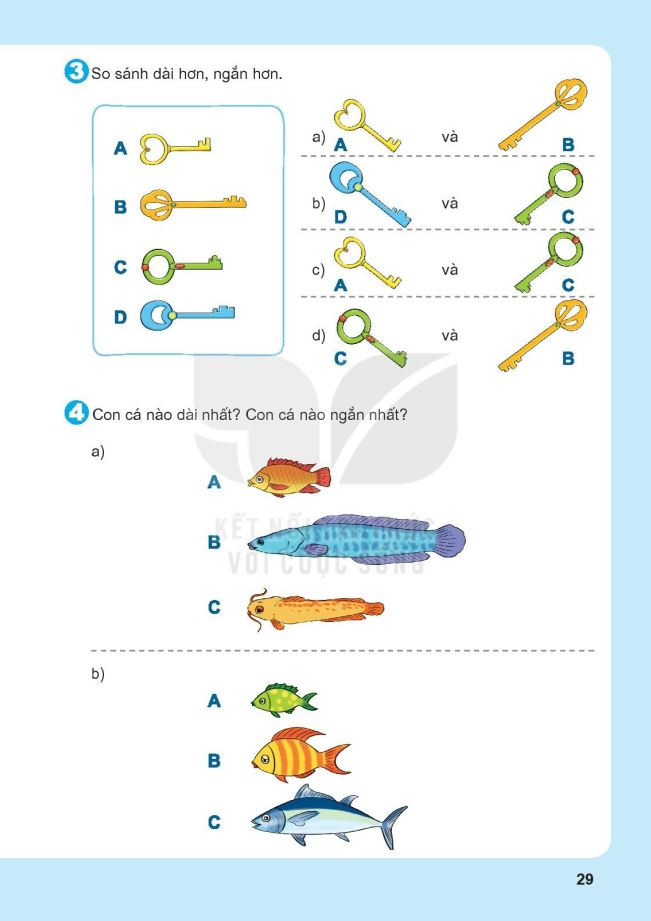Bài tập so sánh độ dài lớp 1 – File 2
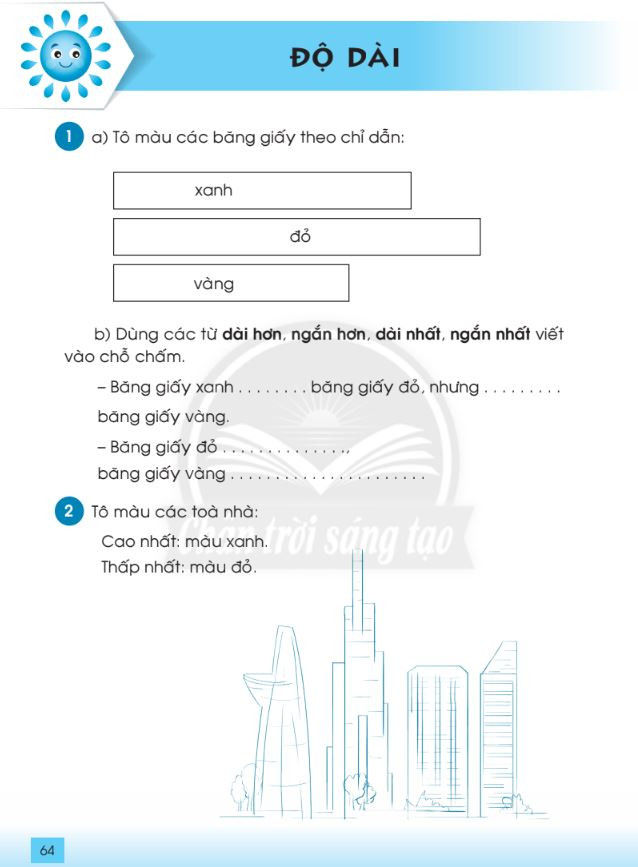Bài tập so sánh độ dài lớp 1 – File 3
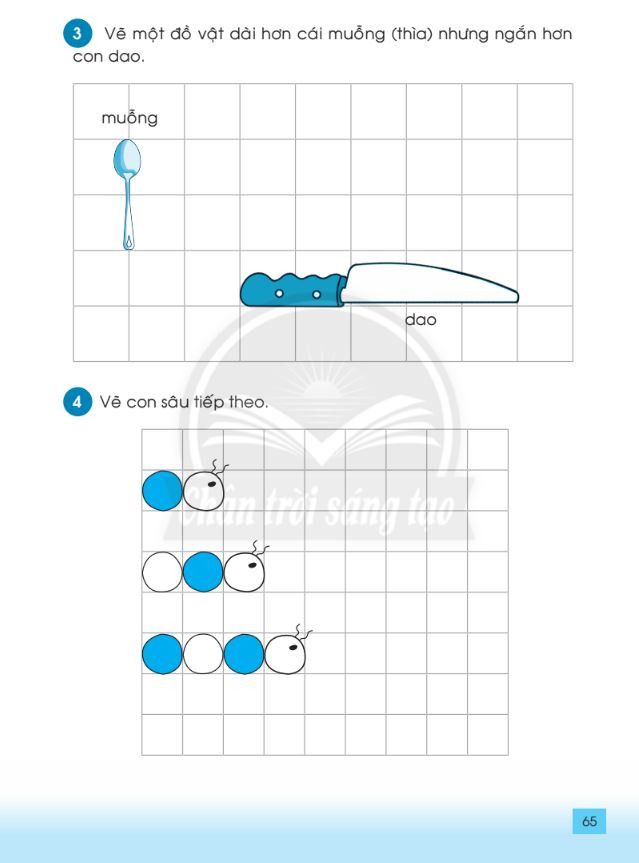Bài tập so sánh độ dài lớp 1 – File 4
Giải thích cho bé hiểu về độ dài