Hình thang vuông là một hình dạng đặc biệt của hình thang, được nhận diện bởi một gốc vuông và hai cạnh đáy không song song. Việc tính diện tích hình thang vuông cũng tương tự như hình thang thường, tuy nhiên, với tính chất đặc biệt này, chúng ta cần lưu ý một số điều khi tiến hành tính toán.
Hãy cùng khám phá cách tính diện tích hình thang vuông qua bài viết sau đây nhé!
I. Quy Tắc Tính
Để tính diện tích hình thang vuông, ta áp dụng công thức tính diện tích hình thang như sau:
| 📝 Công thức: S = [(a + b) × h] / 2 |
|---|
Trong đó:
- ✅ S là diện tích hình thang vuông.
- ✅ a là độ dài đáy lớn.
- ✅ b là độ dài đáy nhỏ.
- ✅ h là chiều cao của hình thang vuông (chính là cạnh vuông góc với hai đáy).
📝 Quy Tắc:
- 📏 Cộng độ dài hai đáy của hình thang vuông.
- 📏 Nhân tổng đó với chiều cao.
- 📏 Chia kết quả cho 2 để tìm diện tích.
📝 Ví dụ:
Cho một hình thang vuông có đáy lớn là 10 cm, đáy nhỏ là 6 cm và chiều cao 4 cm.
Diện tích của nó là:
S = [(10 + 6) × 4] / 2 = (16 × 4)/2 = 64/2 = 32 cm².
✅ Kết quả: Diện tích hình thang vuông là 32 cm².
II. Bài Tập Vận Dụng
🔹 Bài 1: Một khu đất hình thang vuông có đáy lớn là 65 m, đáy nhỏ là 45 m. Nếu mở rộng thành khu đất hình chữ nhật nhưng vẫn giữ nguyên đáy lớn và chiều cao thì diện tích khu đất tăng thêm 1000 m². Hãy tính diện tích hình thang vuông ban đầu?
🔹 Bài 2: Cho hình thang ABCD vuông tại A và D có AB = 3 cm; AD = 7 cm; CD = 10 cm. Tính diện tích hình thang ABCD.
🔹 Bài 3: Cho hình thang vuông ABCD có AB = 30 cm; AD = 25 cm; CD = 50 cm. Tính diện tích hình thang vuông ABCD.
Hình minh họa bài 3:
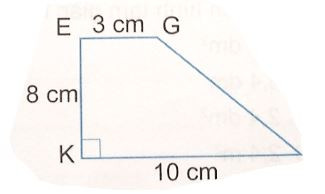 Hình minh họa bài 3
Hình minh họa bài 3
🔹 Bài 4: Tính diện tích hình thang dưới đây:
🔹 Bài 5: Một sân trường có dạng hình chữ nhật với chiều dài 30 m và chiều rộng 20 m. Trong sân có một khu vực trồng cây hình thang vuông với đáy lớn 12 m, đáy nhỏ 8 m và chiều cao 10 m. Tính diện tích phần sân còn lại sau khi đã trừ đi khu vực trồng cây.
🔹 Bài 6: Mái của một ngôi nhà có dạng hai hình thang vuông ghép lại. Mỗi hình thang vuông có đáy lớn 4,5 m, đáy nhỏ 3 m và chiều cao 2 m. Hãy tính tổng diện tích của mái nhà.
🔹 Bài 7: Một tấm vải hình chữ nhật có kích thước 1,2 m x 1 m được cắt thành hai phần: một hình chữ nhật nhỡ và một hình thang vuông. Hình chữ nhật nhỡ có chiều rộng 0,5 m và chiều dài bằng chiều cao của hình thang vuông. Biết rằng đáy lớn của hình thang vuông là 1,2 m, hãy tính diện tích phần hình thang vuông còn lại.
Hy vọng bài viết trên đã giúp bạn nắm vững quy tắc và áp dụng vào bài tập một cách dễ dàng! Các bài tập trên đều có trong cuốn 50 Đề Tăng Điểm Nhanh Toán Lớp 5. Quý phụ huynh hãy mua ngay cuốn sách này để giúp con học tốt môn Toán hơn nhé!
Link đọc thử sách: https://drive.google.com/file/d/1bD2vpRYqsx_Sqyi5Ww72Bgb4i58BrziO/view
Link đặt mua sách với giá ưu đãi: https://luyende.tkbooks.vn/lop5
Tkbooks tự hào là nhà xuất bản sách tham khảo lớp 5 hàng đầu tại Việt Nam!

 Cuốn sách Vừa Lười Vừa Bạn Văn Giỏi Tiếng Anh
Cuốn sách Vừa Lười Vừa Bạn Văn Giỏi Tiếng Anh Bộ tài liệu chuẩn giúp bạn học từ vựng hữu ích cho giao tiếp
Bộ tài liệu chuẩn giúp bạn học từ vựng hữu ích cho giao tiếp
 Bộ sách công phá các môn học 10 cần thiết trong hành trang kiến thức của học sinh
Bộ sách công phá các môn học 10 cần thiết trong hành trang kiến thức của học sinh Bộ sách đột phá tư duy bồi dưỡng học sinh giỏi 10
Bộ sách đột phá tư duy bồi dưỡng học sinh giỏi 10 Bộ sách tự học tham khảo lớp 10 hữu ích cho các em
Bộ sách tự học tham khảo lớp 10 hữu ích cho các em

 Sổ tay kèm theo sách
Sổ tay kèm theo sách

 Bộ sách Đề kiểm tra Tiếng Việt 3
Bộ sách Đề kiểm tra Tiếng Việt 3  Bộ sách Bài tập hàng ngày Tiếng Việt lớp 3
Bộ sách Bài tập hàng ngày Tiếng Việt lớp 3  Cuốn sách Hướng dẫn cách viết Tập làm văn 3
Cuốn sách Hướng dẫn cách viết Tập làm văn 3  Cuốn sách Chinh phục nâng cao Tiếng Việt lớp 3
Cuốn sách Chinh phục nâng cao Tiếng Việt lớp 3 
 Đề thi Toán THPT Quốc Gia năm 2024 – Trang 1
Đề thi Toán THPT Quốc Gia năm 2024 – Trang 1 Đề thi Toán THPT Quốc Gia năm 2024 – Trang 2
Đề thi Toán THPT Quốc Gia năm 2024 – Trang 2 Đề thi Toán THPT Quốc Gia năm 2024 – Trang 3
Đề thi Toán THPT Quốc Gia năm 2024 – Trang 3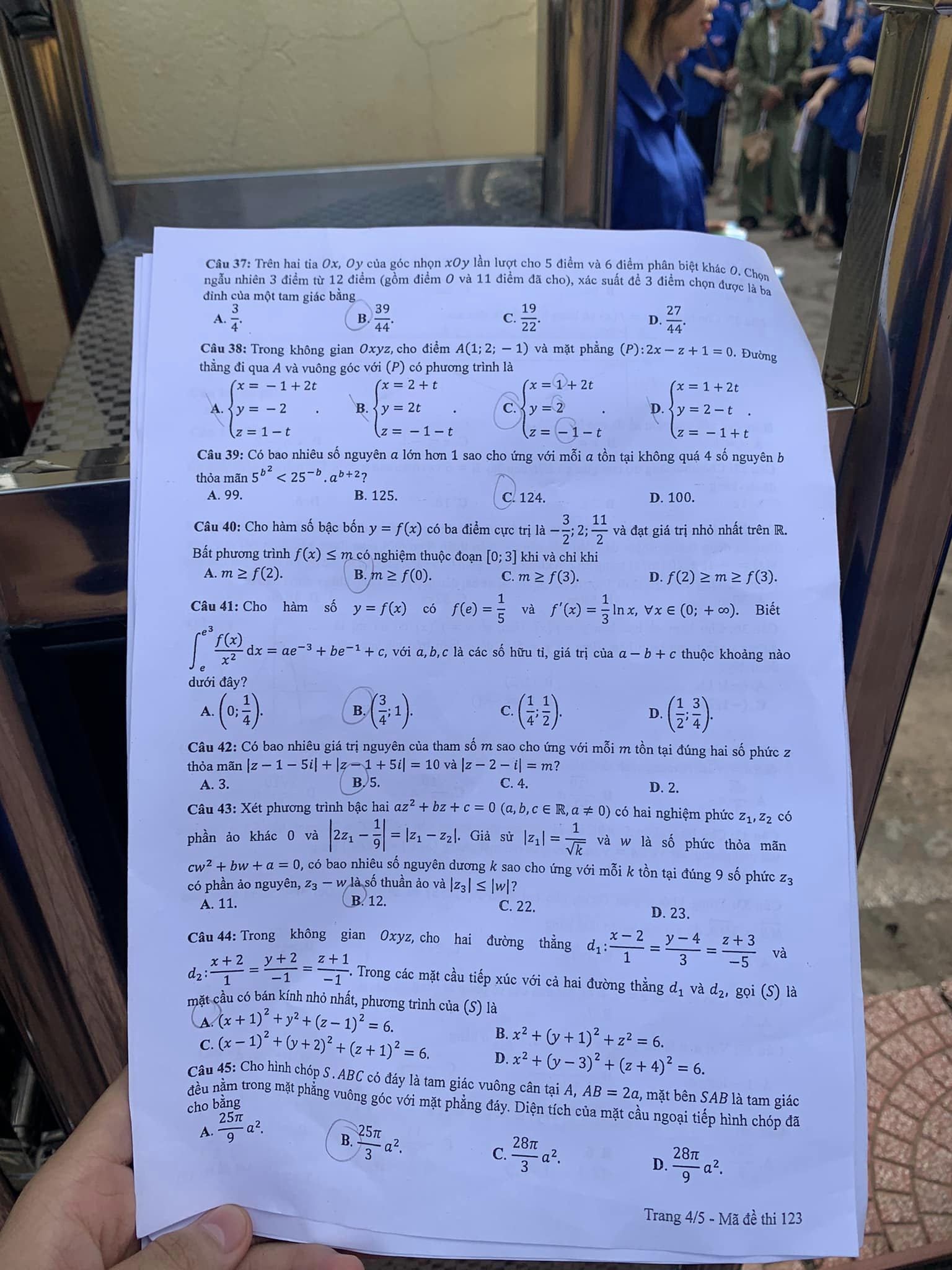 Đề thi Toán THPT Quốc Gia năm 2024 – Trang 4
Đề thi Toán THPT Quốc Gia năm 2024 – Trang 4 Đề thi Toán THPT Quốc Gia năm 2024 – Trang 5
Đề thi Toán THPT Quốc Gia năm 2024 – Trang 5 
 File bài tập số 2
File bài tập số 2 File bài tập số 3
File bài tập số 3 File bài tập số 4
File bài tập số 4 File bài tập số 5
File bài tập số 5 File bài tập số 6
File bài tập số 6 File bài tập số 7
File bài tập số 7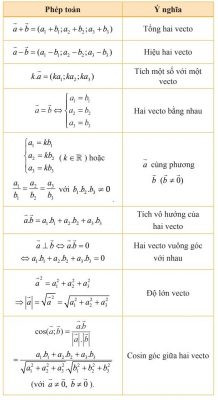
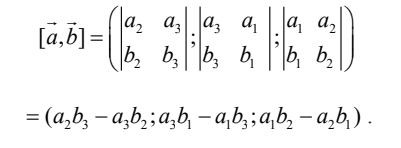 Tích có hướng của hai vectơ
Tích có hướng của hai vectơ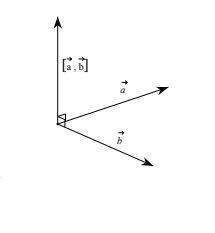 Tính chất tích có hướng của hai vectơ
Tính chất tích có hướng của hai vectơ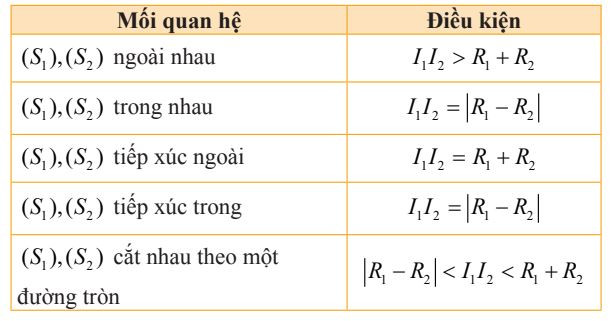 Vị trí tương đối của hai mặt cầu
Vị trí tương đối của hai mặt cầu Bài tập hệ tọa độ trong không gian
Bài tập hệ tọa độ trong không gian