Dưới đây là danh sách các trường THPT dân lập tại Long Biên, đi kèm với mức học phí, địa chỉ, thông tin tuyển sinh và các giấy tờ cần thiết để nộp hồ sơ.
1. Trường THPT dân lập Đông Kinh
Địa chỉ: Số 2, Ngõ 3, Phố Đông Thiên, Phường Vĩnh Hưng, Quận Hoàng Mai, Hà Nội
- Mức học phí năm 2023 – 2024: 4,5 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường THPT dân lập Đông Kinh
Trường THPT dân lập Đông Kinh
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Trường Đông Kinh nổi bật với chương trình giảng dạy kết hợp giữa kiến thức phổ thông và các hoạt động ngoại khóa phong phú, giúp học sinh phát triển toàn diện.
Website của trường: http://thptdongkinh.edu.vn/
2. Trường THPT dân lập Lê Văn Thiêm – Long Biên
Địa chỉ: Số 25, Ngõ 12, Phố Ngọc Thụy, Phường Ngọc Thụy, Quận Long Biên, Hà Nội
- Mức học phí năm 2023 – 2024: 4,8 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường THPT dân lập Lê Văn Thiêm
Trường THPT dân lập Lê Văn Thiêm
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Lê Văn Thiêm là trường THPT dân lập nổi tiếng với đội ngũ giáo viên nhiệt tình, giàu kinh nghiệm, và phương pháp giảng dạy hiện đại.
3. Trường THPT dân lập Đinh Tiên Hoàng Cơ sở 3 – Long Biên
Địa chỉ: Số 8, Ngõ 93, Phố Vũ Xuân Thiều, Phường Phúc Lợi, Quận Long Biên, Hà Nội
- Mức học phí năm 2023 – 2024: 4,7 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường THPT dân lập Đinh Tiên Hoàng Cơ sở 3
Trường THPT dân lập Đinh Tiên Hoàng Cơ sở 3
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Trường THPT Đinh Tiên Hoàng Cơ sở 3 nổi bật với môi trường học tập thân thiện, cơ sở vật chất khang trang và chương trình giáo dục tiên tiến.
4. Trường THPT dân lập Văn Xuân Long Biên
Địa chỉ: Số 45, Phố Phú Viên, Phường Bồ Đề, Quận Long Biên, Hà Nội
- Mức học phí năm 2023 – 2024: 4,9 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường THPT dân lập Văn Xuân
Trường THPT dân lập Văn Xuân
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Văn Xuân là trường THPT dân lập luôn chú trọng đến việc nâng cao chất lượng giáo dục và tạo điều kiện tốt nhất cho học sinh phát triển toàn diện.
5. Trường THPT Đào Duy Từ
Địa chỉ: Số 51, Phố Phú Gia, Phường Phúc Xá, Quận Ba Đình, Hà Nội
- Mức học phí năm 2023 – 2024: 4,6 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Trường THPT Đào Duy Từ cung cấp chương trình học đa dạng, giúp học sinh có nhiều lựa chọn phát triển theo hướng học thuật hoặc nghề nghiệp.
6. Trường Phổ thông Liên cấp Bảo Long – Long Biên
Địa chỉ: Số 19, Ngõ 75, Phố Gia Quất, Phường Thượng Thanh, Quận Long Biên, Hà Nội
- Mức học phí năm 2023 – 2024: 4,3 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường Phổ thông Liên cấp Bảo Long
Trường Phổ thông Liên cấp Bảo Long
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Trường Phổ thông Liên cấp Bảo Long nổi bật với chương trình giáo dục toàn diện, chú trọng đến sự phát triển cá nhân của từng học sinh.
7. Trường THCS & THPT Hồng Hà – Long Biên
Địa chỉ: Số 15, Ngõ 123, Phố Đúc Giang, Phường Đúc Giang, Quận Long Biên, Hà Nội
- Mức học phí năm 2023 – 2024: 4,4 triệu đồng/tháng
- Mức học phí dự kiến năm 2024 – 2025: Chưa có thông tin cập nhật
- Thời gian nộp hồ sơ: Từ 1/6/2024 đến 30/6/2024
 Trường THCS & THPT dân lập Hồng Hà
Trường THCS & THPT dân lập Hồng Hà
Thông tin tuyển sinh:
- Tuyển sinh dựa trên điểm thi vào lớp 10 hoặc học bạ THCS.
- Ưu tiên học sinh có thành tích tốt trong học tập và rèn luyện.
Cách thức nộp hồ sơ:
Phụ huynh và học sinh có thể nộp hồ sơ trực tiếp tại trường hoặc qua hệ thống tuyển sinh trực tuyến của trường.
Giấy tờ cần nộp:
- Đơn xin nhập học (theo mẫu của trường).
- Bản sao học bạ THCS.
- Bản sao giấy khai sinh.
- Giấy chứng nhận tốt nghiệp THCS tạm thời.
- Giấy chứng nhận điểm thi vào lớp 10 (nếu có).
Trường THCS & THPT Hồng Hà có môi trường học tập hiện đại, đội ngũ giáo viên chất lượng cao và chương trình học tập đa dạng.
Hy vọng với thông tin về các trường THPT dân lập ở Long Biên và khu vực gần Long Biên có mức học phí dưới 5 triệu đồng, phụ huynh sẽ có thêm lựa chọn hợp lý cho con em mình. Để biết thêm chi tiết về từng trường, phụ huynh có thể liên hệ trực tiếp với các trường hoặc truy cập website của trường để cập nhật thông tin mới nhất về học phí và chương trình học.

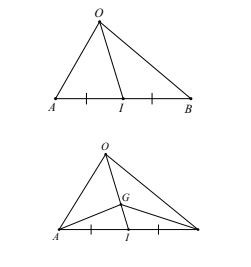 Hình minh họa cho ứng dụng của hiệu hai vecto
Hình minh họa cho ứng dụng của hiệu hai vecto Bài tập ví dụ về tích của vecto
Bài tập ví dụ về tích của vecto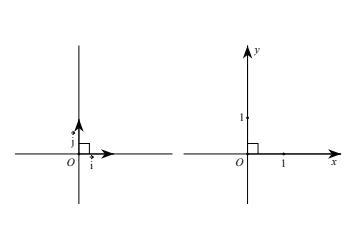 Mặt phẳng tọa độ Oxy
Mặt phẳng tọa độ Oxy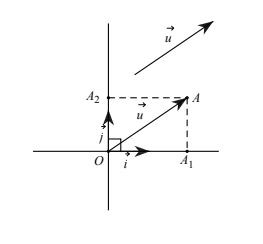 Cách xác định tọa độ của vecto
Cách xác định tọa độ của vecto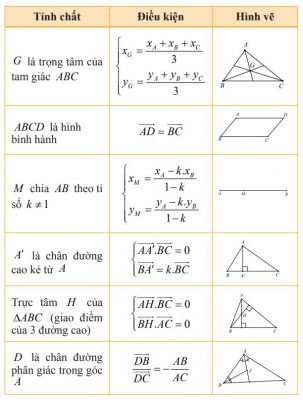 Một số điều kiện xác định điểm khác
Một số điều kiện xác định điểm khác Bài tập ví dụ về vecto
Bài tập ví dụ về vecto Bài tập ví dụ về vecto (tiếp theo)
Bài tập ví dụ về vecto (tiếp theo)
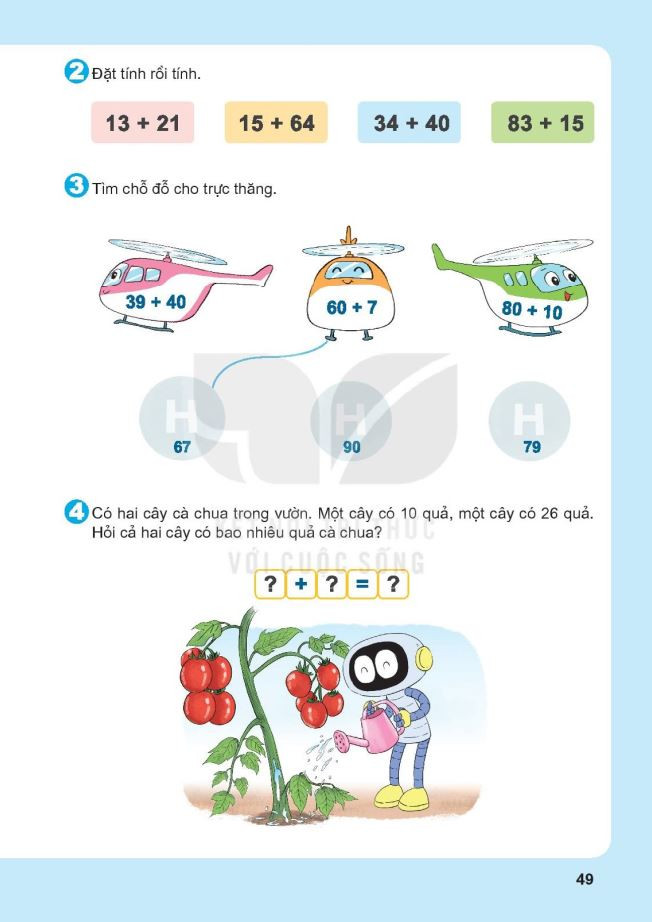 Bài tập phép cộng số có hai chữ số với số có hai chữ số
Bài tập phép cộng số có hai chữ số với số có hai chữ số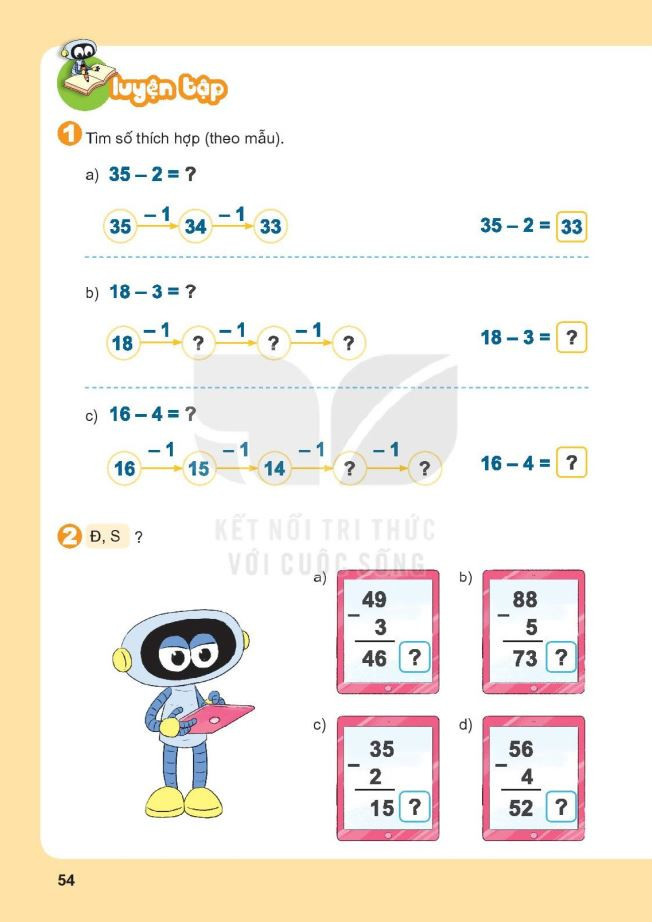 Bài tập phép trừ số có hai chữ số cho số có một chữ số
Bài tập phép trừ số có hai chữ số cho số có một chữ số
 Nội dung cuốn sách bám sát với đề thi THPT Quốc Gia
Nội dung cuốn sách bám sát với đề thi THPT Quốc Gia Các dạng bài tập trong sách được hệ thống đầy đủ theo logic từ dễ đến khó
Các dạng bài tập trong sách được hệ thống đầy đủ theo logic từ dễ đến khó Sách được tặng kèm phần audio để nghe lý thuyết một cách đơn giản và dễ thuộc
Sách được tặng kèm phần audio để nghe lý thuyết một cách đơn giản và dễ thuộc Tham gia nhóm facebook trao đổi, hỗ trợ học
Tham gia nhóm facebook trao đổi, hỗ trợ học
 Bài tập chép mẫu
Bài tập chép mẫu Dạng bài tập quan sát và viết mô tả bức tranh
Dạng bài tập quan sát và viết mô tả bức tranh
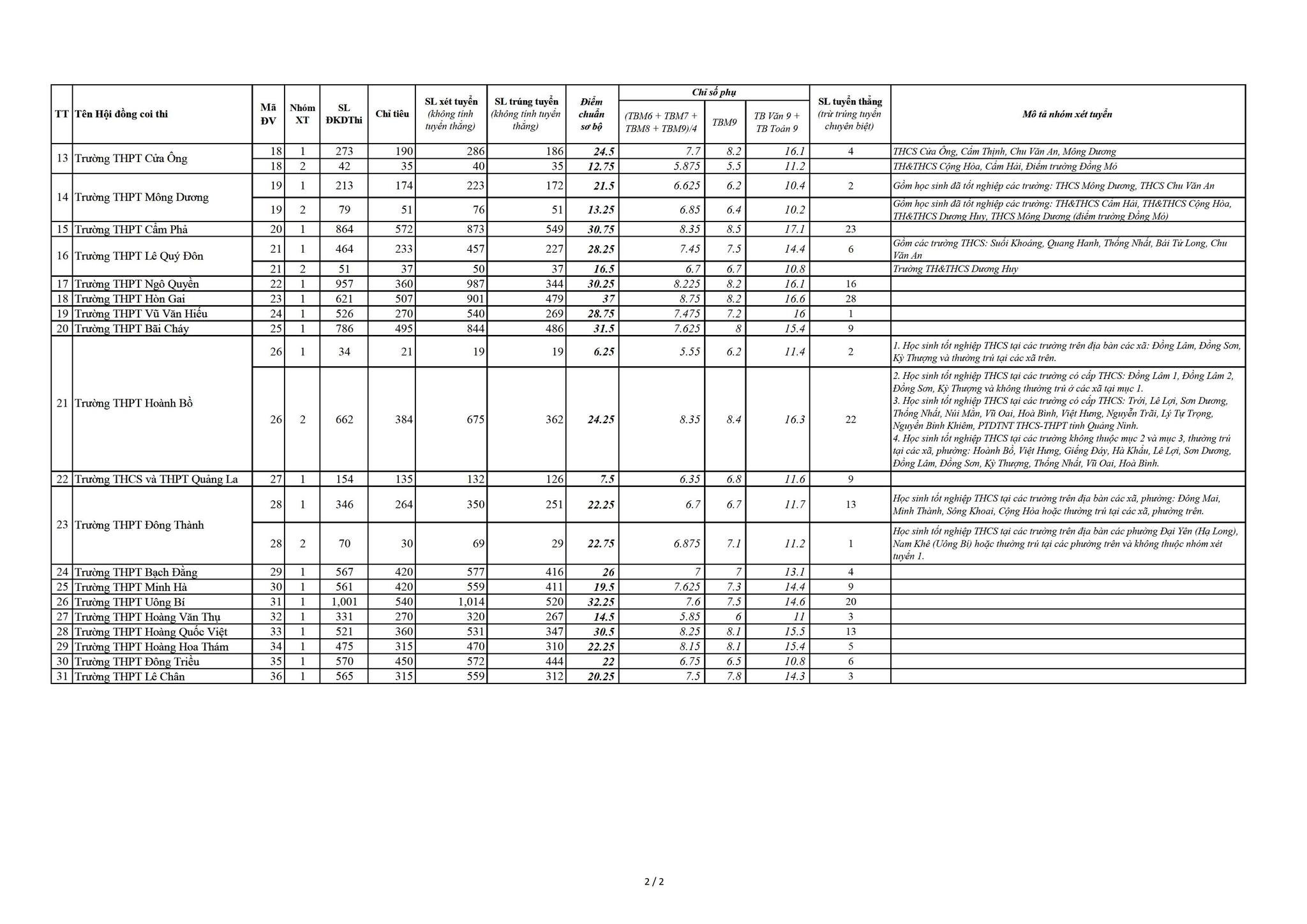 Điểm chuẩn trường THPT Hòn Gai năm 2024 – 2025
Điểm chuẩn trường THPT Hòn Gai năm 2024 – 2025

 Cuốn sách Vừa Lười Vừa Bạn Văn Giỏi Tiếng Anh
Cuốn sách Vừa Lười Vừa Bạn Văn Giỏi Tiếng Anh Bộ tài liệu chuẩn giúp bạn học từ vựng hữu ích cho giao tiếp
Bộ tài liệu chuẩn giúp bạn học từ vựng hữu ích cho giao tiếp
 Bộ sách công phá các môn học 10 cần thiết trong hành trang kiến thức của học sinh
Bộ sách công phá các môn học 10 cần thiết trong hành trang kiến thức của học sinh Bộ sách đột phá tư duy bồi dưỡng học sinh giỏi 10
Bộ sách đột phá tư duy bồi dưỡng học sinh giỏi 10 Bộ sách tự học tham khảo lớp 10 hữu ích cho các em
Bộ sách tự học tham khảo lớp 10 hữu ích cho các em