Khi bước vào học kỳ 2 lớp 7, các em sẽ đối mặt với khái niệm đại lượng tỉ lệ thuận – một phần kiến thức nền tảng và cần thiết trong toán học. Khái niệm này không chỉ xuất hiện trong sách vở mà còn thường xuyên xuất hiện trong kỳ thi. Vì vậy, việc ôn tập thật kỹ sẽ giúp các em đạt điểm cao trong các bài kiểm tra. Dưới đây là lý thuyết, các dạng bài tập liên quan và ví dụ cụ thể để các em tham khảo và củng cố kiến thức.
I. Lý thuyết về đại lượng tỉ lệ thuận lớp 7
1. Định nghĩa
Nếu đại lượng y liên hệ với đại lượng x theo công thức y = ax (a là hàng số khác 0) thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ a.
Nếu y tỉ lệ thuận với x theo hệ số tỉ lệ a (a ≠ 0) thì x tỉ lệ thuận với y theo hệ số tỉ lệ 1/a.
Khi đó ta nói x và y là hai đại lượng tỉ lệ thuận.
2. Tính chất
Nếu đại lượng y tỉ lệ thuận với đại lượng x thì:
Tỷ số hai giá trị tương ứng của chúng luôn không đổi (và bằng hệ số tỉ lệ):
y1/x1 = y2/x2 = y3/x3 = … = a.
Tỷ số hai giá trị bất kỳ của đại lượng này bằng tỷ số hai giá trị tương ứng của đại lượng kia:
y1/y2 = x1/x2, y1/y3 = x1/x3, y2/y3 = x2/x3,…
 Lý thuyết về đại lượng tỉ lệ thuận lớp 7
Lý thuyết về đại lượng tỉ lệ thuận lớp 7
II. Các dạng toán về đại lượng tỉ lệ thuận lớp 7
Dạng 1: Nhận biết hai đại lượng tỉ lệ thuận. Xác định hệ số tỉ lệ và công thức biểu diễn đại lượng tỉ lệ thuận
+ Phương pháp
Bước 1: Xác định hai đại lượng x, y và hệ số tỉ lệ k.
Bước 2: Sử dụng công thức y = kx để xác định quan hệ của hai đại lượng.
+ Các ví dụ
Ví dụ 1:
Xác định hai đại lượng trong các trường hợp dưới đây có phải hai đại lượng tỉ lệ thuận không? Nếu phải, viết công thức liên hệ và xác định hệ số tỉ lệ trong mỗi trường hợp:
a) Quãng đường ô tô đi được S (km) trong thời gian t (giờ), biết vận tốc của ô tô là 30km/h.
b) Diện tích S (m²) cánh đồng hình chữ nhật có hai kích thước là 3m và a (m).
c) Tổng số sản phẩm K ( sản phẩm) do công nhân làm được trong a ngày, biết mỗi ngày công nhân đó làm được 30 sản phẩm.
Hướng dẫn giải
a) Quãng đường đi được S (km) trong thời gian t (giờ) là hai đại lượng tỉ lệ thuận.
Công thức liên hệ: S = 30t (km). Hệ số tỉ lệ k = 30.
b) Diện tích S (m²) cánh đồng hình chữ nhật và độ dài một cạnh a (m) là hai đại lượng tỉ lệ thuận.
Công thức liên hệ: S = 3a (m²). Hệ số tỉ lệ k = 3.
c) Tổng số sản phẩm K (sản phẩm) do công nhân làm được trong a ngày là hai đại lượng tỉ lệ thuận.
Công thức liên hệ: K = 30a (sản phẩm). Hệ số tỉ lệ k = 30.
Ví dụ 2:
Cho hai đại lượng x, y tỉ lệ thuận với nhau. Biết đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5. Hỏi đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ bao nhiêu?
Hướng dẫn giải
Vì đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 5 nên y = 5x => x = (1/5)y.
Suy ra đại lượng x tỉ lệ thuận với đại lượng y theo hệ số tỉ lệ 1/5.
Dạng 2: Tìm các đại lượng dựa vào tính chất tỉ lệ thuận
+ Phương pháp
Thực hiện theo các bước sau:
Bước 1: Sử dụng tính chất của hai đại lượng tỉ lệ thuận để xác định mối liên hệ giữa các đại lượng.
Bước 2: Sử dụng tính chất của dãy tỉ lệ bằng nhau để tìm các đại lượng.
+ Các ví dụ
Ví dụ 1:
Cho x và y là hai đại lượng tỉ lệ thuận. Gọi x1, x2 là hai giá trị của x và y1, y2 là hai giá trị tương ứng của y. Biết rằng khi x1 = 2, x2 = 6 thì 2y1 – 3y2 = – 28.
a) Tính y1 và y2.
b) Xác định công thức liên hệ của y và x.
Hướng dẫn giải
a) Vì x và y là hai đại lượng tỉ lệ thuận nên áp dụng tính chất của hai đại lượng tỉ lệ thuận, ta có y1/x1 = y2/x2 = k.
Áp dụng tính chất của dãy tỉ lệ bằng nhau, ta có:
k = y1/x1 = y2/x2 => (2y1 – 3y2)/(2 – 6) = –28 => k = 2.
Suy ra y1 = 2×1 = 2(2) = 4, y2 = 2×2 = 2(6) = 12.
Vậy y1 = 4, y2 = 12.
b) Công thức liên hệ của y và x là y = 2x.
Ví dụ 2:
Cho x, y là hai đại lượng tỉ lệ thuận. Biết rằng với hai giá trị x1, x2 của x thỏa mãn điều kiện 3×1 – 4×2 = 42,5 thì hai giá trị tương ứng y1, y2 của y thỏa mãn điều kiện 3y1 – 4y2 = -8,5.
a) Tìm hệ số tỉ lệ của y đối với x.
b) Biết x1, x2 tỉ lệ với 5 và 4. Tính x1, x2, y1, y2.
Hướng dẫn giải
a) Vì x và y là hai đại lượng tỉ lệ thuận nên áp dụng tính chất của hai đại lượng tỉ lệ thuận, ta có:
y1/x1 = y2/x2 = k.
Áp dụng tính chất của dãy tỉ lệ bằng nhau, ta có:
k = y1/x1 = y2/x2; k = 3y1/3×1 = 4y2/4×2 = (3y1 – 4y2)/(3×1 – 4×2) = (-8,5)/42,5 = – 1/5.
Vậy đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ k = – 1/5.
b) Vì x1, x2 tỉ lệ với 5 và 4 nên:
x1/5 = x2/4 = 3×1/15 = 4×2/16 = (3×1 – 4×2)/(15 – 16) = 42,5/(-1) = – 42,5.
Suy ra x1 = 5 (–42,5) = –212,5; x2 = 4 (–42,5) = –170.
Ta có y1 = (-1/5)x1 = –1/5 (–212,5) = 42,5 và y2 = (-1/5)x2 = (-1/5) (–170) = 34.
Vậy x1 = –212,5; x2 = –170; y1 = 42,5; y2 = 34.
Dạng 3: Lập bảng giá trị tương ứng của hai đại lượng tỉ lệ thuận
+ Phương pháp
Thực hiện theo các bước sau:
Bước 1: Xác định hệ số tỉ lệ k.
Bước 2: Sử dụng công thức y = k để tìm các giá trị tương ứng của x và y.
+ Các ví dụ
Ví dụ 1:
Cho biết x và y là hai đại lượng tỉ lệ thuận và bảng sau:
| x |
-8 |
-6 |
-2 |
4 |
4√2 |
16 |
| y |
1 |
8 |
a) Xác định hệ số tỉ lệ của y đối với x.
b) Điền số thích hợp vào ô trống trong bảng.
Hướng dẫn giải
a) Vì x, y là hai đại lượng tỉ lệ thuận nên y = kx.
Thay x = 16 và y = 8, ta có: 8 = k * 16 => k = 1/2.
Vậy hệ số tỉ lệ của y đối với x là k = 1/2.
b) Kết quả điền vào ô trống như sau:
| x |
-8 |
-6 |
-2 |
4 |
4√2 |
16 |
| y |
-4 |
-3 |
-1 |
1 |
2√2 |
8 |
Ví dụ 2:
Cho biết x và y là hai đại lượng tỉ lệ thuận. Khi hai giá trị x1, x2 của x có điều kiện 3×1 – 4×2 = 42,5, thì hai giá trị tương ứng y1, y2 của y có điều kiện 3y1 – 4y2 = -8,5.
a) Hãy biểu diễn đại lượng y theo đại lượng x. Viết công thức liên hệ giữa x và y.
b) Hoàn thành bảng sau:
| x |
-3 |
-1 |
1/2 |
2 |
4 |
5 |
| y |
-4 |
-5/3 |
9 |
Hướng dẫn giải
a) Vì x, y là hai đại lượng tỉ lệ thuận nên y = kx.
Áp dụng tính chất hai đại lượng tỉ lệ thuận, ta có:
y1/x1 = y2/x2 = k.
Áp dụng tính chất của dãy tỉ lệ bằng nhau, ta có:
k = y1/x1 = y2/x2 = ((y1 – y2)/(x1 – x2) = 5/(-2) = -5/2.
Vậy y = (-5/2)x.
b) Kết quả điền vào ô trống như sau:
| x |
8/5 |
2/3 |
-3 |
-1 |
1/2 |
2 |
4 |
5 |
-18/5 |
| y |
-4 |
-5/3 |
-15/2 |
5/2 |
-5/4 |
-5 |
-10 |
-25/2 |
9 |
Dạng 4: Một số bài toán có lời văn về đại lượng tỉ lệ thuận
+ Phương pháp
Thực hiện theo các bước sau:
Bước 1: Xác định tương quan giữa hai đại lượng tỉ lệ thuận.
Bước 2: Áp dụng tính chất và tỷ lệ các giá trị của hai đại lượng tỉ lệ thuận để suy ra giá trị cần tìm.
+ Các ví dụ
Ví dụ 1:
Cho biết 1 tấn nước biển chứa 24kg muối.
a) Giả sử x tấn nước biển chứa y(kg) muối. Hãy biểu diễn y theo x.
b) Hỏi trong 2,5 tấn nước biển chứa bao nhiêu gam muối?
Hướng dẫn giải
a) Vì khối lượng muối có trong nước biển và khối lượng nước biển là hai đại lượng tỉ lệ thuận nên y/(x * 1000) = 24/1000 => y = 24x (kg).
b) Trong 2,5 tấn nước biển chứa số kg muối là 24 * 2,5 = 60 (kg).
Vậy trong 2,5 tấn nước biển chứa số gam muối là 60 * 1000 = 60000 (gam).
Ví dụ 2:
Biết 15 công nhân cùng làm trong một khoảng thời gian thì được 300 sản phẩm. Hỏi 20 công nhân làm trong cùng khoảng thời gian như vậy thì được bao nhiêu sản phẩm? (Năng suất của mỗi công nhân là giống nhau).
Hướng dẫn giải
Gọi số sản phẩm 20 công nhân làm được trong thời gian đã cho là x (sản phẩm).
Vì số công nhân và số sản phẩm là hai đại lượng tỉ lệ thuận nên 20/15 = x/300 => x = (20*300)/15 = 400 (sản phẩm).
Vậy 20 công nhân làm trong cùng khoảng thời gian như vậy thì được 400 sản phẩm.
III. Bài tập về đại lượng tỉ lệ thuận lớp 7
Dưới đây là một số bài toán về đại lượng tỉ lệ thuận lớp 7 để các em tham khảo:
 Bài tập về đại lượng tỉ lệ thuận lớp 7
Bài tập về đại lượng tỉ lệ thuận lớp 7
Trên đây là lý thuyết và các dạng bài tập về đại lượng tỉ lệ thuận lớp 7 kèm lời giải chi tiết để các em tham khảo. Hy vọng chúng sẽ giúp các em đạt điểm cao trong các bài kiểm tra và bài thi môn Toán.
Để ôn tập thêm kiến thức Toán lớp 7 tập 2, các em nên tham khảo thêm cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 7 Tập 2 của Tkbooks nhé!
Link để tham khảo sách: https://drive.google.com/file/d/1R-JkEKNI4j0d-bIDytNA-0KmRrQa5UZP/view
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh hàng đầu tại Việt Nam!
Tkbooks.vn
 Nối chữ với hình tương ứng
Nối chữ với hình tương ứng Nối chữ với hình tương ứng
Nối chữ với hình tương ứng
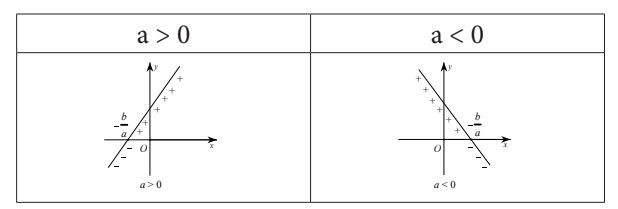 Minh họa bằng đồ thị dấu của nhị thức bậc nhất
Minh họa bằng đồ thị dấu của nhị thức bậc nhất Ví dụ về bất phương trình chứa ẩn ở mẫu
Ví dụ về bất phương trình chứa ẩn ở mẫu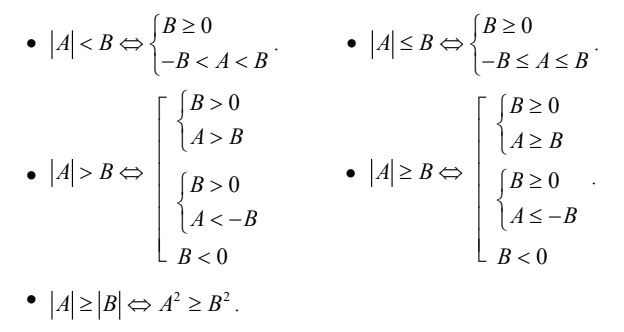 Bất phương trình chứa dấu giá trị tuyệt đối
Bất phương trình chứa dấu giá trị tuyệt đối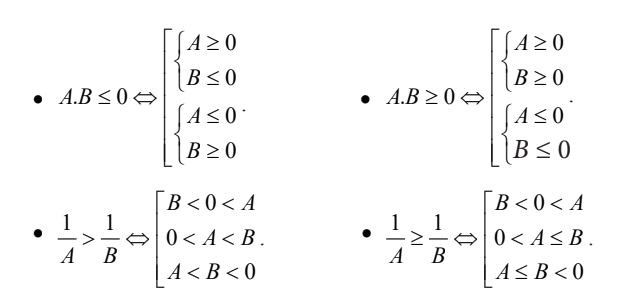 Các bất phương trình khác
Các bất phương trình khác Ví dụ về bất phương trình bậc nhất hai ẩn
Ví dụ về bất phương trình bậc nhất hai ẩn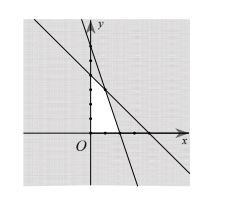 Đồ thị miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
Đồ thị miền nghiệm của hệ bất phương trình bậc nhất hai ẩn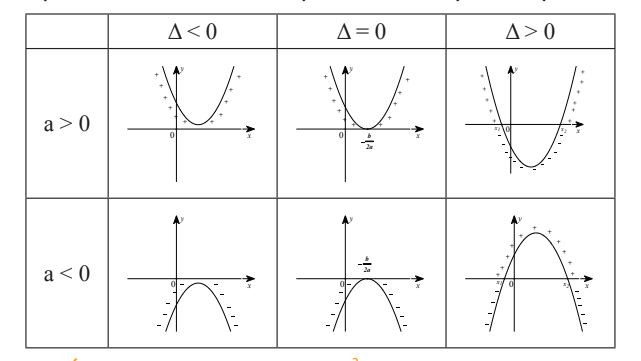 Minh họa hình học về dấu của tam thức bậc 2
Minh họa hình học về dấu của tam thức bậc 2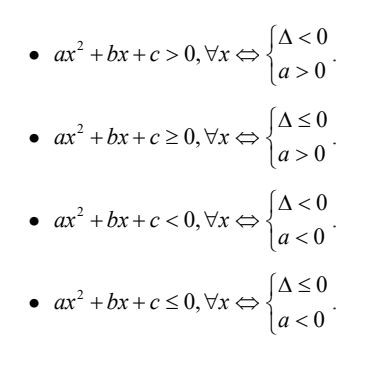 Điều kiện tương đương của bất phương trình bậc 2 một ẩn
Điều kiện tương đương của bất phương trình bậc 2 một ẩn Bài tập bất đẳng thức và bất phương trình
Bài tập bất đẳng thức và bất phương trình Bài tập bất đẳng thức và bất phương trình (tiếp theo)
Bài tập bất đẳng thức và bất phương trình (tiếp theo)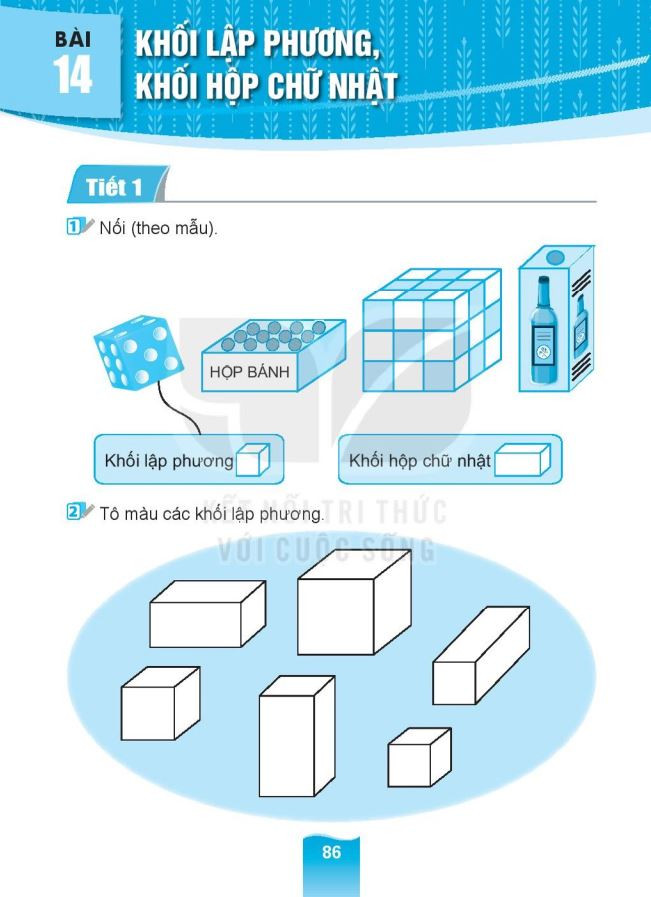
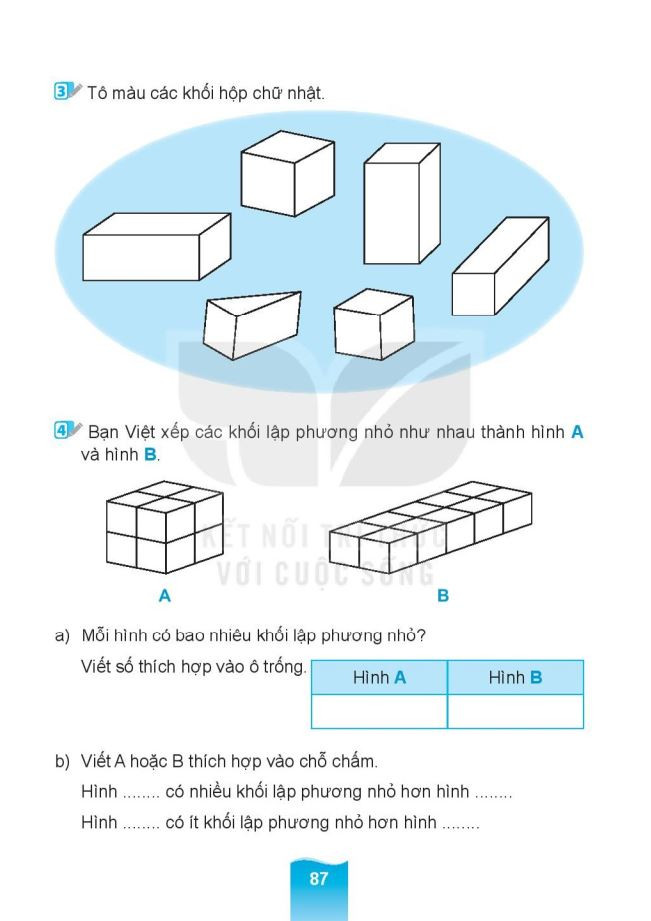 Bài Tập Đếm Khối Lập Phương Lớp 1 – File 1
Bài Tập Đếm Khối Lập Phương Lớp 1 – File 1 Bài Tập Đếm Khối Lập Phương Lớp 1 – File 2
Bài Tập Đếm Khối Lập Phương Lớp 1 – File 2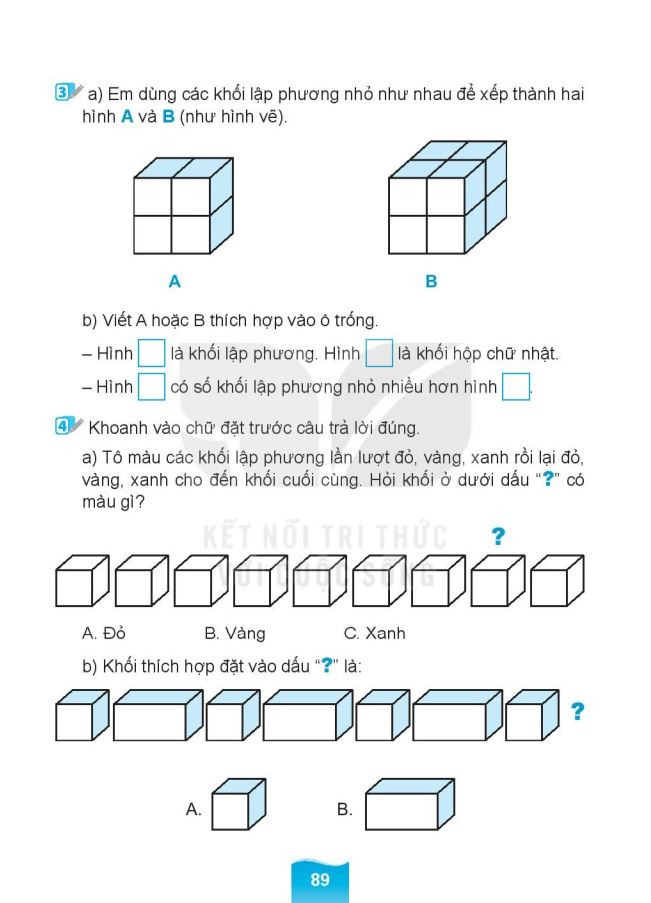 Bài Tập Đếm Khối Lập Phương Lớp 1 – File 3
Bài Tập Đếm Khối Lập Phương Lớp 1 – File 3 Giúp trẻ nhận biết khối lập phương qua đồ chơi hoặc các đồ vật trong nhà
Giúp trẻ nhận biết khối lập phương qua đồ chơi hoặc các đồ vật trong nhà
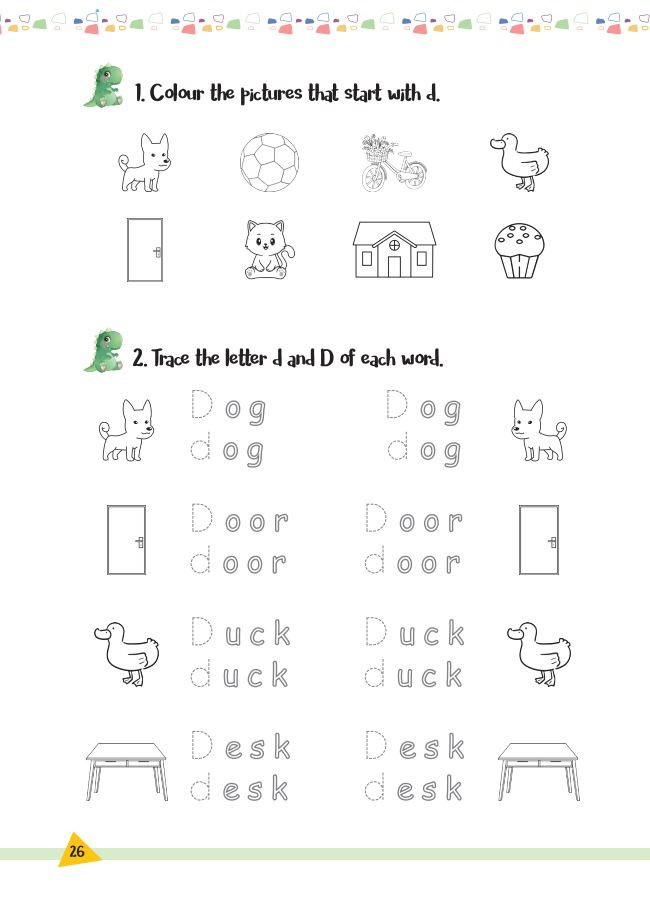
 Bài tập Unit 4 – File 2
Bài tập Unit 4 – File 2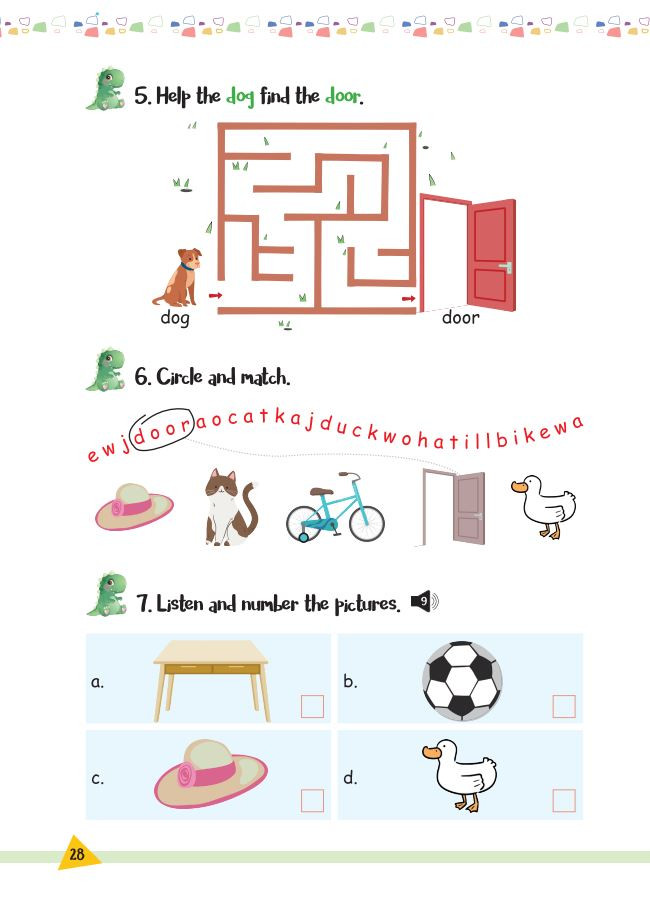 Bài tập Unit 4 – File 3
Bài tập Unit 4 – File 3 Bài tập Unit 4 – File 4
Bài tập Unit 4 – File 4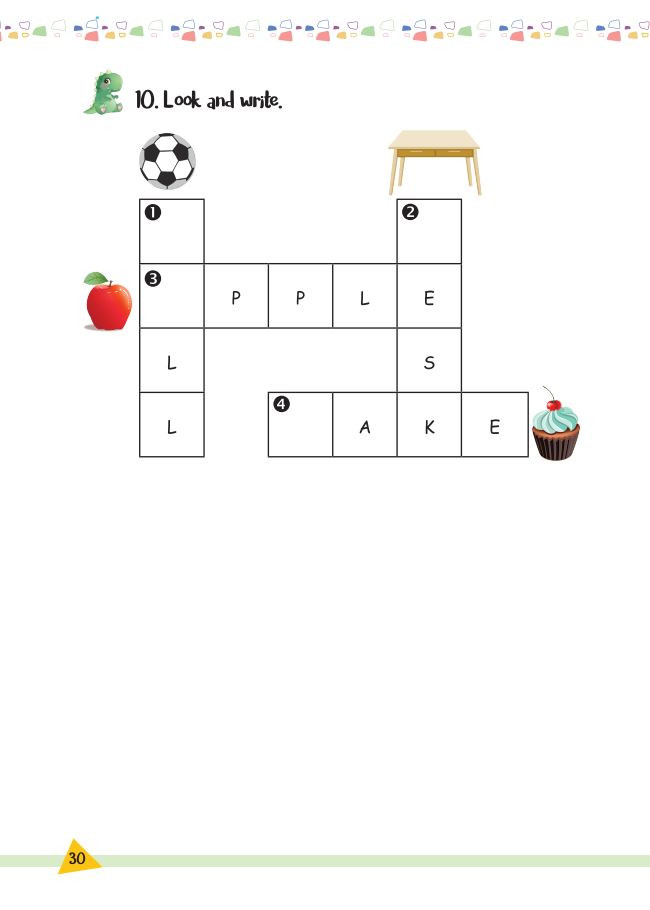 Bài tập Unit 4 – File 5
Bài tập Unit 4 – File 5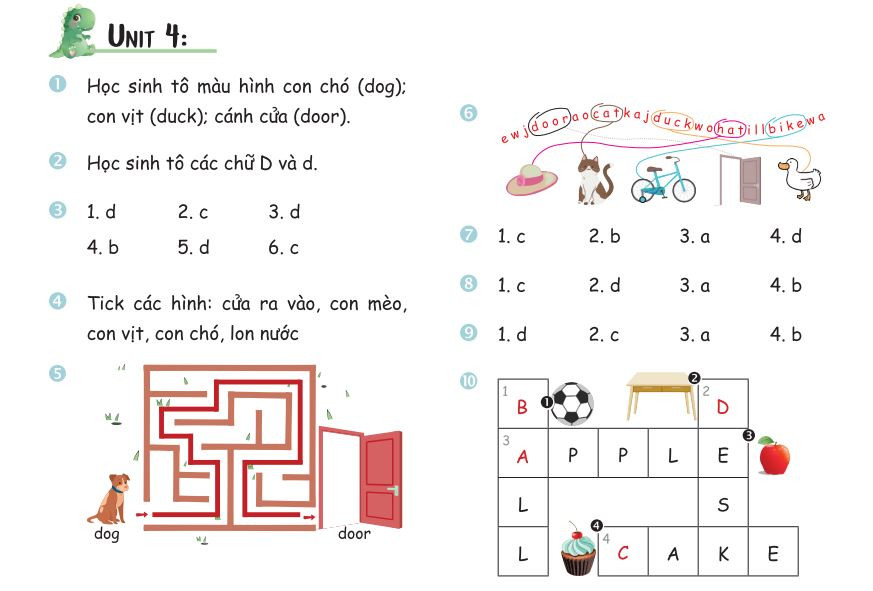 Phần đáp án
Phần đáp án
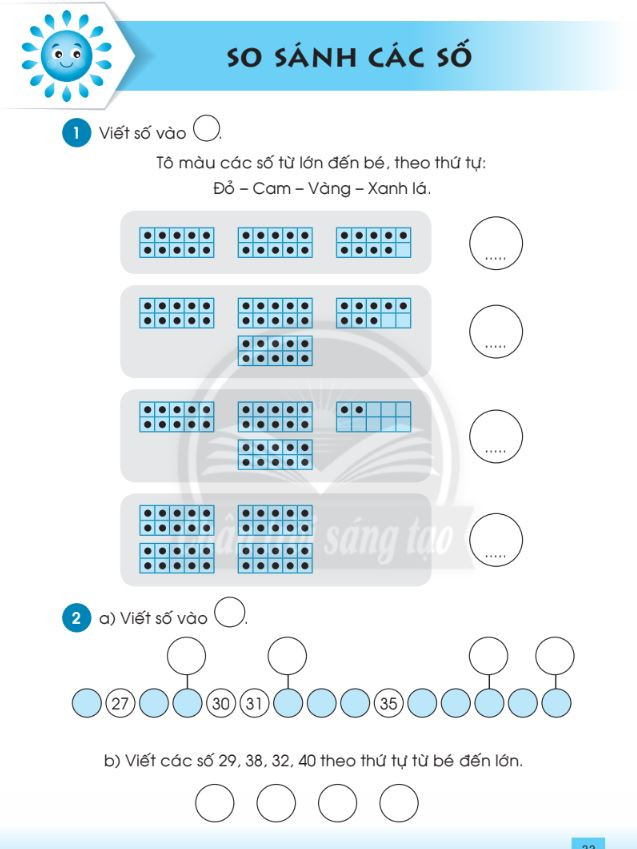
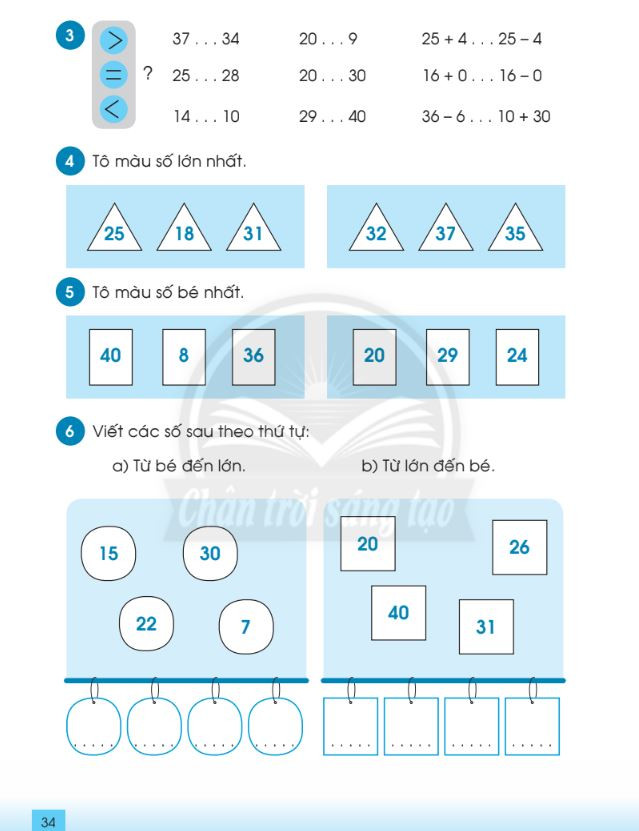 Bài tập so sánh số có hai chữ số – File 2
Bài tập so sánh số có hai chữ số – File 2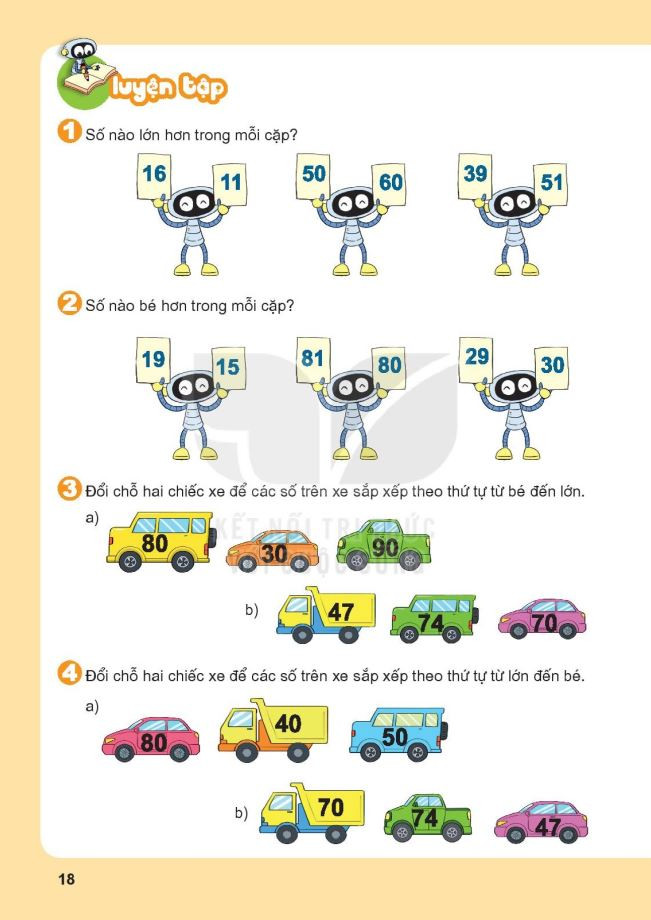 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 1
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 1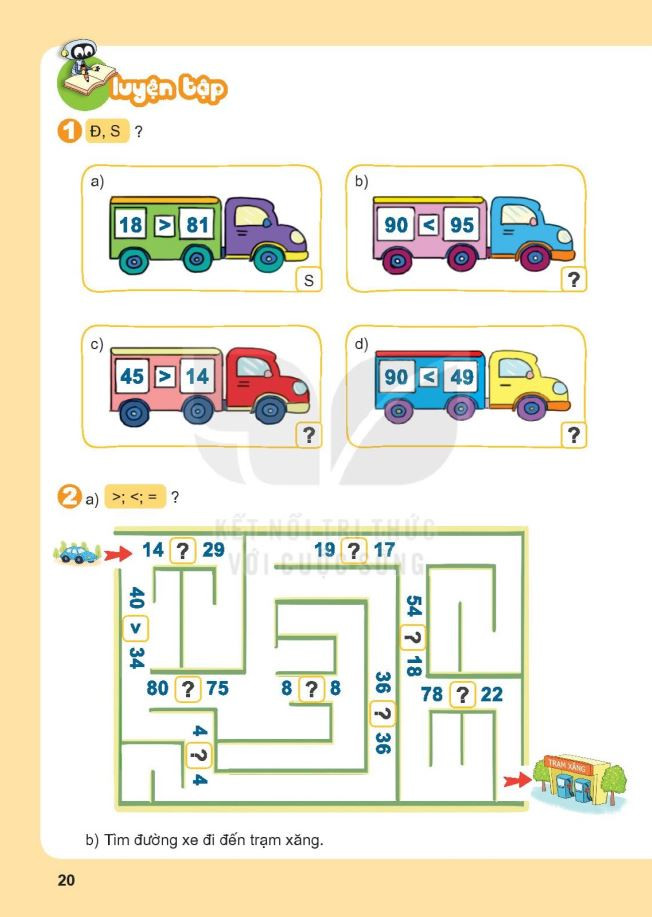 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 2
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 2 Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 3
Bài tập luyện tập chung so sánh số có hai chữ số lớp 1 – File 3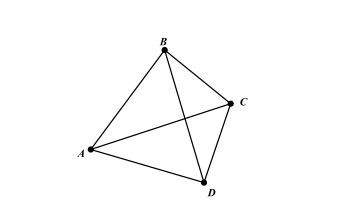
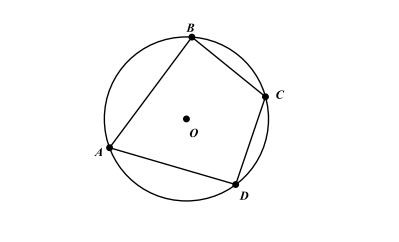 Ví dụ về tứ giác nội tiếp
Ví dụ về tứ giác nội tiếp Hình vẽ minh họa bài 2
Hình vẽ minh họa bài 2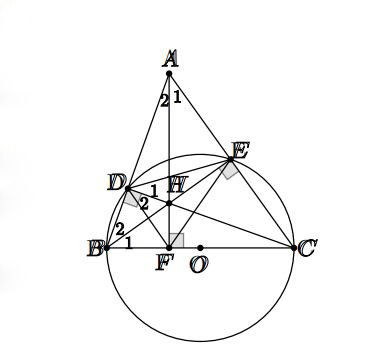 Hình vẽ minh họa bài 3
Hình vẽ minh họa bài 3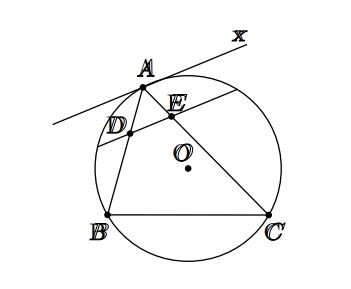 Hình vẽ minh họa bài 4
Hình vẽ minh họa bài 4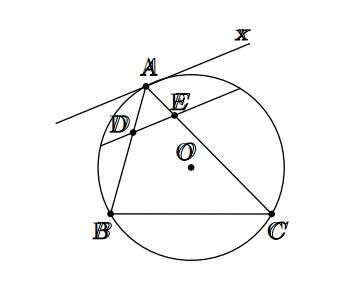 Hình vẽ minh họa bài 5
Hình vẽ minh họa bài 5
 Bài tập về đại lượng tỉ lệ thuận lớp 7
Bài tập về đại lượng tỉ lệ thuận lớp 7