Hàm số bậc 2 là một trong những kiến thức quan trọng trong chương trình Toán học lớp 10. Phần kiến thức này thường xuyên xuất hiện trong các bài thi Toán THPT, vì vậy, việc nắm vững và củng cố lý thuyết về hàm số bậc 2 là vô cùng cần thiết cho các bạn học sinh.
Dưới đây là tổng hợp lý thuyết, bài tập và hướng dẫn giải chi tiết về hàm số bậc 2. Các em hãy ghi nhớ và ôn tập nhiều lần để có thể nắm chắc kiến thức nhé!
1. Hàm Số Bậc 2 Là Gì?
Hàm số bậc hai được biểu diễn bằng công thức (y = ax^2 + bx + c) (với (a neq 0)). Tập xác định của hàm số này là (D = R).
Hàm số (y = ax^2) (với (a neq 0)) đã được học ở lớp 9 là một trường hợp đặc biệt của hàm số này.
Ví dụ:
Dưới đây là một số ví dụ về hàm số bậc 2 để các em dễ hình dung:
VÍ dụ và bài tập về hàm số bậc 2
2. Đồ Thị Của Hàm Số Bậc Hai
Đồ thị của hàm số (y = ax^2 + bx + c) (với (a neq 0)) là một đường parabol có đỉnh là điểm (I(-frac{b}{2a}; -frac{Delta}{4a})), có trục đối xứng là đường thẳng (x = -frac{b}{2a}). Parabol này quay lên trên nếu (a > 0) và quay xuống dưới nếu (a < 0).
Cách Vẽ:
Để vẽ parabol (y = ax^2 + bx + c) (với (a neq 0), ta thực hiện các bước sau:
- B1: Xác định tọa độ của đỉnh (I(-frac{b}{2a}; -frac{Delta}{4a})).
- B2: Vẽ trục đối xứng (x = -frac{b}{2a}).
- B3: Xác định tọa độ các giao điểm của parabol với trục tung (điểm ((0;c))) và trục hoành (nếu có).
- B4: Vẽ parabol.
Khi vẽ parabol cần chú ý đến dấu của hệ số (a) ( (a > 0) parabol quay lên trên, (a < 0) parabol quay xuống dưới).
Đồ thị của hàm số bậc 2 là một parabol
3. Chiều Biến Thiên Của Hàm Số Bậc Hai
Dựa vào đồ thị hàm số (y = ax^2 + bx + c) (với (a neq 0)), ta có bảng biến thiên của nó trong hai trường hợp (a > 0) và (a < 0).
Từ đó, ta có định lý dưới đây:
- Nếu (a > 0) thì hàm số (y = ax^2 + bx + c nghịch biến trên khoảng ((-∞; -frac{b}{2a})); đồng biến trên khoảng ((- frac{b}{2a}; + ∞)); -frac{Delta}{4a}) là giá trị nhỏ nhất của hàm số.
- Nếu (a < 0) thì hàm số (y = ax^2 + bx + c) đồng biến trên khoảng ((-∞; -frac{b}{2a})); nghịch biến trên khoảng ((- frac{b}{2a}; + ∞)); -frac{Delta}{4a}) là giá trị lớn nhất của hàm số.
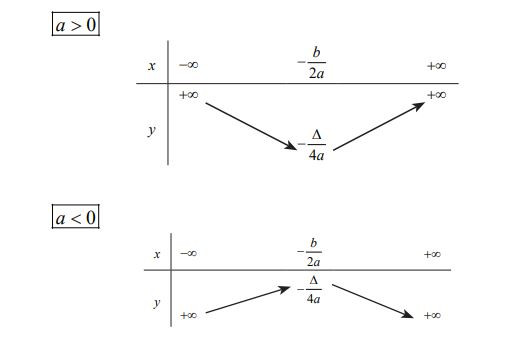Chiều biến thiên của hàm số bậc 2
Ví dụ:
Bài tập ví dụ về tính đồng biến và nghịch biến của hàm số bậc 2
4. Một Số Mô Hình Toán Học Sử Dụng Hàm Số Bậc Hai
Hàm số bậc hai được sử dụng trong nhiều mô hình thực tế. Dưới đây ta xét một số mô hình đơn giản thường gặp.
Phương trình chuyển động của vật chuyển động thẳng biến đổi đều
[X = X_0 + V_0t + frac{(at^2)}{2}]
Trong đó (X_0) là tọa độ ban đầu của vật, (V_0) là vận tốc ban đầu của vật và (a) là gia tốc của vật (a cùng dấu với V0 nếu vật chuyển động nhanh dần đều và ngược dấu với V0 nếu vật chuyển động chậm dần đều). Như vậy tọa độ (x(t)) của vật là một hàm số bậc hai của thời gian (t).
Nói riêng, khi bỏ qua sức cản của không khí, nếu ném một vật lên trên theo phương thẳng đứng thì chuyển động của vật sẽ chỉ chịu ảnh hưởng của trọng lực và vật sẽ có gia tốc bằng gia tốc trọng trường (g = 9.8 m/s²).
Đặc biệt, khi bỏ qua sức cản không khí, nếu một vật rơi tự do từ độ cao (Y_0) (mét) so với mặt đất thì độ cao (Y(t)) của nó tại thời điểm t (giây) được cho bởi công thức:
[Y(t) = Y_0 – frac{(1/2)gt^2}{2}]
5. Doanh Thu Bán Hàng
Trong kinh tế, doanh thu bán hàng là số tiền nhận được khi bán một mặt hàng. Doanh thu (R) bằng đơn giá (x) của mặt hàng (tức là giá bán của một sản phẩm) nhân với số lượng (n) sản phẩm đã bán được, tức là
[R = x.n]
Định luật nhu cầu khẳng định rằng giá giữa (x) và (n) có mối liên hệ tỷ lệ nghịch với nhau; khi cái này tăng thì cái kia sẽ giảm. Phương trình liên hệ giữa (x) và (n) gọi là phương trình nhu cầu. Nếu phương trình nhu cầu là liên hệ bậc nhất, tức là (n = a – bx) (a, b là những hệ số dương), thì doanh thu bán hàng sẽ là hàm số bậc hai của đơn giá:
[R(x) = x.n = x(a – bx) = ax – bx^2]
Khi đó người ta thường quan tâm đến việc tìm giá bán (x) để doanh thu đạt cực đại, hoặc tìm giá bán (x) để doanh thu vượt một mức nào đó.
6. Các Bài Tập Luyện Tập Về Hàm Số Bậc 2
Các em hãy làm bài tập luyện tập về hàm số bậc 2 để nắm chắc lý thuyết về phần này hơn.
Đồ thị của hàm số bậc 2 là một parabol
Kiến thức về hàm số bậc 2 được trình bày rất chi tiết và dễ hiểu trong cuốn sách Sổ tay Toán học cấp 3 All in one. Các em hãy mua ngay cuốn sách này để nắm trọn kiến thức môn Toán trong chương trình THPT nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh THPT hàng đầu tại Việt Nam.
Tkbooks.vn
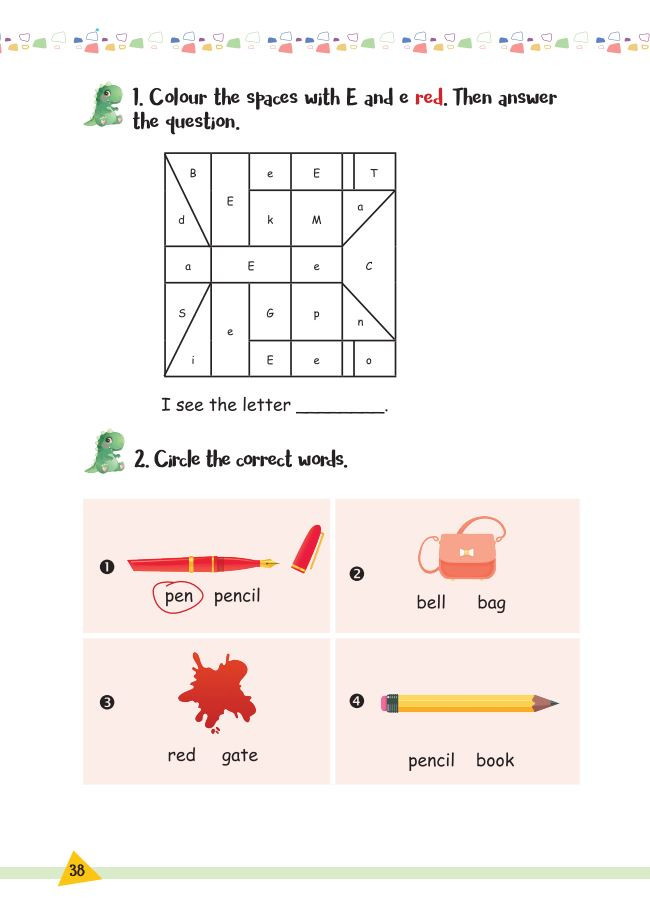
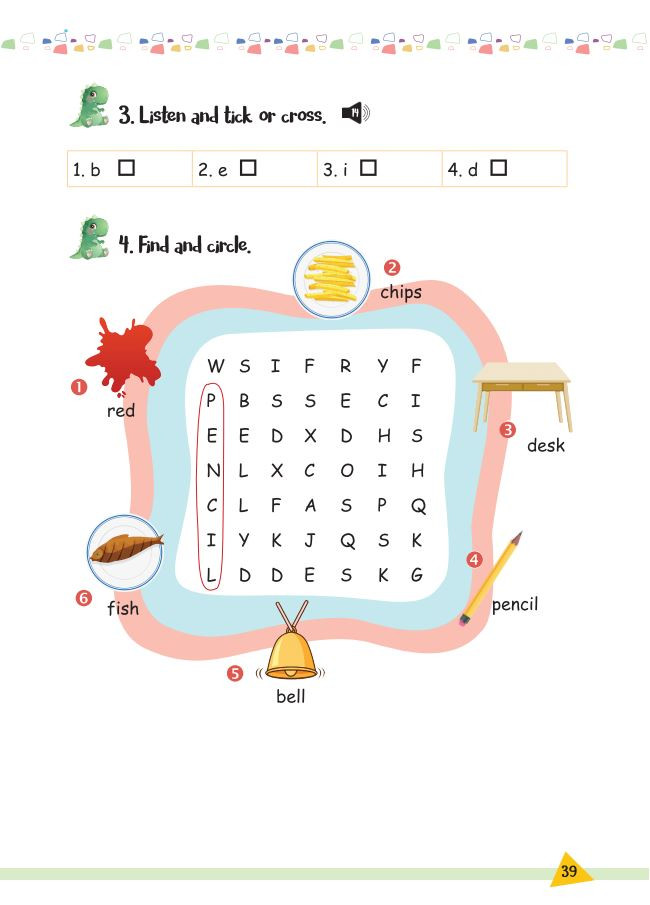Bài tập Unit 6 – File 2
Bài tập Unit 6 – File 3
Bài tập Unit 6 – File 4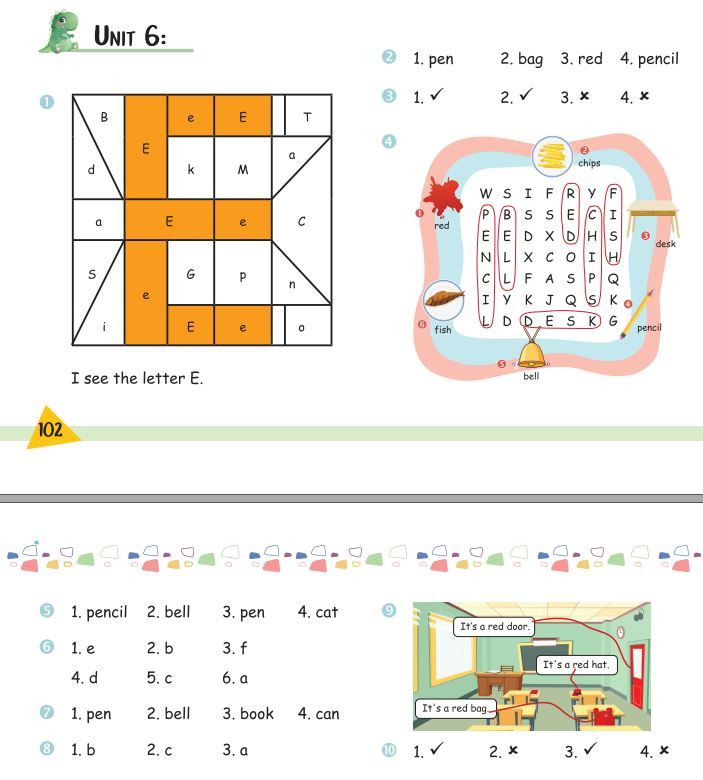
Phần đáp án bài tập Unit 6
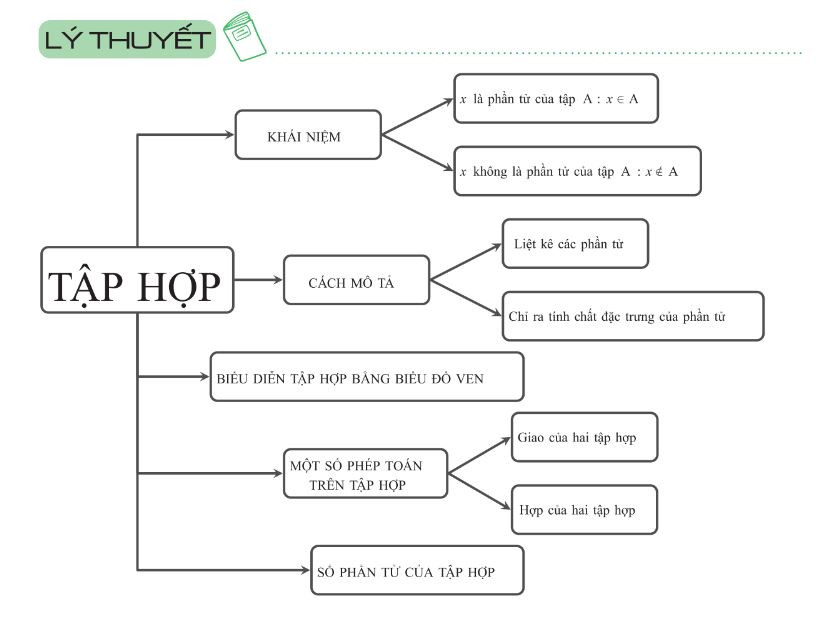
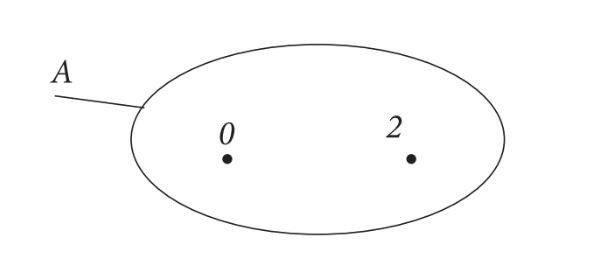Minh họa một tập hợp cho trước bằng hình vẽ – Ảnh 2
Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung Việc học sách tham khảo giúp bạn rèn luyện được sự tập trung
Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài Sách tham khảo tạo khả năng tư duy logic và ghi nhớ lâu dài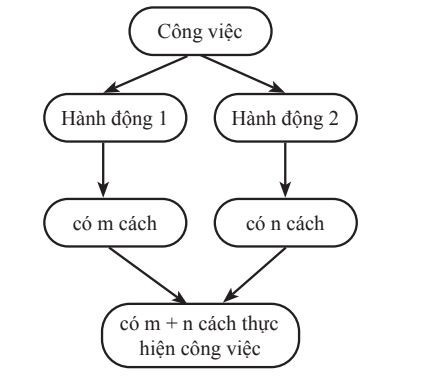
Ví dụ về quy tắc cộng
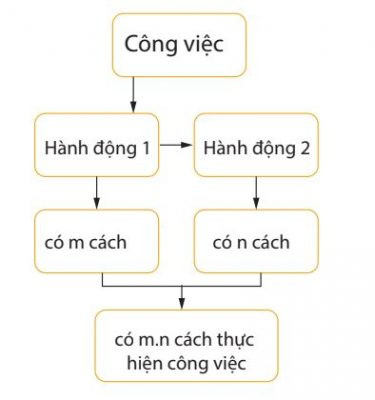Quy tắc nhân
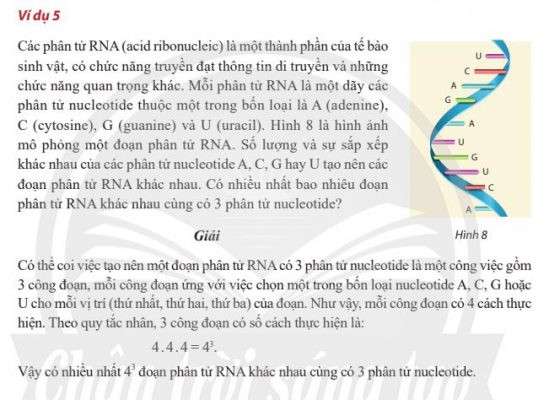Ví dụ về quy tắc nhân
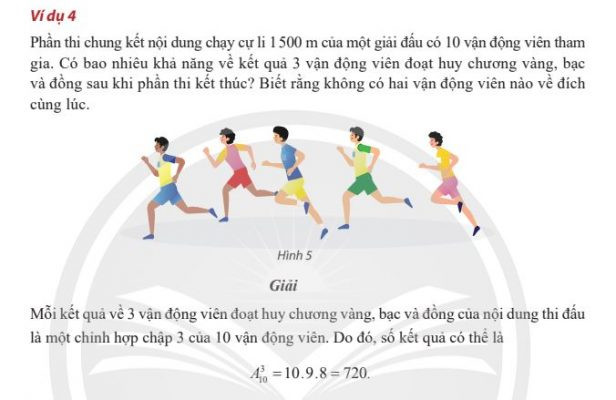Ví dụ về chỉnh hợp
Ví dụ về tổ hợp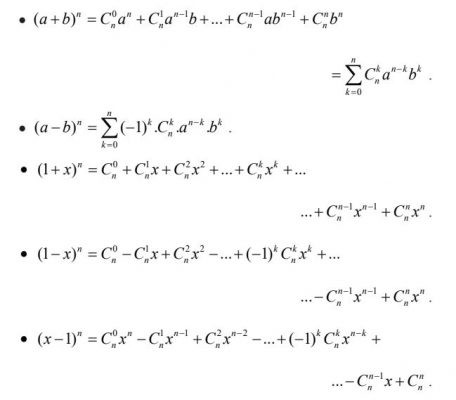
Nhị thức Newton
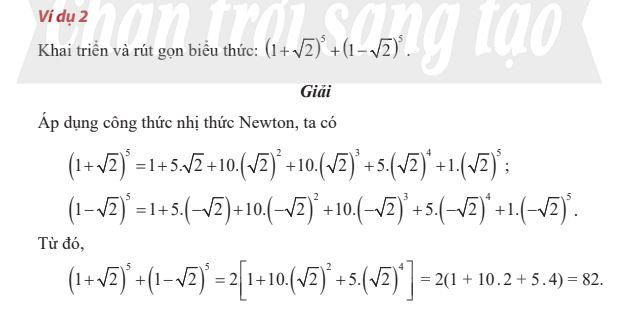Ví dụ về nhị thức Newton
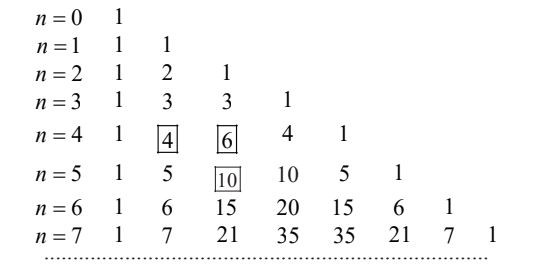Tam giác Pascal
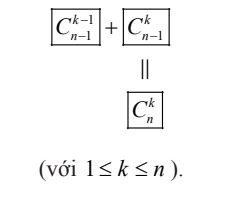Hàng dọc thức Pascal
Cách tính tổ hợp bằng máy tính cầm tay
Bài tập về tổ hợp, chỉnh hợp
Bài tập về nhị thức Newton
Cuốn sách Đề Ôn Tập Từ Vựng Và Cấu Trúc Tiếng Anh Lớp 2
Cuốn sách Super Test – Đề Kiểm Tra Nhanh Tiếng Anh Lớp 2
