Hệ tọa độ trong không gian là một phần kiến thức quan trọng trong chương trình Toán học THPT. Kiến thức này thường được sử dụng trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì vậy việc nắm vững phần này là rất cần thiết để các em có thể đạt được điểm số cao.
Dưới đây, chúng tôi sẽ tổng hợp lại những kiến thức cơ bản về Hệ tọa độ trong không gian. Các em hãy lưu ý và ôn tập thường xuyên để nắm vững kiến thức nhé!
I. Định nghĩa Hệ tọa độ trong không gian
1. Định nghĩa
Hệ tọa độ trong không gian được định nghĩa như sau:
[ vec{u} = (x; y; z) ]
[ vec{u} = x.vec{i} + y.vec{j} + z.vec{k} ]
Trong đó, (vec{i}, vec{j}, vec{k}) là các vectơ đơn vị tương ứng trên các trục tọa độ (Ox, Oy, Oz).
Hệ tọa độ trong không gian
2. Tính chất
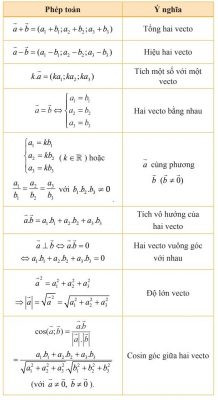
Cho hai vectơ ( vec{a} = (a_1; a_2; a_3) ) và ( vec{b} = (b_1; b_2; b_3) ), với (k) là số thực tùy ý, ta có:
[
vec{AB} = (b_1 – a_1; b_2 – a_2; b_3 – a_3)
]
[
|vec{AB}| = sqrt{(b_1 – a_1)^2 + (b_2 – a_2)^2 + (b_3 – a_3)^2}
]
II. Định nghĩa Địa điểm
1. Định nghĩa
Địa điểm M(x,y,z) được xác định từ điểm O như sau:
[ M(x;y;z) ]
Trong đó:
- (x): hoành độ,
- (y): tung độ,
- (z): cao độ.
Chú ý: Trong hệ tọa độ Oxyz, cho điểm M(x;y;z), ta có các khẳng định sau:
| Khẳng định | Mô tả |
|---|---|
| M ≡ O | (M(0;0;0)) |
| M ∈ (Oxy) | (z = 0) tương đương với (M(x;y;0)) |
| M ∈ (Oyz) | (x=0) tương đương với (M(0;y;z)) |
| M ∈ (Oxz) | (y=0) tương đương với (M(x;0;z)) |
| M ∈ Ox | (y = z = 0) tương đương với (M(x;0;0)) |
| M ∈ Oy | (x = z = 0) tương đương với (M(0;y;0)) |
| M ∈ Oz | (x = y = 0) tương đương với (M(0;0;z)) |
2. Tính chất
Cho bốn điểm không đồng phẳng (A(x_A; y_A; z_A), B(x_B; y_B; z_B), C(x_C; y_C; z_C), D(x_D; y_D; z_D)).
Tọa độ trung điểm I của đoạn thẳng AB là:
[ I = left(frac{x_A + x_B}{2}; frac{y_A + y_B}{2}; frac{z_A + z_B}{2}right) ]
Tọa độ trọng tâm G của tam giác ABC là:
[ G = left(frac{x_A + x_B + x_C}{3}; frac{y_A + y_B + y_C}{3}; frac{z_A + z_B + z_C}{3}right) ]
III. Tích có hướng của hai vectơ
1. Định nghĩa
Trong không gian Oxyz, cho hai vectơ:
[ vec{a} = (a_1; a_2; a_3) quad vec{b} = (b_1; b_2; b_3) ]
Tích có hướng của hai vectơ ( vec{a} ) và ( vec{b} ) được ký hiệu là ([vec{a}, vec{b}]) và được xác định như sau:
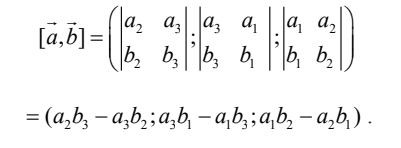Tích có hướng của hai vectơ
2. Tính chất
- (vec{a}) cùng phương với (vec{b}) khi và chỉ khi ([vec{a},vec{b}] = 0).
- ([vec{a},vec{b}]) vuông góc với cả hai vectơ (vec{a}) và (vec{b}).
- ([vec{b}, vec{a}] = -[vec{a},vec{b}]).
- ([vec{a},vec{b}] = |vec{a}| cdot |vec{b}| cdot sin(vec{a},vec{b}))
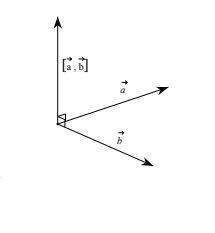Tính chất tích có hướng của hai vectơ
3. Ứng dụng
Xét sự đồng phẳng của ba vectơ:
- Ba vectơ (vec{a}; vec{b}; vec{c}) đồng phẳng nếu ([vec{a},vec{b}].vec{c} = 0).
- Bốn điểm (A, B,C,D) tạo thành tứ diện nếu ([vec{AB},vec{AC}].vec{AD} neq 0).
| Diện tích hình bình hành | (S{ABCD} = |left[vec{AB},vec{AD}right]|) |
|—|—|
| Tính diện tích tam giác | (S{ABC} = frac{1}{2}|left[vec{AB},vec{AC}right]|) |
| Tính thể tích hình hộp | (V{ABCD.A’B’C’D’} = [vec{AB},vec{AC}].vec{AD}) |
| Tính thể tích tứ diện | (V{ABCD} = frac{1}{6}[vec{AB},vec{AC}].vec{AD}) |
IV. Phương trình mặt cầu
1. Định nghĩa phương trình mặt cầu
Mặt cầu có tâm (I(a;b;c)) và bán kính (R) có phương trình:
[
(S): (x – a)^2 + (y – b)^2 + (z – c)^2 = R^2
]
Xét phương trình sau:
[
x^2 + y^2 + z^2 + 2ax + 2by + 2cz + d = 0
]
Ta có:
[
Rightarrow (x + a)^2 + (y + b)^2 + (z + c)^2 = -d + a^2 + b^2 + c^2
]
Phương trình này là phương trình mặt cầu khi (a^2 + b^2 + c^2 > d). Khi đó, ( (S) ) có tâm (I(-a;-b;-c)) và bán kính (R = sqrt{a^2 + b^2 + c^2 – d}).
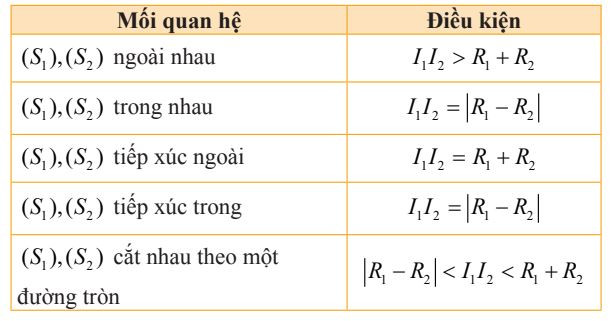Vị trí tương đối của hai mặt cầu
V. Bài tập
Dưới đây là một số dạng toán cơ bản về Hệ tọa độ trong không gian để các em luyện tập:
Bài tập hệ tọa độ trong không gian
Các dạng toán khác về Hệ tọa độ trong không gian được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.
Để lại một bình luận