Diện Tích Xung Quanh và Diện Tích Toàn Phần của Hình Hộp Chữ Nhật: Công Thức và Bài Tập Vận Dụng

Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật là những khái niệm cơ bản trong chương trình Toán học. Việc nắm rõ công thức và cách áp dụng chúng không chỉ giúp các em học sinh làm bài tập tốt hơn mà còn giúp các em vận dụng kiến thức vào thực tiễn. Bài viết dưới đây sẽ cung cấp cho các em công thức tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật, kèm theo các bài tập thực hành có lời giải.

I. Công Thức Tính

1. Diện Tích Xung Quanh

Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp đó.

Để tính diện tích xung quanh của hình hộp chữ nhật, ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).

Cho:

• a: Chiều dài
• b: Chiều rộng
• h: Chiều cao
• Sxq: Diện tích xung quanh
• Cđ: Chu vi đáy

Công thức: Sxq = Cđ x h Hay Sxq = (a + b) x 2 x h

2. Diện Tích Toàn Phần

Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.

Cho:

• Sxq: Diện tích xung quanh hình hộp chữ nhật
• S2đ: Diện tích hai mặt đáy hình hộp chữ nhật
• Stp: Diện tích toàn phần hình hộp chữ nhật

Công thức: Stp = Sxq + S2đ

II. Bài Tập Kèm Đáp Án

📝 Bài 1:

Cho một hình hộp chữ nhật có thể tích bằng 7774 cm³, chiều cao bằng 13 cm, chiều rộng bằng 23 cm. Sxq của hình hộp đó là: ………

Giải:

Công thức tính thể tích hình hộp chữ nhật là:

V = a × b × h

Trong đó:

• V = 7774 cm³ (thể tích)
• b = 23 cm (chiều rộng)
• h = 13 cm

Thay vào công thức trên ta có:

a = V / (b × h) = 7774 / (23 × 13) = 26 cm

Diện tích xung quanh hình hộp chữ nhật là:

Sxq = 2 × (a + b) × h = 2 × (26 + 23) × 13 = 1274 cm².

Vậy diện tích xung quanh của hình hộp chữ nhật là 1274 cm².

📝 Bài 2:

Một bể nước hình hộp chữ nhật có kích thước trong lòng bể như sau: chiều dài 3 m, chiều rộng 1,8 m và cao 1,5 m. Buổi sáng máy bơm đã bơm đầy 90% thể tích bể. Vậy phải bơm thêm …….. lít nước nữa để đầy bể.

Giải:

Thể tích hình hộp chữ nhật được tính theo công thức:

V = a × b × h

Trong đó:

• a = 3 m (chiều dài)
• b = 1,8 m (chiều rộng)
• h = 1,5 m (chiều cao)
• V = 3 × 1,8 × 1,5 = 8,1 m³

Buổi sáng máy bơm đã bơm 90% thể tích bể, nghĩa là:

V đã bơm = 8,1 × 90% = 7,29 m³

Lượng nước cần bơm thêm để đầy bể là:

V cần bơm = 8,1 – 7,29 = 0,81 m³ = 810 lít.

Vậy phải bơm thêm 810 lít nước nữa để đầy bể.

📝 Bài 3:

Một hình hộp chữ nhật có diện tích toàn phần là 336 dm². Tính diện tích xung quanh hình hộp đó biết chiều dài là 2,2 m và chiều rộng là 5 dm.

Giải:

Ta có:

• Chiều dài a = 22 dm
• Chiều rộng b = 5 dm
• Diện tích toàn phần Stp = 336 dm²

Diện tích toàn phần của hình hộp chữ nhật được tính theo công thức:

Stp = Sxq + 2 × S đấy

Diện tích một đáy:

S đáy = a × b = 22 × 5 = 110 dm²

Tổng diện tích hai đáy:

2 × S đáy = 2 × 110 = 220 dm²

Diện tích xung quanh:

Sxq = Stp – 2 × S đáy = 336 – 220 = 116 dm²

Vậy diện tích xung quanh của hình hộp chữ nhật là 116 dm².

📝 Bài 4:

Một căn phòng dạng hình hộp chữ nhật có chiều dài 5 m, chiều rộng 3 m, chiều cao 4 m. Tính diện tích xung quanh và diện tích trần nhà của căn phòng đó.

Giải:

Diện tích xung quanh của hình hộp chữ nhật được tính theo công thức:

Sxq = 2 × (a + b) × h

Trong đó:

• a = 5 m (chiều dài)
• b = 3 m (chiều rộng)
• h = 4 m (chiều cao)

Thay số vào công thức ta có:

Sxq = 2 × (5 + 3) × 4 = 64 m²

Trần nhà có dạng hình chữ nhật với diện tích bằng diện tích đáy của hình hộp chữ nhật:

S trần nhà = a × b = 5 × 3 = 15 m²

Vậy diện tích xung quanh của căn phòng là 64 m² và diện tích trần nhà là 15 m².

III. Bài Tập Vận Dụng

Bài 1: Tính diện tích toàn phần của mỗi hình hộp chữ nhật dưới đây:

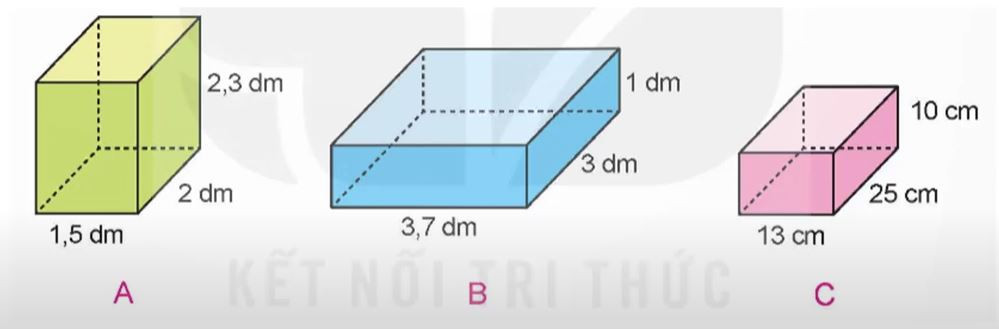Hình minh họa bài 1

Bài 2: Chọn câu trả lời đúng:

Chiếc hộp nào dưới đây có diện tích toàn phần lớn nhất?

Hình minh họa bài 1

Bài 3: Tính diện tích xung quanh của mỗi hình hộp chữ nhật dưới đây:

Hình minh họa bài 1

Bài 4: Các bể cá dưới đây được làm bằng kính và thiết kế dưới dạng hình hộp chữ nhật. Hãy tính diện tích kính cần sử dụng để làm các bể cá đó.

Hình minh họa bài 1

Hy vọng bài viết trên đã giúp các em nắm vững công thức tính toán cũng như biết cách áp dụng vào các bài tập thực tế. Theo dõi loigiaihay.edu.vn để nhận thêm nhiều kiến thức bổ ích khác nhé!