Bài viết này sẽ cung cấp cho các em học sinh lớp 5 một cái nhìn tổng quan về các dạng toán chuyển động, từ cơ bản đến nâng cao, đồng thời giúp các em nắm vững cách giải bài hiệu quả. Các kiến thức này sẽ hỗ trợ các em trong quá trình ôn tập và chuẩn bị cho các bài kiểm tra. Hãy cùng khám phá nhé!
I. Hướng dẫn làm các bài toán chuyển động lớp 5
1. Mối quan hệ giữa quãng đường (s), vận tốc (v) và thời gian (t)
- Mối liên hệ giữa vận tốc, quãng đường và thời gian: Trên cùng một quãng đường thì vận tốc và thời gian có mối liên hệ nghịch với nhau.
- Với cùng một vận tốc thì quãng đường và thời gian có mối liên hệ thuận với nhau.
- Với cùng một thời gian thì quãng đường và vận tốc có mối liên hệ thuận với nhau.
2. Một số dạng toán chuyển động đặc biệt
Chuyển động ngược chiều
Bài toán: Xe thứ nhất xuất phát từ A với vận tốc là a (đơn vị km/g). Cùng lúc đó xe thứ hai xuất phát từ B với vận tốc là b (km/g). Hỏi sau bao lâu hai xe gặp nhau?
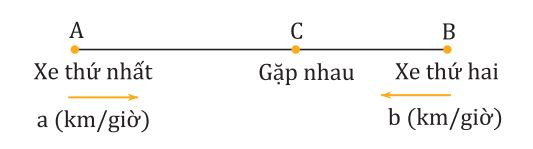 Minh họa cho chuyển động ngược chiều
Minh họa cho chuyển động ngược chiều
- Bước 1: Xác định được khoảng cách của hai xe là AB.
- Bước 2: Tính sau mỗi giá trị khoảng cách khái quát hai xe đi được là: a + b (km).
- Bước 3: Hai xe gặp nhau sau thời gian t = AB / (a + b) (giờ).
Công thức tổng quát:
| Thời gian hai xe đi để gặp nhau = Khoảng cách hai xe : Tổng vận tốc |
|—|
Chuyển động cùng chiều
Bài toán: Xe thứ nhất xuất phát từ A với vận tốc là a (đơn vị km/g), đồng thời xe thứ hai xuất phát từ B với vận tốc là b (km/g) và đi cùng chiều theo xe thứ nhất (xem hình vẽ). Biết b > a. Hỏi xe thứ hai gặp xe thứ nhất sau bao lâu?
- Bước 1: Xác định khoảng cách lúc đầu của hai xe là AB.
- Bước 2: Tính sau mỗi giá trị khoảng cách xe đi gần xe thứ nhất là: b – a (km).
- Bước 3: Xe thứ hai gặp xe thứ nhất sau thời gian t = AB / (b – a) (giờ).
Công thức tổng quát:
| Thời gian hai xe đi để gặp nhau = Khoảng cách hai xe : Hiệu vận tốc |
|—|
II. Các dạng toán chuyển động lớp 5
1. Dạng cơ bản
Các bài toán chuyển động lớp 5 ở dạng cơ bản chủ yếu là các bài toán với các yêu cầu đơn giản, không có nhiều yêu tố phức tạp và cần tính toán trực tiếp.
a) Bài toán Chuyển động đều
Bài toán: Tính quãng đường đi được khi biết thời gian và vận tốc.
Ví dụ: Một chiếc xe chạy với vận tốc 50 km/h trong 3 giờ. Tính quãng đường xe đi được.
Hướng dẫn giải:
Áp dụng công thức tính quãng đường:
( s = v times t = 50 times 3 = 150 , text{km} )Đáp số: 150 km.
b) Bài toán Chuyển động ngược chiều
Bài toán: Tính tổng thời gian khi hai người cùng xuất phát từ hai vị trí khoảng cách nhau một quãng đường nhất định, đi về phía nhau với các vận tốc khác nhau.
Ví dụ: Hai người xuất phát từ hai điểm A và B cách nhau 60 km. Người thứ nhất đi với tốc độ 20 km/h, người thứ hai đi với tốc độ 30 km/h. Hỏi thời gian hai người gặp nhau là bao lâu?
Hướng dẫn giải:
- Tổng vận tốc: ( v_{tổng} = 20 + 30 = 50 text{ km/h} )
- Thời gian gặp nhau: ( t = frac{60}{50} = 1,2 text{ giờ} )
2. Dạng nâng cao
Dạng nâng cao có thể có nhiều yếu tố kết hợp hoặc yêu cầu người học phải áp dụng nhiều bước tính toán, tư duy logic để giải quyết.
a) Bài toán Chuyển động của nhiều đối tượng
Bài toán: Tính quãng đường khi có sự kết hợp giữa nhiều đối tượng chuyển động cùng chiều và ngược chiều.
Ví dụ: Một người đi bộ từ A đến B với vận tốc 4 km/h, trong khi một người khác đi từ B đến A với tốc độ 6 km/h. Hỏi sau bao lâu hai người gặp nhau nếu quãng đường AB là 10 km?
Hướng dẫn giải:
- Tổng vận tốc: ( v_{tổng} = 4 + 6 = 10 text{ km/h} )
- Thời gian gặp nhau: ( t = frac{10}{10} = 1 text{ giờ} )
III. Các bài tập vận dụng
Bài tập giúp các em nắm vững kiến thức và các công thức đã học. Hãy cùng giải quyết các bài tập dưới đây và luyện tập thêm nhé!
- Một ô tô đi từ A đến B trong 1 giờ với vận tốc 60 km/h. Tính quãng đường AB.
- Hai người cùng xuất phát từ hai điểm A và B với khoảng cách nhau 100 km. Nếu một người đi với tốc độ 25 km/h và người còn lại với 35 km/h. Hỏi ai gặp ai đầu tiên?
Hẹn gặp lại các em trong các bài học sau! Đừng quên truy cập vào trang web loigiaihay.edu.vn để cập nhật thêm nhiều bài viết bổ ích khác!
Để lại một bình luận