Bất đẳng thức và bất phương trình là những khái niệm cơ bản nhưng rất quan trọng trong chương trình Toán học tại bậc trung học phổ thông. Kiến thức này xuất hiện trong khoảng 40% các bài toán và câu hỏi trong kỳ thi THPT Quốc Gia. Do đó, nắm vững kiến thức này là điều cần thiết để các em có thể đạt điểm cao trong kỳ thi. Hãy cùng ôn luyện và củng cố kiến thức về bất đẳng thức và bất phương trình ngay nhé!
I. BẤT ĐẲNG THỨC
1. Ôn tập bất đẳng thức
a. Khái niệm bất đẳng thức
Một bất đẳng thức được biểu diễn dưới dạng “a >= b” hay “a <= b”, trong đó a và b là hai giá trị số.
b. Bất đẳng thức hệ quả và bất đẳng thức tương đương
Nếu có bất đẳng thức “a > c”, thì ta có thể viết lại nó thành nhiều dạng khác nhau với các hệ quả tương tự mà vẫn giữ nguyên giá trị.
c. Tính chất của bất đẳng thức
Tính chất của bất đẳng thức cho phép chúng ta so sánh các giá trị cụ thể với nhau. Để minh chứng điều này, chúng ta sử dụng bảng các tính chất của bất đẳng thức.
Bảng tính chất của bất đẳng thức
2. Bất đẳng thức giữa trung bình cộng và trung bình nhân (bất đẳng thức Cô-si)
a. Bất đẳng thức Cô-si
Định nghĩa: Trung bình nhân của hai số không âm luôn ít hơn hoặc bằng trung bình cộng của chúng.
b. Các hệ quả
-
Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2:
[
a + frac{1}{a} geq 2; ; forall a > 0
] -
Nếu x, y cùng dương và tổng không thay đổi thì tích xy lớn nhất khi x = y.
3. Bất đẳng thức chứa cấu giá trị tuyệt đối
| Điều kiện | Nội dung |
|---|---|
| a > 0 | |
II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH CƠ BẢN MỘT ÁN
1. Khái niệm bất phương trình một ẩn
a. Bất phương trình một ẩn
Bất phương trình một ẩn x là một mệnh đề chứa biến có dạng f(x) trong đó f(x) và g(x) là những biểu thức của x.
Giải bất phương trình là tìm tập nghiệm của nó, khi tập nghiệm rộng thì sẽ được gọi là bất phương trình vô nghiệm.
b. Điều kiện của một bất phương trình
Tương tự như phương trình, ta sẽ gán các điều kiện của ẩn số x để f(x) và g(x) có nghĩa.
c. Bất phương trình chứa tham số
Trong một bất phương trình, ngoài các chữ biến còn có thể có các chữ khác được xem như những hằng số. Giải và biện luận bất phương trình chứa tham số là xét xem với các giá trị nào của tham số bất phương trình vẫn có nghiệm.
2. Hệ bất phương trình một ẩn
Hệ bất phương trình một ẩn x gồm một số bất phương trình một ẩn phải tìm nghiệm chung của chúng.
Mỗi giá trị của x đồng thời là nghiệm của tất cả các bất phương trình của hệ được gọi là một nghiệm của hệ bất phương trình đó.
Giải hệ bất phương trình là tìm tập nghiệm của nó.
Để giải một hệ bất phương trình ta giải từng bất phương trình rồi lấy giao của các tập nghiệm.
3. Một số phép biến đổi bất phương trình
a. Bất phương trình tương đương
Hai bất phương trình có cùng tập nghiệm sẽ được nói tới tương đương.
b. Phép biến đổi tương đương
Để giải một bất phương trình (hệ bất phương trình) ta liên tiếp biến đổi nó thành những bất phương trình (hệ bất phương trình) tương đương cho đến khi được bất phương trình đơn giản nhất mà ta có thể viết ngay tập nghiệm.
c. Cộng (trừ)
Hệ bất phương trình hện hai vế của bất phương trình với cùng một biểu thức mà không làm thay đổi điều kiện của bất phương trình.
d. Nhân (chia)
Nếu P(x) không bằng 0, thì P(x)Q(x) cũng có thể được coi là một bất phương trình tương đương.
e. Bình phương
Bình phương hai vế của một bất phương trình còn hai vế không âm thì bất phương trình sẽ được mở rộng thành bất phương trình tương đương.
f. Chú ý
Trong quá trình biến đổi một bất phương trình thành bất phương trình tương đương cần chú ý đến những điều sau:
- Trong một bất phương trình P(x), khi nhân (chia) hai vế cho cùng một số x dương, thì tập nghiệm ban đầu của bất phương trình không thay đổi, nhưng tập nghiệm mới của bất phương trình chuyển biến có thể thay đổi.
- Khi giải một bất phương trình P(x) ta cần phải tính cả nghiệm của bất phương trình mới.
III. DẤU CỦA NHỊ THỨC BẬC NHẤT
1. Định lý về dấu của nhị thức bậc nhất
a. Nhị thức bậc nhất
Xét nhị thức bậc nhất ẩn x có dạng f(x) = ax + b trong đó a,b ∈ R, a ≠ 0.
b. Dấu của nhị thức bậc nhất
- Định lý:
Nhị thức f (x) = ax + b có giá trị cùng dấu với hệ số a khi x lấy các giá trị trong khoảng (-b/a;+∞), trái dấu với hệ số a khi x lấy giá trị trong khoảng (-∞;-b/a).
| x | -∞ | -b/a | +∞ |
|---|---|---|---|
| f (x) = ax + b | trái dấu với a | 0 | Cùng dấu với a |
Minh họa bằng đồ thị:
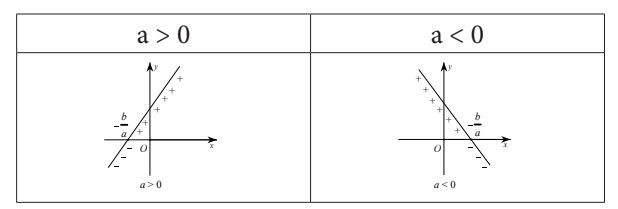Minh họa bằng đồ thị dấu của nhị thức bậc nhất
2. Xét dấu tích thương các nhị thức bậc nhất
Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lý về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử.
Lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương cũng được xét tương tự.
3. Áp dụng và giải bất phương trình
Giải bất phương trình f(x) > 0 thực chất là xét xem biểu thức f(x) nhận giá trị dương với những giá trị nào của x (do đó cũng biết f(x) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức f(x).
a. Bất phương trình tích, bất phương trình chứa ẩn ở mẫu
Ví dụ về bất phương trình chứa ẩn ở mẫu
b. Bất phương trình chứa dấu giá trị tuyệt đối
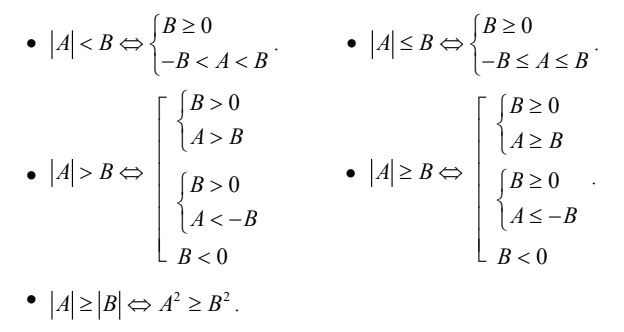Bất phương trình chứa dấu giá trị tuyệt đối
c. Bất phương trình chứa căn thức và dấu giá trị tuyệt đối
Bất phương trình chứa căn thức và dấu giá trị tuyệt đối
d. Các bất phương trình khác
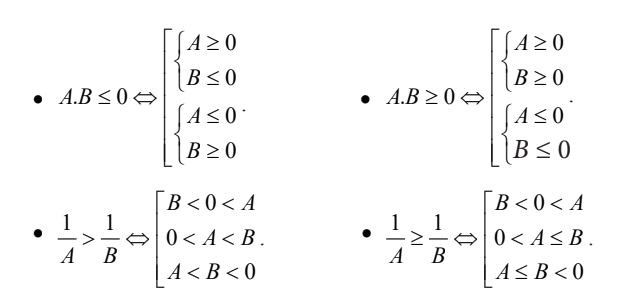Các bất phương trình khác
IV. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
1. Bất phương trình bậc nhất hai ẩn
Bất phương trình bậc nhất hai ẩn x,y có dạng tổng quát là ax + by ≤ c (1)
hoặc (ax + by ≥ c)
Trong đó x, y là hai ẩn; a, b, c là các hệ số (với a² + b² > 0).
Ví dụ về bất phương trình bậc nhất hai ẩn
2. Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn
Cũng như bất phương trình bậc nhất một ẩn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.
Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (1) được gọi là miền nghiệm của nó.
Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình ax + by ≤ c như sau (tương tự cho bất phương trình ax + by ≥ c):
- Bước 1. Trên mặt phẳng tọa độ Oxy, vẽ đường thẳng A: ax + by = c.
- Bước 2. Lấy một điểm M(x0;y0) nằm trong miền (ta thường lấy góc tọa độ 0).
- Bước 3. Tính ax0 + by0, và so sánh ax0 + by0 với c.
- Bước 4. Kết luận.
+ Nếu ax0 + by0 ≤ c thì miền chứa M.
+ Nếu ax0 + by0 > c thì miền không chứa M, là miền nghiệm của ax + by ≥ c.
Chú ý:
Miền nghiệm của bất phương trình ax0 + by0 ≤ c chứa đường thẳng ax + by = c là miền nghiệm của bất phương trình ax0 + by0 > c.
+ Ví dụ:
Biểu diễn hình học tập nghiệm của bất phương trình 2x + y ≤ 3.
Lời giải
Vẽ đường thẳng A:2x + y = 3.
Lấy góc tọa độ O(0;0), ta thấy O ∉ Δ và có 2.0 + 0 ≤ 3.
3. Hệ bất phương trình bậc nhất hai ẩn
Tương tự hệ bất phương trình một ẩn.
Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x,y phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình.
Cũng như bất phương trình bậc nhất bậc hai một ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn.
Ví dụ về hệ bất phương trình bậc nhất hai ẩn
Lời giải
Vẽ các đường thẳng:
- d₁:3x + y = 6
- d₂: x + y = 4
- d₃: x = 0 (Oy)
- d₄: y = 0 (Ox)
Vì điểm M0(1;1) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tồn tại các nửa mặt phẳng không chứa điểm M là miền không thuộc miền nghiệm của hệ đã cho.
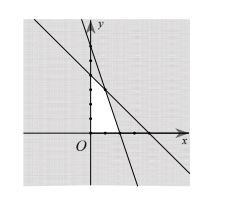Đồ thị miền nghiệm của hệ bất phương trình bậc nhất hai ẩn
V. DẤU CỦA TAM THỨC BẬC HAI
1. Định lý về dấu của tam thức bậc hai
a. Tam thức bậc hai
Xét tam thức bậc hai ẩn x có dạng f(x) = ax² + bx + c , trong đó a,b,c ∈ R, a ≠ 0.
b. Dấu của tam thức bậc hai
Cho f(x) = ax² + bx + c (a ≠ 0); Δ = b² – 4ac
- Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a.
- Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trái dấu khi x = -b/2a.
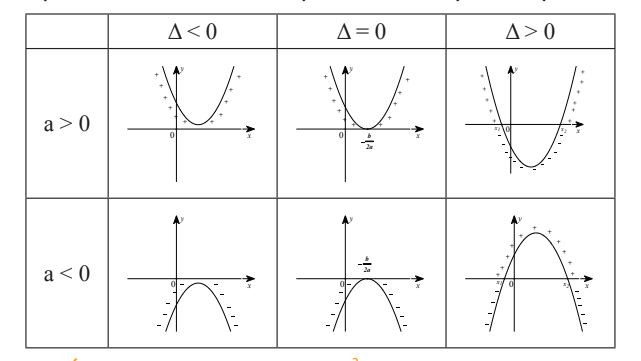Minh họa hình học về dấu của tam thức bậc 2
2. Bất phương trình bậc hai một ẩn
a. Bất phương trình bậc hai
Bất phương trình bậc hai ẩn x có bất phương trình:
ax² + bx + c < 0; ax² + bx + c > 0; ax² + bx + c ≥ 0; ax² + bx + c ≤ 0, trong đó a,b,c ∈ R; a ≠ 0.
b. Giải bất phương trình bậc hai
Giải bất phương trình bậc hai ax² + bx + c < 0, với cùng dấu của hệ số a để quá trình xét dấu từng nghiệp tương tự như dấu tam thức bậc hai.
c. Một số điều kiện tương đương
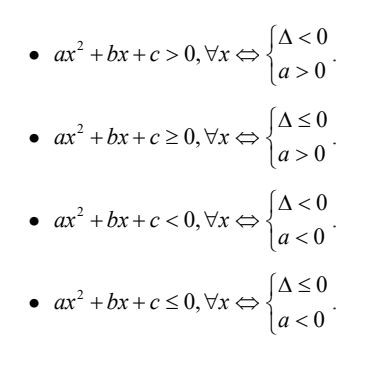Điều kiện tương đương của bất phương trình bậc 2 một ẩn
VI. Một số bài tập về bất đẳng thức và bất phương trình
Dưới đây là một số dạng toán cơ bản về bất đẳng thức và bất phương trình để các em luyện tập và củng cố kiến thức:
Bài tập bất đẳng thức và bất phương trình
Bài tập bất đẳng thức và bất phương trình (tiếp theo)
Các dạng toán khác về bất đẳng thức và bất phương trình được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.
Tkbooks.vn
Để lại một bình luận