Đề thi tuyển sinh vào lớp 10 năm 2023 môn Toán Hà Tĩnh sẽ cung cấp cho các bạn học sinh kiến thức cần thiết để ôn luyện và chuẩn bị cho kỳ thi quan trọng sắp tới. Trong bài viết này, chúng ta sẽ phân tích chi tiết các câu hỏi trong đề thi và đưa ra lời giải cụ thể cho mỗi câu.
I. Đề Thi Tuyển Sinh Vào Lớp 10 Năm 2023 Môn Toán Hà Tĩnh
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau:
a) A = √48 – 3√3
b) B = [1/(√x + 2) + 1/(√x – 2)] : [√x /(x – 4)] (với x > 0; x ≠ 4).
Câu 2. (2,0 điểm)
a) Cho hai đường thẳng (d1): y = (m – 3)x + 4 (m là tham số) và (d2): y = 2x – 1. Tìm giá trị của m để hai đường thẳng (d1) và (d2) song song với nhau.
b) Giải hệ phương trình:
Câu 3. (1,0 điểm)
Cho phương trình x² – 2mx + m² – m – 2 = 0 (m là tham số). Tìm giá trị của m để phương trình đã cho có hai nghiệm phân biệt x1; x2 thỏa mãn:
[(x1x2 + 1)/[x1² + x2² + 2(1 + x1x2)] = 1/6.]
Câu 4. (1,0 điểm)
Một phòng họp ban đầu có 96 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải cắt bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế (số ghế trong các dãy vẫn bằng nhau) để vừa đủ chỗ ngồi cho 110 đại biểu. Hỏi ban đầu trong phòng họp có bao nhiêu dãy ghế?
Câu 5. (1,0 điểm)
Cho tam giác ABC vuông tại A, đường cao AH (H là điểm thuộc BC). Biết độ dài đoạn AB = 5cm và AH = 4cm. Tính độ dài đoạn BH và diện tích tam giác ABC.
Câu 6. (2,0 điểm)
Cho tam giác ABC nhọn. Đường tròn (O) có đường kính BC cắt các cạnh AB, AC lần lượt tại D và E (D khác B và E khác C). Gọi H là giao điểm của hai đường thẳng BE và CD.
a) Chứng minh ADHE là tứ giác nội tiếp.
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tiếp điểm của đường tròn ngoài tiếp tam giác HDP. Chứng minh CE² = BC.MC và ba điểm B, I, P thẳng hàng.
Câu 7. (1,0 điểm)
Cho a, b, c là các số thực khác không. Tìm giá trị nhấn nhất của biểu thức:
[P = frac{a^2}{a^2 + 2(b + c)^2} + frac{b^2}{b^2 + 2(c + a)^2} + frac{c^2}{c^2 + 2(a + b)^2}.]
Đề thi tuyển sinh vào lớp 10 năm 2023 môn Toán Hà Tĩnh
II. Đáp Án Chi Tiết Của Đề Thi Tuyển Sinh Vào Lớp 10 Năm 2023 Môn Toán Hà Tĩnh
Câu 1. (2,0 điểm) Rút gọn các biểu thức sau:
Cách giải:
a) A = √48 – 3√3
Ta có: A = √48 – 3√3 = √(3.16) – 3√3 = 4√3 – 3√3 = √3.
Vậy A = √3.
b) B = [1/(√x + 2) + 1/(√x – 2)] : [√x /(x – 4)] (với x > 0; x ≠ 4).
Với x > 0; x ≠ 4 ta có:
B = [1/(√x + 2) + 1/(√x – 2)] : [√x /(x – 4)]
= [(√x – 2)/[(√x + 2)(√x – 2)] + (√x + 2)/[(√x + 2)(√x – 2)]].(x – 4)/√x
= [(2√x)/[(√x + 2)(√x – 2)]].(x – 4)/√x
= [(2√x)/(x – 4)].(x – 4)/√x
= 2.
Vậy B = 2.
Câu 2. (2,0 điểm)
Cách giải:
a) Để (d1) và (d2) song song với nhau thì m – 3 = 2 và 4 ≠ -1 suy ra m = 5.
Vậy với m = 5 thì hai đường thẳng (d1) và (d2) song song với nhau.
b) Giải hệ phương trình
Hệ phương trình trong câu 2
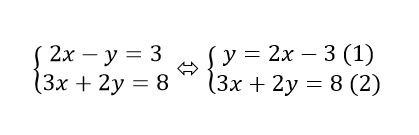Giải hệ phương trình
Thay (1) vào (2) ta có:
(2) ⇒ 3x + 2(2x – 3) = 8 ⇒ 3x + 4x – 6 = 8 ⇒ 7x = 14 ⇒ x = 2.
Thay x = 2 vào (1) ta được y = 2.2 – 3 = 1.
Vậy hệ phương trình có nghiệm (x;y) = (2;1).
Câu 3. (1,0 điểm)
Cách giải:
Ta có Δ’ = m² – (m² – m – 2) = m² – m² + m + 2 = m + 2.
Để phương trình có 2 nghiệm phân biệt thì Δ’ > 0 ⇒ m + 2 > 0 ⇒ m > -2.
Vậy với m > -2 thì phương trình có 2 nghiệm phân biệt x1,x2.
Áp dụng hệ thức Viet:
Để [(x1x2 + 1)/[x1² + x2² + 2(1 + x1x2)] = 1/6,] ta có:
⇒ [(m² – m – 1)/(4m² + 2) = 1/6,]
⇒ (6(m² – m – 1) = 4m² + 2)
⇒ (2m² – 6m – 8 = 0)
⇒ (2(m + 1)(m – 4) = 0)
⇒ (m = -1 text{ hoặc } m = 4.)
Vậy m = -1 hoặc m = 4 thỏa mãn bài toán.
Câu 4. (1,0 điểm)
Cách giải:
Gọi x là số dãy ghế ban đầu. (x > 2, x ∈ N*).
Sau khi cắt đi 2 dãy ghế, số dãy ghế còn lại là: x – 2 (dãy).
Số ghế ở mỗi hàng lúc ban đầu là 96/x (ghế).
Số ghế ở mỗi hàng sau khi cắt bớt hai hàng là 110/(x – 2) (ghế).
Vì khi cắt bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế nên ta có phương trình:
[110/(x – 2) – 96/x = 1,]
⇒ (110x/[(x – 2)x] – [96(x – 2)/[(x – 2)x]] = 1)
⇒ (110x – 96x + 192 = x² – 2x)
⇒ (x² – 16x – 192 = 0)
⇒ ((x – 24)(x + 8) = 0)
Vậy số dãy ghế lúc đầu là 24 dãy ghế.
Câu 5. (1,0 điểm)
Cách giải:
Áp dụng định lý Pytago cho tam giác ABH vuông tại H ta được: (AH² + BH² = AB²)
⇒ (4² + BH² = 5²)
⇒ (16 + BH² = 25)
⇒ (BH² = 9)
⇒ (BH = 3).
Áp dụng hệ thức lưỡng cho tam giác ABC vuông tại A, đường cao AH ta được:
[AB² = BH.BC]
⇒ (BC = AB²/BH = 5²/3 = 25/3).
Diện tích tam giác ABC là: (S.ABC = frac{1}{2} 4 frac{25}{3} = frac{50}{3} (cm²).)
Câu 6. (2,0 điểm)
Cách giải:
a) Chứng minh ADHE là tứ giác nội tiếp.
Ta có gốc BEC = gốc BDC = 90° (gốc nội tiếp chắn trên đường tròn).
⇒ Gốc ADH = gốc AEH = 90°.
⇒ Gốc ADH + gốc AEH = 90° + 90° = 180°.
ADHE là tứ giác nội tiếp (Tứ giác có tổng hai gốc đối bằng 180°).
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tiếp điểm của đường tròn ngoại tiếp tam giác HDP. Chứng minh CE² = BC.MC và ba điểm B, I, P thẳng hàng.
- Hình vẽ minh họa cho câu 6*
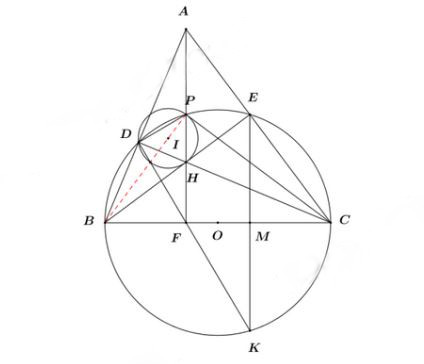Hình vẽ minh họa cho câu 6 – Đề thi tuyển sinh vào lớp 10 năm 2023 môn Toán Hà Tĩnh
+) Chứng minh CE² = BC.MC.
Xét tam giác ABC có: Gốc BEC = gốc BDC = 90° (cmn) ⇒ BE⊥AC, CD⊥AB.
Từ đó, ta có BE nối H và CD nối A => H là trực tâm của tam giác ABC.
Câu 7. (1,0 điểm)
Cách giải:
Áp dụng bất đẳng thức Bu-nhi-a-côp-xki ta có:
((a + b)² ≤ (1+1)(a² + b²) = 2(a² + b²))
((b + c)² ≤ 2(b² + c²))
((c + a)² ≤ 2(c² + a²))
Suy ra P ≥ (frac{a²}{a² + 4(b² + c²)} + frac{b²}{b² + 4(c² + a²)} + frac{c²}{c² + 4(a² + b²)})
= (frac{4(a² + b² + c²)}{3.(a² + 4(b² + c²))} + frac{4(a² + b² + c²)}{3.(b² + 4(c² + a²))} + frac{4(a² + b² + c²)}{3.(c² + 4(a² + b²))} – 1)
= (frac{4}{3}(a² + b² + c²)[{1/(a² + 4(b² + c²))} + {1/(b² + 4(c² + a²))} + {1/(c² + 4(a² + b²))} – 1]
Áp dụng bất đẳng thức cộng mẫu số ta được:
[1/[a² + 4(b² + c²)] + 1/[b² + 4(c² + a²)] + 1/[c² + 4(a² + b²)]≥(1 + 1 + 1)²/[9.(a² + b² + c²)]]
Do đó: (P ≥ frac{4}{3}(a² + b² + c²)[{1/(a² + b² + c²)}] – 1 = frac{4}{3} – 1 = frac{1}{3}.)
Dấu “=” xuất hiện khi và chỉ khi (a = b = c.)
Vậy giá trị nhấn nhất của P là (frac{1}{3}) khi (a = b = c.)
Hy vọng đề thi tuyển sinh vào lớp 10 năm 2023 môn Toán Hà Tĩnh kèm đáp án chi tiết ở trên sẽ giúp các em học sinh lớp 9 tại Hà Tĩnh đã nắm bắt những điểm quan trọng và những kỹ thuật giải toán cần thiết từ đề thi tuyển sinh vào lớp 10 môn Toán năm 2023.
Hãy dành thời gian để luyện tập thật kỹ lưỡng, đặc biệt là những dạng bài đã xuất hiện trong đề thi, để từ đó có thể tự tin giải quyết mọi thử thách trong kỳ thi sắp tới.
Chúc các em ôn tập hiệu quả và đạt được kết quả xuất sắc, mở ra cánh cửa vào những ngôi trường THPT mong muốn.
Tải đề thi dạng PDF tại đây để in và ôn luyện tại nhà nhé!
Tkbooks.vn
Để lại một bình luận