Tính thể tích khối đa diện là một phần rất quan trọng trong chương trình Toán học THPT. Kiến thức về thể tích khối đa diện không chỉ giúp các em học sinh củng cố nền tảng kiến thức của mình mà còn đóng vai trò thiết yếu trong việc giải quyết các bài toán trong kỳ thi THPT Quốc Gia. Với khoảng 10% các bài toán trong đề thi liên quan đến chủ đề này, việc nắm vững kiến thức và công thức tính thể tích là cần thiết để đạt được điểm số mong muốn.
Dưới đây là những kiến thức cơ bản liên quan đến thể tích khối đa diện, giúp các em ôn luyện hiệu quả hơn.
I. Tổng Quan Về Thể Tích Khối Đa Diện
| Hình lăng trụ | Hình có hai đáy là hai đa giác bằng nhau nằm trên hai mặt phẳng song song với nhau và các mặt bên đều là các hình chữ nhật. |
|---|
1. Hình Lăng Trụ Đứng
- Định nghĩa: Hình lăng trụ đứng là hình lăng trụ mà có các cạnh bên vuông góc với mặt đáy.
- Tính chất: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.
2. Hình Lăng Trụ Nghiêng
- Định nghĩa: Hình lăng trụ nghiêng là hình lăng trụ mà không có cạnh bên nào vuông góc với mặt đáy.
- Tính chất: Các mặt bên của hình lăng trụ nghiêng không nhất thiết phải là hình chữ nhật, mà chỉ cần có 2 đáy là đa giác bằng nhau là đủ.
| Hình hộp | Hình lăng trụ có đáy là hình bình hành. |
|---|
3. Hình Hộp Đứng
- Định nghĩa: Hình hộp đứng là hình có các mặt bên vuông góc với mặt đáy.
- Tính chất: Hình hộp đứng có 2 đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.
4. Hình Hộp Chữ Nhật
- Định nghĩa: Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
- Tính chất: Hình hộp chữ nhật có 6 mặt là 6 hình chữ nhật.
5. Hình Lập Phương
- Định nghĩa: Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.
- Tính chất: Hình lập phương có 6 mặt đều là hình vuông.
| Hình chóp | Hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh. |
|---|
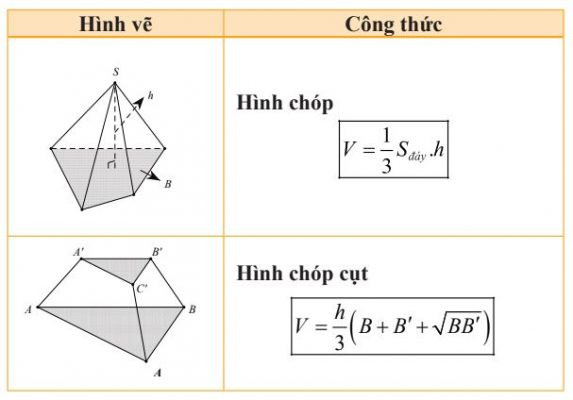
II. Công Thức Tính Thể Tích
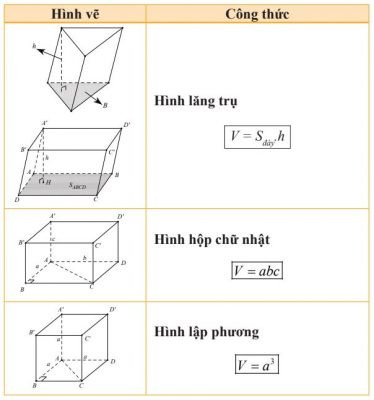Công thức tính thể tích cơ bản (tiếp theo)
Một số công thức tính nhanh thể tích các hình khối thường gặp:
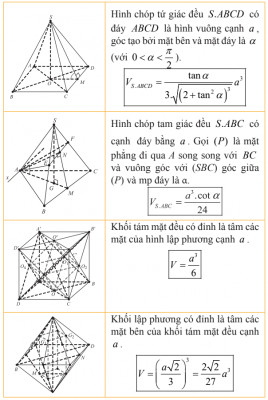Công thức tính nhanh thể tích một số hình khối thường gặp (tiếp)
Một số công thức về hình khối đặc biệt liên quan khối tròn xoay:
Bài tập ví dụ về tính thể tích khối chóp
III. Một số Kết Quả của Các Khối Đa Diện Đặc Biệt
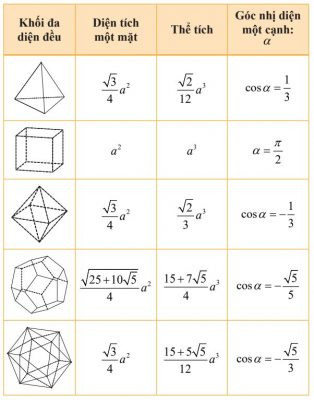Một số kết quả của các khối đa diện đều đặc biệt
IV. Công Thức Tính Nhanh Thể Tích Một Số Khối Tứ Diện Đều Đặc Biệt
Công thức tính nhanh thể tích một số khối tứ diện đều đặc biệt (tiếp theo)
V. Tỷ Số Thể Tích
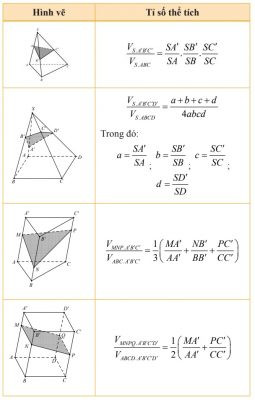Tỷ số thể tích
VI. Bài Tập
Dưới đây là một số dạng toán cơ bản về Thể tích khối đa diện để các em luyện tập:
Bài tập về thể tích khối đa diện
Các dạng toán khác về Thể tích khối đa diện được ghi chú và diễn giải rất đầy đủ trong cuốn sách Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.
Tkbooks.vn
Để lại một bình luận