Khối Đa Diện: Tính Chất và Ứng Dụng Của Phép Đa Diện

Khối đa diện là một khái niệm quan trọng trong chương trình Toán học Trung học phổ thông. Kiến thức này không chỉ xuất hiện trong các bài toán mà còn là nền tảng cho nhiều ứng dụng trong thực tiễn. Trong bài viết này, chúng ta sẽ cùng khám phá sâu hơn về khối đa diện, tính chất của nó cũng như cách ứng dụng trong việc giải các bài toán liên quan.

Khối đa diện có mặt trong khoảng 10% câu hỏi trong đề thi THPT Quốc Gia, vì vậy việc nắm chắc kiến thức này là rất cần thiết để đạt được điểm số tối ưu.

I. Khái Niệm và Phân Loại Khối Đa Diện

1. Khối Đa Diện Là Gì?

Khối đa diện là một khối không gian được giới hạn bởi một số đa giác, trong đó mỗi đa giác là một mặt của khối. Khối đa diện có thể được phân loại thành các loại sau:

• Khối lăng trụ: là phần không gian được giới hạn bởi hai mặt đáy là đa giác và các mặt bên là hình chữ nhật.
• Khối chóp: là phần không gian được giới hạn bởi một mặt đáy là đa giác và các mặt bên là tam giác.

Để hiểu rõ hơn về khối đa diện, hãy xem hình ảnh minh họa dưới đây:

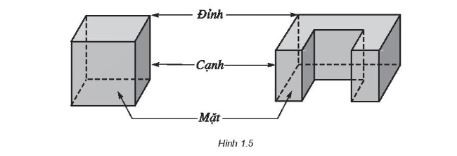Hình minh họa khối đa diện

2. Các Đặc Điểm Của Khối Đa Diện

• Số mặt: Mỗi khối đa diện đều có ít nhất 4 mặt. Những mặt này có thể là các đa giác khác nhau.
• Số đỉnh: Số đỉnh của một khối đa diện tối thiểu là 4 và phụ thuộc vào số mặt và dạng hình học của khối.
• Số cạnh: Số cạnh được tính bằng tổng số cạnh của mọi mặt của khối.

II. Các Phép Biến Hình Trong Không Gian

Khối đa diện có thể được biến đổi thông qua các phép biến hình khác nhau, bao gồm nhưng không giới hạn ở:

1. Phép Dịch Hình

Phép dịch là phép biến hình mà mọi điểm của khối đều được dịch chuyển theo một vectơ cố định.

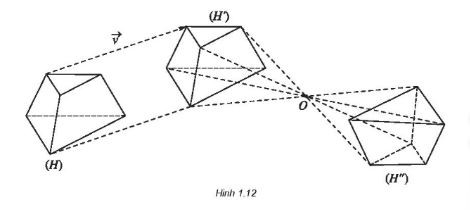Phép dịch hình

2. Phép Đối Xứng

Phép đối xứng là phép biến hình mà một khối được phản ánh qua một mặt phẳng. Điều này có nghĩa là nếu một điểm M thuộc khối, thì điểm M’ cũng sẽ thuộc khối và nằm đối xứng với M qua mặt phẳng đó.

3. Phép Xoay

Phép xoay là phép biến hình mà khối được xoay quanh một trục trong không gian, tạo thành các hình ảnh mới.

III. Hai Đa Diện Bằng Nhau

Hai khối đa diện được gọi là bằng nhau nếu có một phép biến hình biến khối này thành khối kia. Các khối này cũng chia sẻ nhiều tính chất quan trọng.

1. Điều Kiện Bằng Nhau

Hai khối đa diện bằng nhau nếu:

• Chúng có số mặt và số đỉnh giống nhau.
• Có chiều dài cạnh tương ứng bằng nhau.

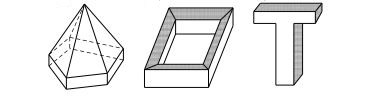Khối đa diện bằng nhau

IV. Phân Chia và Ghép Khối Đa Diện

Khối đa diện có thể được phân chia thành các khối đa diện nhỏ hơn hoặc ghép lại từ các khối khác. Điều này rất hữu ích trong việc giải quyết bài toán và ứng dụng thực tế.

Các Phương Pháp Phân Chia

• Phân chia theo mặt: Chia một khối thành hai khối đa diện mà không có điểm chung nào.
• Ghép lại: Kết hợp hai khối đa diện để tạo thành một khối lớn hơn.

V. Kết Luận

• Mỗi khối đa diện đều có ít nhất 4 mặt và là những hình học cơ bản dùng để giải quyết nhiều bài toán.
• Áp dụng kiến thức về khối đa diện không chỉ giúp nâng cao kỹ năng giải toán mà còn áp dụng vào các vấn đề thực tiễn trong kiến trúc, xây dựng và nghệ thuật.

Hy vọng rằng bài viết này sẽ giúp các bạn củng cố kiến thức về khối đa diện. Để tìm hiểu thêm và thực hành nhiều bài tập phong phú, các bạn hãy truy cập vào loigiaihay.edu.vn để có thêm tài liệu học tập bổ ích!