Hàm số lượng giác và phương trình lượng giác cơ bản

Kiến thức về hàm số lượng giác và phương trình lượng giác là một phần rất quan trọng trong chương trình Toán học THPT. Kiến thức này xuất hiện trong khoảng 15% các bài toán và câu hỏi trong đề thi THPT Quốc Gia, vì vậy các em cần nắm chắc phần này để đạt được điểm số tốt nhất.

Dưới đây là toàn bộ kiến thức về hàm số lượng giác và phương trình lượng giác. Các em hãy lưu lại và ôn luyện thường xuyên để nắm chắc kiến thức nhé!

I. HÀM SỐ LƯỢNG GIÁC

1. Định nghĩa

a) Hàm số sin

Quy tắc đặt tương ứng giữa mỗi số thực x với số thực sin x

• sin x: R → R
• x ↦ y = sin x

Được gọi là hàm số sin, ký hiệu: y = sin x.

Tập xác định là: R.

b) Hàm số cos

Quy tắc đặt tương ứng giữa mỗi số thực x với số thực cos x

• cos x: R → R
• x ↦ y = cos x

Được gọi là hàm số cos, ký hiệu: y = cos x.

Tập xác định là: R.

c) Hàm số tang

Là hàm số được xác định bởi y = sin x/cos x (cos x ≠ 0), ký hiệu y = tan x.

d) Hàm số cotang

Là hàm số được xác định bởi y = cos x/sin x, ký hiệu y = cot x.

Tập xác định là: D = R{kπ, k∈Z}

2. Tính tuần hoàn và chu kỳ của hàm số lượng giác

a) Định nghĩa

Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại một số T ≠ 0 sao cho với mọi x ∈ D, ta có:

x – T ∈ D và x + T ∈ D

f(x + T) = f(x)

Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kỳ của hàm số tuần hoàn đó.

Người ta chứng minh được rằng hàm số y = sin x tuần hoàn với chu kỳ T = 2π; hàm số y = cos x tuần hoàn với chu kỳ T = 2π; hàm số y = tan x tuần hoàn với chu kỳ T = π; hàm số y = cot x tuần hoàn với chu kỳ T = π.

Tính tuần hoàn và chu kỳ của hàm số lượng giác

3. Sự biến thiên và đồ thị của hàm số lượng giác

a) Hàm số y = sin x

• Tập xác định: D = R, có nghĩa là xác định với mọi x∈R;
• Tập giá trị: T = [-1; 1], nghĩa là [-1, 1];
• Hàm số tuần hoàn với chu kỳ 2π, nghĩa là sin(x + k2π) = sin x với k∈Z.
• Hàm số đồng biến trên mọi khoảng (-π/2 + k2π; π/2 + k2π) và nghịch biến trên mọi khoảng (π/2 + k2π; 3π/2 + k2π), k∈Z.
• Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng.

Sự biến thiên của hàm số y = sin x

b) Hàm số y = cos x

• Tập xác định: D = R, có nghĩa là xác định với mọi x∈R.
• Tập giá trị: T = [-1; 1], nghĩa là [-1, 1];
• Hàm số tuần hoàn với chu kỳ 2π, nghĩa là cos(x + k2π) = cos x với k∈Z.
• Hàm số đồng biến trên mọi khoảng (-π + k2π; k2π) và nghịch biến trên mọi khoảng (k2π; π + k2π), k∈Z.
• Là hàm số chẵn nên đồ thị hàm số nhận gốc tọa độ O là trục đối xứng.

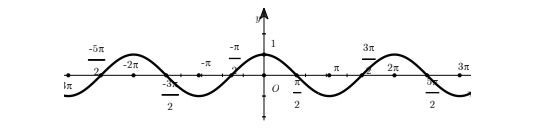Sự biến thiên của hàm số y = cos x

c) Hàm số y = tan x

• Tập xác định: D = R{π/2 + kπ, k∈Z}.
• Tập giá trị: T = R
• Hàm số tuần hoàn với chu kỳ π, nghĩa là tan(x + kπ) = tan x với k∈Z.
• Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng.

Sự biến thiên của hàm số y = tan x

d) Hàm số y = cot x

• Tập xác định: D = R{kπ, k∈Z}
• Tập giá trị: T = R
• Hàm số tuần hoàn với chu kỳ π, nghĩa là cot(x + kπ) = cot x với k∈Z.
• Hàm số đồng biến trên mọi khoảng (kπ; (k + 1)π), k∈Z.
• Là hàm số lẻ nên đồ thị hàm số nhận gốc tọa độ O là tâm đối xứng.

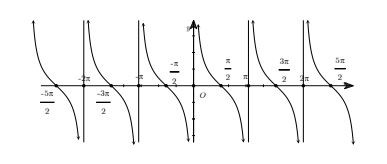Sự biến thiên của hàm số y = cot x

II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

1. Phương trình sin x = a

• Trường hợp |a| > 1 → phương trình vô nghiệm vì -1 < sin x < 1
• Trường hợp |a| ≤ 1 → phương trình có nghiệm, cụ thể: a∈{0; ±1/2; ±√2/2; ±√3/2; ±1}

Khi đó:

Nghiệm của phương trình sin x = a

sinu = -sin v ⇒ sinu = sin (-v)

sin u = cos v ⇒ sin u = sin (π/2 – v)

sinu = – cos v ⇒ sin u = sin (v – π/2)

CÁc trường hợp đặc biệt:

sin x = 0 ⇒ x = kπ (k ∈ Z).

sin x = 1 ⇒ x = π/2 + k2π (k ∈ Z).

sin x = -1 ⇒ x = -π/2 + k2π (k ∈ Z).

2. Phương trình cos x = a

• Trường hợp |a| > 1 → phương trình vô nghiệm, vì -1 < cos x < 1
• Trường hợp |a| ≤ 1 → phương trình có nghiệm cụ thể:

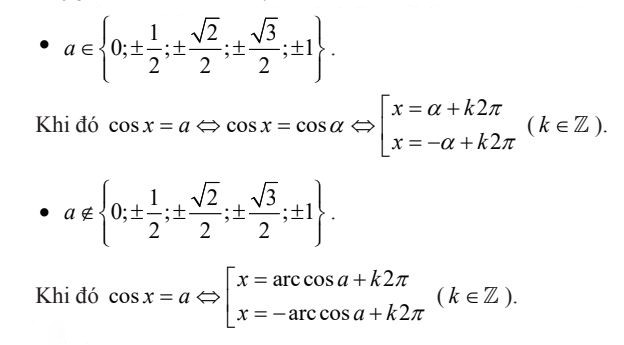Nghiệm của phương trình cos x = a

CÁc trường hợp đặc biệt:

cosu = -cos v ⇒ cos u = cos(π – v).

cos u = sin v ⇒ cos u = cos (π/2 – v)

cos u = -sin v ⇒ cos u = cos (π/2 + v).

CÁc trường hợp đặc biệt:

cos x = 0 ⇒ x = π/2 + kπ, (k ∈ Z).

cos x = 1 ⇒ x = k2π, (k ∈ Z).*

cos x = -1 ⇒ x = π + k2π, (k ∈ Z).*

3. Phương trình tan x = a

Điều kiện: x ≠ π/2 + kπ, (k ∈ Z).

Khi đó:

Nghiệm của phương trình tan x = a

CÁc trường hợp đặc biệt:

tan u = – tan v ⇒ tan u = tan(-v).

tan u = cot v ⇒ tan u = tan (π/2 – v).

tan u = – cot v ⇒ tan u = tan (π/2 + v).

CÁc trường hợp đặc biệt:

tan x = 0 ⇒ x = kπ, (k ∈ Z).

tan x = ±1 ⇒ x = π/4 ± kπ, (k ∈ Z).

4. Phương trình cot x = a

Điều kiện: x ≠ kπ + π, (k ∈ Z).

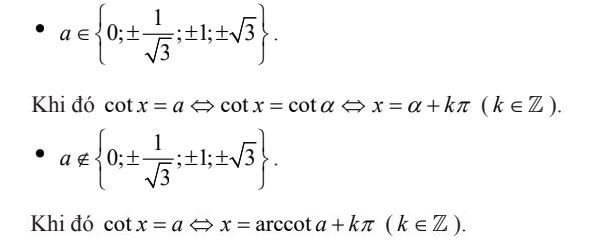Nghiệm của phương trình cot x = a

CÁc trường hợp đặc biệt:

cot x = 1 ⇒ x = π/4 + kπ, (k ∈ Z).

cot x = -1 ⇒ x = -π/4 + kπ, (k ∈ Z).

cot x = 0 ⇒ x = π/2 + kπ, (k ∈ Z).

III. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP

1. Phương trình bậc nhất đối với sin x và cos x

Phương trình có dạng:

a sin x + b cos x = c

Phương pháp: Điều kiện để phương trình có nghiệm:

a² + b² ≥ c².

Cách giải phương trình bậc nhất đối với sin x và cos x

2. Phương trình bậc hai đối với một hàm số lượng giác

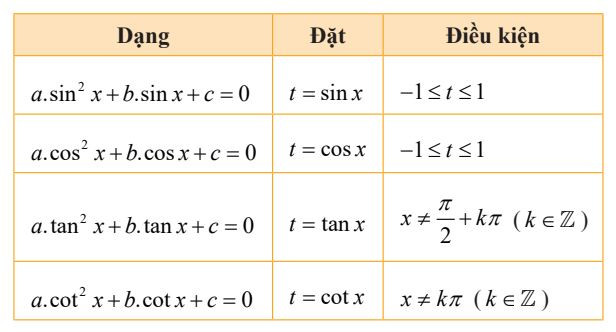Phương trình bậc hai đối với một hàm số lượng giác

3. Phương trình tuần hoàn bậc hai đối với sin x và cos x

Phương trình có dạng:

a sin² x + b sin x cos x + c cos² x = 0

Phương pháp:

Kiểm tra cos x = 0 có phải nghiệm của phương trình không?

Khi cos x ≠ 0, chia hai vế phương trình cho cos² x ta được phương trình:

a tan² x + b tan x + c = 0.

Đây là phương trình bậc hai đối với tan x mà ta đã biết cách giải.

4. Phương trình tuần hoàn bậc ba đối với sin x và cos x

Phương trình có dạng:

a.sin³ x + b.sin x cos² x + c. sin x cos² x + d.cos³ x + e.sin x + f.cos x = 0

Phương pháp:

• Kiểm tra cos x = 0 có phải nghiệm của phương trình không?
• Khi cos x ≠ 0, chia hai vế phương trình cho cos³ x ta được phương trình:

1/cos² x = 1 + tan² x

Một số điều cần chú ý khi giải phương trình lượng giác:

Khi giải phương trình có chứa các hàm số tan, cot, có mẫu số hoặc chứa căn bậc chắn, thì nhất thiết phải đặt điều kiện để phương trình xác định.

Một số điều cần chú ý khi giải phương trình lượng giác (tiếp theo)

5. Một số bài tập về hàm số lượng giác và phương trình lượng giác

Dưới đây là một số dạng toán cơ bản về hàm số lượng giác và phương trình lượng giác để các em luyện tập:

1. Bài tập về hàm số lượng giác

Bài tập về hàm số lượng giác

Bài tập về hàm số lượng giác (tiếp theo)

2. Bài tập về phương trình lượng giác

Bài tập về phương trình lượng giác

Bài tập về phương trình lượng giác (tiếp theo)

Các dạng toán khác về hàm số lượng giác và phương trình lượng giác được ghi chú và diễn giải rất đầy đủ trong cuốn Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!

Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.

Tkbooks.vn