Trong chương trình Toán lớp 9, hàm số bậc 2 đóng vai trò quan trọng, giúp học sinh hiểu sâu sắc hơn về mối quan hệ giữa biến số và các hình dạng đồ thị. Đây cũng là phần kiến thức trọng tâm trong học kỳ 2 lớp 9 mà chắc chắn các em sẽ gặp trong các bài thi và bài kiểm tra.
Hãy cùng Tkbooks tìm hiểu về hàm số bậc 2 y = ax² (a ≠ 0) và đồ thị của nó qua bài viết dưới đây cũng như tham khảo các dạng bài tập cơ bản về hàm số bậc 2 nhé!
I. Lý Thuyết Hàm Số Bậc 2
-
Hàm số bậc 2 có dạng y = ax² (a ≠ 0) có tính chất:
-
Nếu a > 0 thì hàm số nghịch biến khi x < 0.
-
Nếu a < 0 thì hàm số đồng biến khi x < 0.
-
-
Đồ thị hàm số bậc 2 y = ax² (a ≠ 0) là một đường cong đi qua gốc tọa độ O và nhận Oy làm trục đối xứng.
- Nếu a > 0 thì đồ thị lồi lên trên, và đồ thị ở phía trên trục hoành.
Đồ thị hàm số bậc 2 khi a > 0
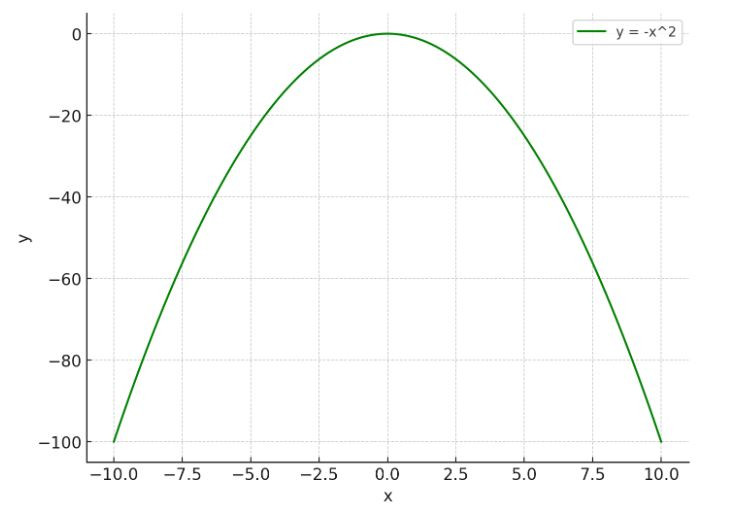
- Nếu a < 0 thì đồ thị lõm xuống dưới, và đồ thị ở phía dưới trục hoành.
Đồ thị hàm số bậc 2 khi a < 0
II. Bài Tập Về Hàm Số Bậc 2 Lớp 9 y = ax²
Dạng 1: Tính giá trị của hàm số y = f(x) = ax² (a ≠ 0) tại x = x0 và ngược lại
+ Phương pháp
Thay x = x0 vào y = f(x0) hoặc ngược lại thay giá trị của hàm số vào để tìm x.
+ Các ví dụ
Ví dụ 1: Cho hàm số y = f(x) = (-1/2)x². Hãy tính các giá trị f(-4); f(-1); f(0); f(1); f(4).
Lời giải:
Ta có: f(-4) = (-1/2).(-4)² = -8;
f(-1) = -1/2; f(0) = 0; f(1) = (-1/2); f(4) = -8.
Ví dụ 2: Cho hàm số y = (1/3)x². Tìm các giá trị của x biết rằng:
a) y = 1/27;
b) y = 12.
Lời giải:
a) y = 1/27 ⇒ (1/3)x² = 1/27 ⇒ x = ± 1/3.
b) y = 12 ⇒ (1/3)x² = 12 ⇒ x = ± 6.
Dạng 2: Tính đạo hàm, nghịch biến của hàm số
+ Phương pháp
Dựa vào tính chất của hàm số y = ax² (a ≠ 0):
- a > 0 thì hàm số nghịch biến khi x < 0.
- a < 0 thì hàm số đồng biến khi x < 0.
+ Các ví dụ
Ví dụ 3: Cho hàm số y = (2m – 1)x² với m ≠ 1/2.
a) Tìm các giá trị của m để hàm số nghịch biến với x > 0.
b) Tìm các giá trị của m để hàm số đồng biến với x > 0.
Lời giải:
a) Để hàm số nghịch biến với x > 0 thì 2m – 1 < 0.
b) Để hàm số đồng biến với x > 0 thì 2m – 1 > 0 ⇒ m > 1/2.
Dạng 3: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = ax² (a ≠ 0)
+ Phương pháp
Cho hàm số y = ax² (a ≠ 0):
Nếu a > 0 thì y ≥ 0 với mọi x. Giá trị nhỏ nhất của hàm số là y = 0 khi x = 0.
Nếu a < 0 thì y ≤ 0 với mọi x. Giá trị lớn nhất của hàm số là y = 0 khi x = 0.
+ Các ví dụ
Ví dụ 5: Cho hàm số y = (m² – 4)x². Tìm giá trị của m để:
a) Hàm số có giá trị lớn nhất là 0;
b) Hàm số có giá trị nhỏ nhất là 0.
Lời giải:
a) Hàm số có giá trị lớn nhất là 0 khi m² – 4 < 0.
b) Hàm số có giá trị nhỏ nhất là 0 khi m² – 4 > 0 ⇒ m > 2 hoặc m < -2.
Dạng 4: Điểm thuộc đồ thị. Vẽ đồ thị hàm số y = ax² (a ≠ 0)
+ Phương pháp
Cho hàm số y = ax² (a ≠ 0) có đồ thị là Parabol (P):
-
Điểm M có tọa độ (x0;y0) thuộc đồ thị parabol (P) khi và chỉ khi y0 = ax0².
-
Điểm M có tọa độ (x0;y0) không thuộc đồ thị parabol (P) khi y0 ≠ ax0².
- Vẽ đồ thị hàm số y = ax² (a ≠ 0).
+ Các ví dụ
Ví dụ 7: Cho hàm số y = (1/2)x².
a) Vẽ đồ thị hàm số.
b) Các điểm M(2;2), N(-1;4); P(1;½) có thuộc đồ thị hàm số trên không?
c) Tìm các giá trị m và n để các điểm M(4;m) và N(n;1) thuộc đồ thị hàm số trên.
Lời giải:
a) Học sinh tự vẽ đồ thị.
b) Vì (1/2).2² = 2 nên điểm M(2;2) thuộc đồ thị hàm số.
Tương tự, điểm N(-1;4) không thuộc và điểm P(1;½) thuộc đồ thị hàm số.
c) Điểm M(4;m) thuộc đồ thị hàm số ⇒ (1/2).4² = m ⇒ m = 8.
Điểm N(n;1) thuộc đồ thị hàm số ⇒ (1/2).n² = 1 ⇒ n = ±√2.
Ví dụ 8: Tìm giá trị của m để hàm số y = (m-1)x² đi qua điểm A(2;12).
Lời giải:
Để hàm số đi qua điểm A(2;12) thì (m – 1).2² = 12 ⇒ m = 4.
Ví dụ 9: Tìm hệ số a biết rằng đồ thị hàm số (P): y = ax² và đường thẳng (d): y = 2x – 3 cắt nhau tại điểm có hoành độ bằng -1.
Lời giải:
Xét phương trình hoành độ giao điểm của (P) và (d) có: ax² = 2x – 3.
Vì đồ thị hàm số (P) và đường thẳng (d) cắt nhau tại điểm có hoành độ bằng -1 nên a.(-1)² = 2.(-1) – 3 ⇒ a = -5.
Ví dụ 10: Tìm a biết rằng hàm số (P): y = (2a + 5)x² và đường thẳng (d): y = 3x + 1 cắt nhau tại điểm có tung độ bằng 4.
Lời giải:
Gọi A (xA, yA) là giao điểm của hàm số y = (2a + 5)x² và (d).
Vì đồ thị hàm số (P) và đường thẳng (d) cắt nhau tại điểm có tung độ bằng 4 nên yA = 4 ⇒ 4 = 3xA + 1 ⇒ xA = 1.
Thay xA = 1 vào y = (2a + 5)x² ta được 4 = (2a + 5).1² ⇒ a = -1/2.
III. Bài Tập Thực Hành Thêm:
Dưới đây là một số bài tập thực hành thêm về hàm số bậc 2 lớp 9 để các em làm ở nhà:
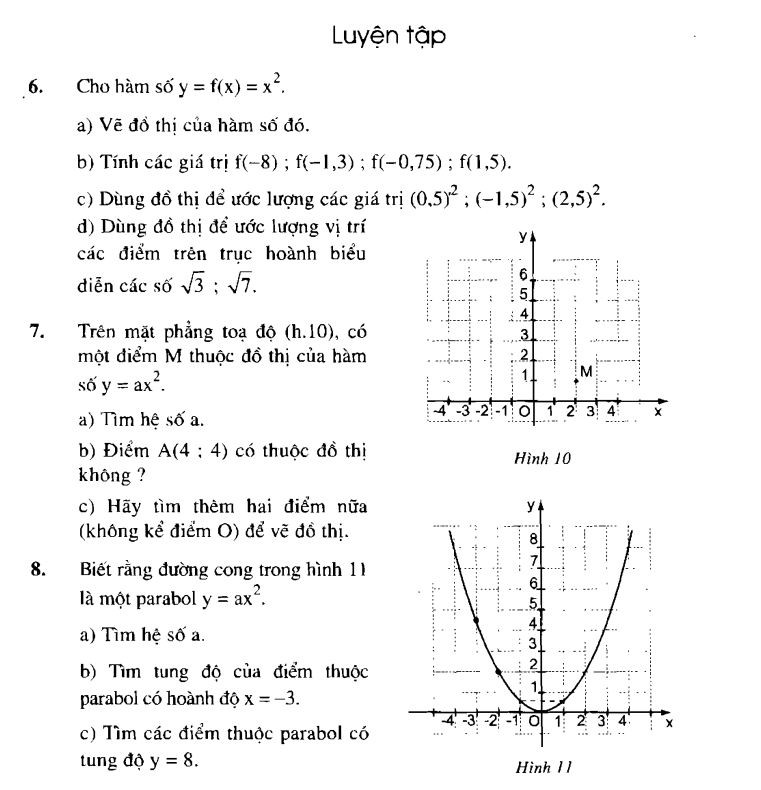Bài tập thực hành thêm về hàm số bậc 2 lớp 9
Hy vọng những kiến thức về hàm số bậc 2 lớp 9 ở trên sẽ giúp các em đạt điểm số cao hơn trong các bài thi và bài kiểm tra Toán trên lớp.
Để tìm hiểu thêm về kiến thức Toán lớp 9 trong học kỳ 2, các em nên mua cuốn sách Làm chủ kiến thức Toán 9 ôn thi vào 10 phần Đại số của Tkbooks nhé!
Link để tải sách: https://drive.google.com/file/d/1uaOJCek1Mpmm-UbFU3hEIVzQ0P6PPaoC/view
TKbooks tự hào là nhà xuất bản sách tham khảo cho học sinh THCS hàng đầu tại Việt Nam.
TKbooks.vn
Để lại một bình luận