Hàm số bậc 1 – Lý thuyết, các dạng toán và cách giải cực chi tiết

Hàm số bậc 1 là một trong những kiến thức trọng tâm trong chương trình toán học lớp 9. Việc hiểu rõ về hàm số bậc 1 không chỉ giúp học sinh nắm vững lý thuyết mà còn hỗ trợ trong việc giải quyết các bài toán liên quan trong kỳ thi. Bài viết dưới đây sẽ cung cấp cái nhìn tổng quát và chi tiết nhất về hàm số bậc 1, bao gồm định nghĩa, các dạng toán cơ bản và phương pháp giải.

I. Hàm số bậc 1 là gì?

Hàm số bậc 1 (hay còn gọi là hàm số bậc nhất) có dạng tổng quát:
[ y = ax + b quad text{với } a neq 0 ]

• Điều kiện và Đặc điểm:

  • Hàm bậc 1 xác định với mọi giá trị của x thuộc tập số thực ( mathbb{R} ).
  • Tính chất đồng biến của hàm số phụ thuộc vào giá trị của a:
    • Nếu ( a > 0 ) thì hàm đồng biến.
    • Nếu ( a < 0 ) thì hàm nghịch biến.

• Đồ thị:

  • Đồ thị của hàm số bậc 1 là một đường thẳng. Nó sẽ cắt trục tung tại điểm có tung độ b, và có độ dốc ( a ).
  • Khi ( a = 0 ), đồ thị trở thành đường thẳng nằm ngang, tạo với trục Ox một góc bằng 0.

• Mối quan hệ giữa các đường thẳng:

  • Giả sử có hai hàm số bậc 1: ( d: y = ax + b ) và ( d’: y = a’x + b’ ) với ( a neq a’ ) và ( b neq b’ ):
    • Hai đường thẳng song song nếu ( a = a’ ) và ( b neq b’ ).
    • Hai đường thẳng trùng nhau nếu ( a = a’ ) và ( b = b’ ).
    • Hai đường thẳng cắt nhau nếu ( a neq a’ ).
    • Hai đường thẳng vuông góc nếu ( aa’ = -1 ).

II. Các dạng toán cơ bản về hàm số bậc 1 và cách giải

1. Dạng 1: Nhận dạng hàm số bậc 1

+ Phương pháp

Để nhận diện hàm số bậc 1, cần xác định rằng nó có dạng:
[ y = ax + b quad text{với } a neq 0 ]
Một hàm số bậc nhất có thể biểu thị một dạng khác, nhưng phải quy về được dạng trên.

Hàm số bậc nhất là kiến thức quan trọng xuất hiện rất nhiều trong các bài thi

+ Ví dụ

• Ví dụ 1:
  • Cho các hàm số sau, xác định đâu là hàm số bậc nhất và chỉ ra hệ số a, b của nó:
    • a) ( y = 5 – 3x );
    • b) ( y = 10x^2 – 9 );
    • c) ( y = 3(x-1) – x );
    • d) ( y = x^3 + 1 );
    • e) ( y = frac{x + 1}{sqrt{3}} );
    • f) ( y = 1 – frac{(4x + 1)}{3} );
    • g) ( y = frac{1}{x} + x );
    • h) ( y = 2(x – 1) + sqrt{3} ).

Lời giải:

• Hàm số bậc 1 là a, c, e, f, h.

2. Dạng 2: Tìm tham số m để hàm số là hàm số bậc 1

+ Phương pháp

Bước 1: Đưa hàm số đã cho về dạng ( y = ax + b ) và xác định hệ số ( a ).
Bước 2: Tìm điều kiện cho ( a neq 0 ) để hàm số trở thành hàm bậc nhất.

+ Ví dụ

• Ví dụ 2:
  • Tìm các giá trị của tham số m để các hàm số sau trở thành hàm số bậc nhất:
    • a) ( y = (2m – 3)x – 1 );
    • b) ( y = sqrt{m – 2}(x – 1) );
    • c) ( y = frac{(sqrt{m} + 1)}{(sqrt{m} – 1)} x + 1 );
    • d) ( y = m(1 – x) + m – x ).

Lời giải:

• a) hàm bậc nhất khi ( 2m – 3 neq 0 );
• b) hàm bậc nhất khi ( m > 2 );
• c) hàm bậc nhất khi ( m geq 0 ) và ( m neq 1 );
• d) hàm bậc nhất khi ( m neq – 1 ).

3. Dạng 3: Xét tính đồng biến, nghịch biến của hàm số bậc 1

+ Phương pháp

Khi có hàm số ( y = ax + b ) (với ( a neq 0 )):

• Hàm đồng biến khi ( a > 0 )
• Hàm nghịch biến khi ( a < 0 )

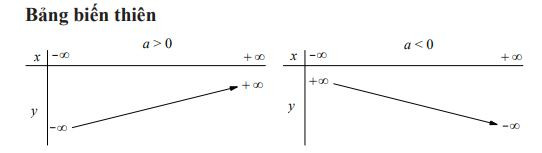Bảng biến thiên của hàm số bậc 1

+ Ví dụ

• Ví dụ 4:
  • So sánh tính đồng biến, nghịch biến giữa hai hàm số ( y = 2x – 4 ) và ( y = -3x + 5 ):

Lời giải:

• Hàm số ( y = 2x – 4 ) đồng biến vì ( a = 2 > 0 ).
• Hàm số ( y = -3x + 5 ) nghịch biến vì ( a = -3 < 0 ).

4. Dạng 4: Vẽ đồ thị của hàm số bậc 1

+ Phương pháp

• Đồ thị của hàm số ( y = ax + b ) là một đường thẳng.
• Cắt trục tung tại điểm có tung độ b và cắt trục hoành tại điểm có hoành bằng ( -frac{b}{a} ).

+ Các bước thực hiện:

1. Cho ( x = 0 ) để tìm điểm A(0; b).
2. Cho ( y = 0 ) để tìm điểm B(-b/a; 0).
3. Vẽ đường thẳng đi qua hai điểm A và B.

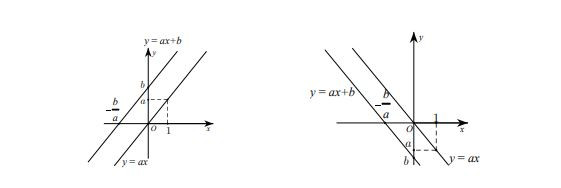Đồ thị của hàm số bậc 1 y = ax + b

+ Ví dụ

• Ví dụ 1: Vẽ đồ thị hàm số ( y = x – 3 ).

Lời giải:

• Cho ( x = 0 ) ta có ( y = -3 ) ⇒ điểm A(0; -3).
• Cho ( y = 0 ) ta có ( x = 3 ) ⇒ điểm B(3; 0).
• Đồ thị hàm số ( y = x – 3 ) là đường thẳng đi qua hai điểm A và B.

Kết luận

Hàm số bậc 1 là một chủ đề quan trọng trong toán học lớp 9, có vai trò thiết yếu trong việc phát triển khả năng tư duy và giải quyết vấn đề. Nắm vững lý thuyết và các dạng bài tập liên quan sẽ giúp học sinh tự tin hơn trong kỳ thi. Hãy truy cập vào website loigiaihay.edu.vn để tìm hiểu thêm về các kiến thức liên quan khác và ôn luyện hiệu quả!