Bài Tập Toán Lớp 8 Tập 1: Hướng Dẫn Giải Chi Tiết Về Hình Thang Cân

Trong loạt bài viết này, chúng tôi sẽ cung cấp cho các học sinh lớp 8 một hướng dẫn chi tiết về các bài tập liên quan đến hình thang cân trong chương trình Toán học. Các bài tập này không chỉ giúp củng cố kiến thức mà còn cung cấp phương pháp giải bài mạch lạc, dễ hiểu.

Hãy cùng nhau giải quyết những bài tập ở phần Bài tập và Luyện tập chung (trang 55 – 56) nhé!

I. Phân Tích Bài Tập Hình Thang Cân

Bài 3.4. Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?

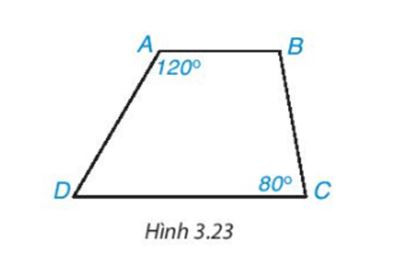Hình vẽ bài 3.4

Lời giải:

• Cách 1:
  Hình thang ABCD có AB // CD nên ta có: Góc A + góc D = 180°.

  Do đó, góc D = 180° – góc A = 180° – 120° = 60°.

  Vì góc C khác góc D (góc C = 80° ≠ góc D = 60°), nên không phải là hình thang cân.

• Cách 2:
  Giả sử hình thang ABCD là hình thang cân. Khi đó góc A = góc B = 120°; góc C = góc D = 80°.

  Suy ra góc A + góc B + góc C + góc D = 120° + 120° + 80° + 80° = 400° > 360° (không thoả mãn định lí tổng bốn góc trong một tứ giác).

  Do đó, ABCD không phải là một tứ giác, điều này mâu thuẫn với giả thiết ABCD là hình thang cân.

  Vậy ABCD không phải là hình thang cân.

Bài 3.5 (trang 55 Toán 8 Tập 1): Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

Gọi O là giao điểm của AC và BD.

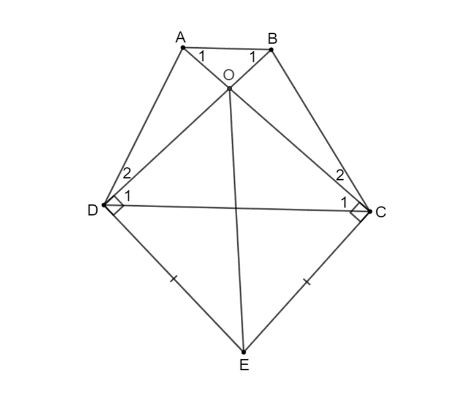Hình vẽ bài 3.5

Xét tam giác DOE và tam giác COE có:

Góc ODE = góc OCE = 90° (Vì OD ⊥ DE; OC ⊥ CE); EC = ED (giả thiết);

Cạnh OE chung.

Vì vậy tam giác DOE = tam giác COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng) (1).

Từ đó tam giác OCD cân tại O nên góc C1 = góc D1.

Vì ABCD là hình thang nên AB // CD suy ra góc A1 = góc C1; góc B1 = góc D1 (cặp góc so le trong).

Do đó góc A1 = góc B1 (vì góc C1 = góc D1).

Suy ra tam giác OAB cân tại O nên OA = OB (2).

Ta có: AC = DA + OC và BD = OB + OD (3).

Từ (1), (2) và (3) suy ra AC = BD.

Hình thang ABCD có AC = BD nên ABCD là hình thang cân.

Bài 3.6 (trang 55 Toán 8 Tập 1): Vẽ hình thang cân ABCD (AB // CD) biết đáy dài CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.

Lời giải:

Cách vẽ hình thang cân ABCD:

• Vẽ cạnh CD = 4 cm.
• Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.
• Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.
• Nối AB, AD, BC ta được hình thang cân ABCD như hình vẽ.

Hình vẽ bài 3.6

Bài 3.7 (trang 55 Toán 8 Tập 1): Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Lời giải:

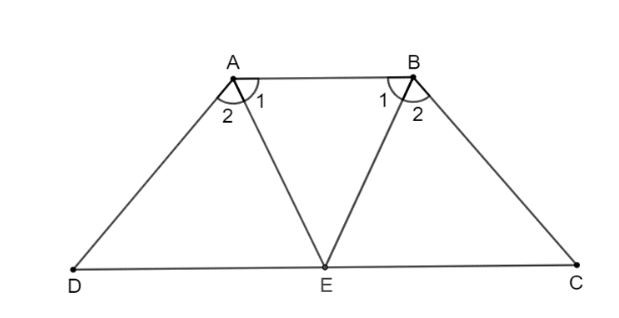Hình vẽ bài 3.7

Vì ABCD là hình thang cân nên góc DAB = góc ABC; góc C = góc D; AD = BC.

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của góc BAD và góc ABC.

Suy ra góc A1 = góc A2 = ½ góc DAB; góc B1 = góc B2 = ½ góc ABC. Mà góc DAB = góc ABC nên góc A1 = góc A2 = góc B1 = góc B2.

Xét tam giác EAB cân tại E (vì góc A1 = góc B1) nên EA = EB.

Xét tam giác ADE và tam giác BCE có:

EA = EB (chứng minh trên);

Góc A2 = góc B2 (chứng minh trên);

AD = BC (chứng minh trên).

Do đó tam giác ADE = tam giác BCE (c.g.c).

Suy ra EC = ED (hai cạnh tương ứng).

Bài 3.8 (trang 55 Toán 8 Tập 1): Hình thang cân ABCD (AB // CD) có AB = CD.

Lời giải:

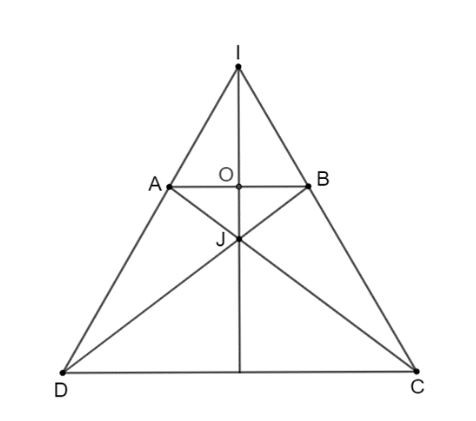Hình vẽ bài 3.8

Vì ABCD là hình thang cân nên góc BAD = góc ABC; góc ADC = góc BCD; AD = BC; AC = BD.

Xét DICD cân tại I (vì góc ADC = góc BCD) nên IC = ID.

Suy ra IC – BC = ID – AD, hay IB = IA.

Do đó I cách đều A và B nên I nằm trên đường trung trực của AB (1).

Xét tam giác ABD và tam giác BAC có:

AB là cạnh chung,

Góc BAD = góc ABC (chứng minh trên);

AD = BC (chứng minh trên).

Do đó tam giác ABD = tam giác BAC (c.g.c).

Suy ra góc ABD = góc BAC (hai góc tương ứng).

Tam giác JAB cân tại J (vì góc ABD = góc BAC) nên JA = JB.

Do đó J cách đều A và B nên J nằm trên đường trung trực của AB (2).

Từ (1) và (2) suy ra I, J cùng nằm trên đường thẳng IJ là đường trung trực của đoạn thẳng AB.

II. Phần Luyện Tập Chung Về Hình Thang Cân

Bài 3.9 (trang 56 Toán 8 Tập 1): Tứ giác ABCD trong Hình 3.25 có phải là hình thang không? Vì sao?

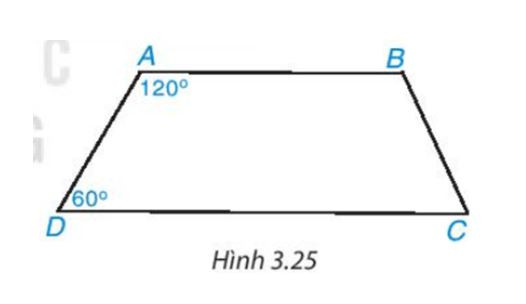Hình vẽ bài 3.9

Lời giải:

Vẽ tia Dx đi qua điểm A.

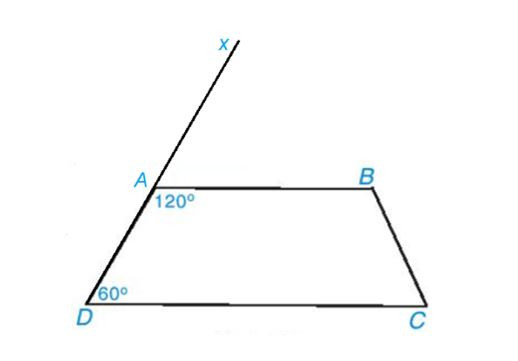Hình vẽ cho lời giải bài 3.9

Vì góc DAB và góc BAx là hai góc kề bù nên góc DAB + góc BAx = 180°.

Suy ra góc BAx = 180° – góc DAB = 180° – 120° = 60°.

Ta có góc ADC = góc BAx = 60° mà hai góc này ở vị trí đối diện nên AB // CD.

Vậy tứ giác ABCD là hình thang.

Bài 3.10 (trang 56 Toán 8 Tập 1): Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết ABD = 30°, tính số đo các góc của hình thang đó.

Lời giải:

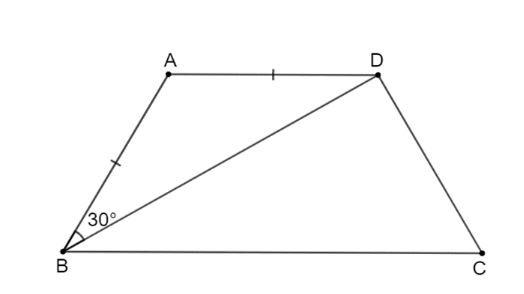Hình vẽ bài 3.10

Xét tam giác ABD cân tại A (vì AB = AD), ta có:

Góc ADB = góc ABD = 30°;

Góc A + góc ABD + góc ADB = 180° hay góc A + 30° + 30° = 180°.

Suy ra góc A = 180° – 30° – 30° = 120°.

Vì AB // CD nên góc ADB = góc CBD = 30° (hai góc so le trong).

Do đó góc ABC = góc ABD + góc CBD = 30° + 30° = 60°.

Vì tứ giác ABCD là hình thang cân nên góc C = góc ABC = 60°; góc ADC = góc A = 120°.

Vậy số đo các góc của hình thang cân ABCD là: góc A = 120°; góc ABC = 60°; góc C = 60°; góc ADC = 120°.

Bài 3.11 (trang 56 Toán 8 Tập 1): Tính số đo các góc của tứ giác ABCD trong Hình 3.26.

Hình vẽ bài 3.11

Lời giải:

Xét tam giác ABD cân tại A (vì AB = AD) ta có:

Góc ADB = góc ABD = 40°.

Góc A + góc ABD + góc ADB = 180°.

Suy ra góc A = 180° – góc ABD – góc ADB = 180° – 40° – 40° = 100°.

Ta có góc ADB + góc BDC = 120° suy ra góc BDC = 120°.

Xét tam giác BCD cân tại C (vì BC = CD) ta có:

Góc CBD = góc CDB = 80°.

Góc C + góc CBD + góc CDB = 180°.

Suy ra góc C = 180° – góc CBD – góc CDB = 180° – 80° – 80° = 20°.

Ta có: Góc ABC = góc ABD + góc CBD = 40° + 80° = 120°.

Vậy số đo các góc của tứ giác ABCD là: Góc A = 100°; góc ABC = 120°; góc C = 20°.

Bài 3.12 (trang 56 Toán 8 Tập 1): Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân.

b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.

c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều?

Lời giải:

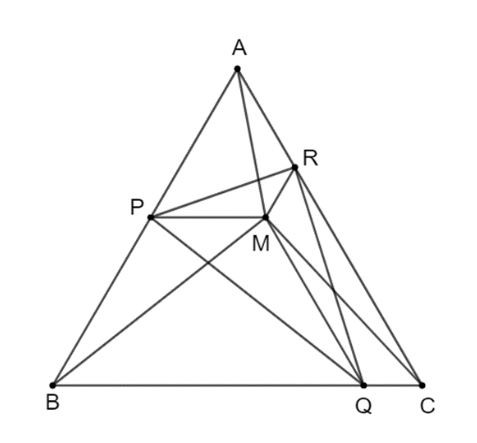Hình vẽ bài 3.12

a) Vì tam giác ABC đều nên góc BAC = góc ABC = góc ACB = 60°.

Vì PM // BC nên APM = ABC = 60° (đồng vị).

Suy ra góc APM = góc PAR (cùng bằng 60°).

Tứ giác APMR là hình thang (vì MR // AP) có góc APM = góc PAR.

b) Vì tứ giác APMR là hình thang cân nên AM = PR (1).

Chứng minh tương tự câu a, ta cũng có các tứ giác BPMQ và MQCR là hình thang cân.

Suy ra BM = PQ và MC = QR (2).

Từ (1) và (2) suy ra PR + PQ + QR = MA + MB + MC.

Mà PR + PQ + QR chính là chu vi của tam giác PQR.

Do đó chu vi tam giác PQR bằng tổng độ dài MA + MB + MC (đpcm).

c) Để tam giác PQR là tam giác đều thì PR = PQ = QR. Suy ra MA = MB = MC.

Khi đó điểm M cách đều ba đỉnh A, B, C của tam giác ABC.

Vì vậy, M là giao điểm của ba đường trung trực (đường thẳng đi qua trung điểm của các cạnh và vuông góc với các cạnh đó).

Hi vọng rằng phần giải bài tập Toán lớp 8 tập 1 bài 11 trang 51: Hình thang cân ở trên của chúng tôi sẽ giúp các em hiểu rõ hơn về cách áp dụng kiến thức vào giải các bài toán về hình thang cân, đồng thời cũng củng cố thêm sự tự tin trong quá trình học tập môn Toán.

Hãy tiếp tục ôn luyện và thực hành thường xuyên để nắm vững các kiến thức cơ bản, từ đó chuẩn bị tốt nhất cho các kỳ thi sắp tới.

Chúc các em học tập hiệu quả và đạt được kết quả cao!

Các dạng toán và lý thuyết ở trên đều có sẵn trong cuốn Làm chủ kiến thức Toán bằng sơ đồ tư duy lớp 8 – Tập 1. Các em nên mua cuốn sách này để hỗ trợ cho việc học Toán của mình nhé! Ngoài ra TKbooks cũng có đủ bộ sách tham khảo lớp 8 của môn Ngữ Văn và Tiếng Anh với nội dung bám sát chương trình học mới nhất.

Link để thử sách: https://drive.google.com/file/d/1TsmoDs83uAwQu0FqU6ikrzFtEBDMH2Kq/view

TKbooks tự hào là nhà xuất bản sách tham khảo lớp 8 hàng đầu tại Việt Nam!

TKbooks.vn