Cung và góc lượng giác là những khái niệm cơ bản nhưng vô cùng quan trọng trong chương trình Toán học THPT. Kiến thức này không chỉ xuất hiện trong các bài toán mà còn chiếm khoảng 10% trong đề thi THPT Quốc Gia, do đó, việc nắm vững phần này là extremely cần thiết để các em có thể đạt điểm cao trong kỳ thi.
Trong bài viết này, chúng ta sẽ đi sâu vào từng khía cạnh của cung và góc lượng giác. Hãy cùng khám phá những kiến thức này để chuẩn bị cho các kỳ thi sắp tới nhé!
I. Khái Niệm Cung Và Góc Lượng Giác
1. Đường Tròn Định Hướng và Cung Lượng Giác
Đường tròn định hướng là tập hợp các điểm, nơi mỗi điểm có thể được xác định bằng góc từ một điểm cố định (gọi là điểm O) tới điểm đó. Độ dài của cung lượng giác giữa hai điểm A và B trên đường tròn được ký hiệu là ( overset{frown}{AB} ).
 Cung Lượng Giác
Cung Lượng Giác
Khi đưa ra hai điểm A và B trên đường tròn, ta có thể xác định vô số cung lượng giác. Mỗi cung được đánh dấu bằng ( overset{frown}{AB} ).
2. Góc Lượng Giác
Góc lượng giác được xác định qua tia OM quay quanh điểm O. Tia OM tạo nên một góc giữa tia đầu OC và tia cuôi OD. Ký hiệu của góc lượng giác này là ((OC, OD)).
Khi tia OM quay từ vị trí OC sang OD, nó tạo ra một góc lượng giác mà chúng ta có thể đo bằng độ hoặc radian.
3. Đường Tròn Lượng Giác
Trong mặt phẳng tọa độ Oxy, đường tròn lượng giác với tâm O và bán kính R=1 được sử dụng để mô hình hóa các hàm lượng giác. Đường tròn này cắt hai trục tọa độ tại các điểm có tọa độ cụ thể, giúp xác định các giá trị lên tới các cung lượng giác.
Đường Tròn Lượng Giác
II. Số Đo Cung và Góc Lượng Giác
1. Đơn Vị Radian
Trên đường tròn, một cung có độ dài bằng bán kính được gọi là 1 radian. Nếu một cung có độ dài bằng ( pi R ), thì nó tương ứng với(( pi ) rad).
Quan Hệ Giữa Độ Và Radian
2. Giá Trị Đo Của Một Cung Lượng Giác
Số đo của một cung lượng giác được ký hiệu là ( S_{overset{frown}{AM}} ), trong đó A là điểm đầu và M là điểm cuối của cung.
Formulas:
( S_{overset{frown}{AM}} = alpha + k cdot 2pi, text{ trong đó } k in Z )
3. Giá Trị Đo Của Một Góc Lượng Giác
Số đo của góc lượng giác ((OA, OC)) được xác định bằng cung lượng giác tương ứng.
4. Biểu Diễn Cung Lượng Giác Trên Đường Tròn Lượng Giác
Chọn điểm A(1;0) làm điểm đầu của tất cả các cung lượng giác. Để biểu diễn cung lượng giác có số đo ( alpha ) trên đường tròn lượng giác, chúng ta cần xác định điểm M cuối của cung này.
III. Giá Trị Lượng Giác Của Một Cung
1. Giá Trị Lượng Giác của Cung ( alpha )
Giá trị lượng giác phổ biến (sin alpha), (cos alpha), (tan alpha), (cot alpha) là các giá trị quan trọng trong các bài toán liên quan.
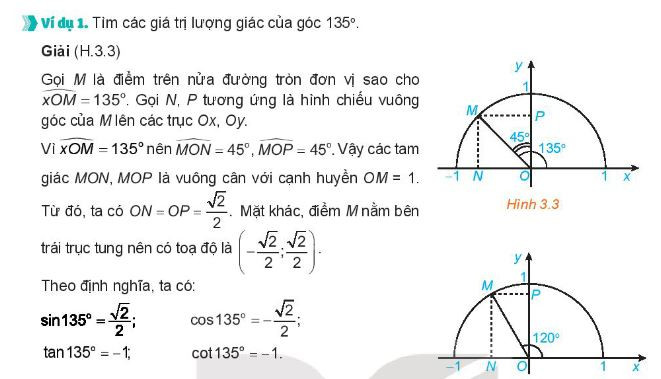 Giá Trị Lượng Giác
Giá Trị Lượng Giác
Các học sinh cũng nên lưu ý những giá trị đặc biệt của các cung lượng giác, như 0, ( frac{pi}{6} ), ( frac{pi}{4} ), ( frac{pi}{3} ) và ( frac{pi}{2} ).
2. Ý Nghĩa Hình Học Của Tang, Cotang
Tang và cotang được định nghĩa từ các góc tương ứng với tiệm cận.
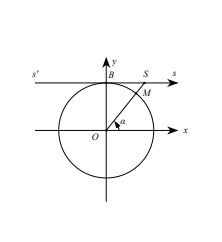 Ý Nghĩa Hình Học của Tang Cotang
Ý Nghĩa Hình Học của Tang Cotang
IV. Công Thức Lượng Giác
1. Công Thức Cộng
Công thức cộng đồng điều kiện lượng giác cung cấp cách tính giá trị nó cho các góc khác nhau.
( cos(a pm b) = cos a cos b mp sin a sin b )
( sin(a pm b) = sin a cos b pm cos a sin b )
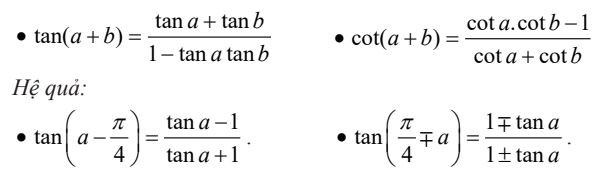 Công Thức Cộng Lượng Giác
Công Thức Cộng Lượng Giác
2. Công Thức Nhân Đôi
Các công thức nhân đôi cung cấp thêm thông tin về tính chất của các giá trị góc.
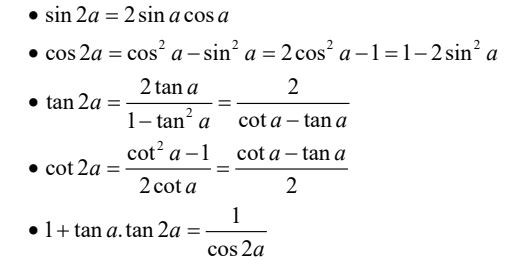 Công Thức Nhân Đôi Lượng Giác
Công Thức Nhân Đôi Lượng Giác
V. Một Số Bài Tập Để Củng Cố Kiến Thức
Khi đã cắm rễ các kiến thức này, các em hãy làm việc với một số dạng bài tập để thực hành và củng cố hiểu biết của mình.
 Bài Tập Tìm Giá Trị Lượng Giác
Bài Tập Tìm Giá Trị Lượng Giác
VI. Cách Tính Giá Trị Lượng Giác Bằng Máy Tính
Máy tính cung cấp một công cụ hữu dụng để tính nhanh các giá trị lượng giác.
 Cách Tính Giá Trị Lượng Giác Bằng Máy Tính
Cách Tính Giá Trị Lượng Giác Bằng Máy Tính
Hãy tham khảo thêm tài liệu ở trang loigiaihay.edu.vn để biết thêm nhiều kiến thức bổ ích khác trong môn Toán học!
Để lại một bình luận