Trong chương trình học toán từ lớp 7 đến lớp 9, việc chứng minh ba điểm thẳng hàng là một kỹ năng quan trọng. Trong bài viết này, chúng tôi sẽ hướng dẫn các em ba phương pháp chứng minh ba điểm A, B, C thẳng hàng, từ cơ bản đến nâng cao. Hãy cùng tìm hiểu!
I. Cách Chứng Minh Ba Điểm Thẳng Hàng Lớp 7
1. Sử Dụng Góc:
Nguyên lý:
Nếu ba điểm A, B, C nằm trên một đường thẳng, thì góc giữa các đoạn thẳng AB và BC bằng 180 độ. Tổng các góc trong tam giác ABC bằng 0 độ vì tam giác đó không tồn tại (các điểm nằm trên cùng một đường thẳng).
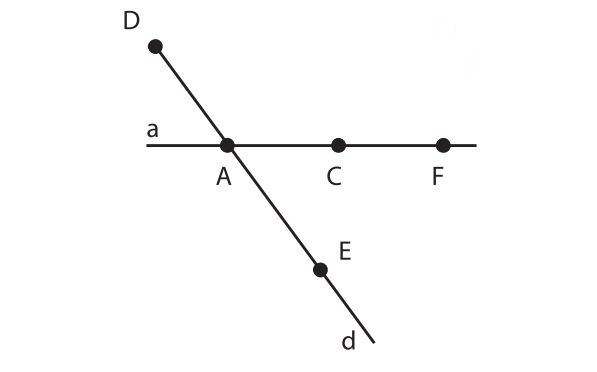 Chứng minh ba điểm thẳng hàng bằng phương pháp sử dụng góc
Chứng minh ba điểm thẳng hàng bằng phương pháp sử dụng góc
Phương pháp chứng minh:
- Cách 1: Sử Dụng góc kề bù
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Chứng minh rằng hai góc tạo bởi các đoạn thẳng AB và BC là góc kề bù (nếu ∠ABC + ∠CBA = 180 độ thì ba điểm thẳng hàng).
- Cách 2: Sử Dụng góc bẹt
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Tính góc tạo bởi hai đoạn thẳng AB và BC. Nếu góc ∠ABC = 180 độ thì ba điểm thẳng hàng.
- Cách 3: Tổng góc trong tam giác bằng 0 độ
- Bước 1: Giả sử ba điểm A, B, C không thẳng hàng.
- Bước 2: Tính tổng ba góc ∠ABC, ∠BCA, và ∠CAB. Nếu tổng bằng 0 độ thì tam giác không tồn tại, tức ba điểm thẳng hàng.
2. Sử Dụng Tính Đường Quy:
Nguyên lý:
Ba điểm A, B, C thẳng hàng nếu chúng nằm trên cùng một đường thẳng duy nhất. Điều này có nghĩa là:
- Chúng đồng quy tại một đường thẳng.
- Mỗi đoạn thẳng nối giữa hai điểm bất kỳ trong ba điểm đều nằm trên cùng một đường thẳng.
Phương pháp chứng minh bằng tính đường quy:
- Cách 1: Sử Dụng đường thẳng chứa hai điểm.
- Bước 1: Chọn hai điểm trong ba điểm A, B, C (ví dụ A và B).
- Bước 2: Xác định đường thẳng d đi qua hai điểm A và B.
- Bước 3: Chứng minh rằng điểm thứ ba (C) cũng nằm trên đường thẳng d.
3. Sử Dụng Tiên Đề Euclid:
- Cách 1: Dùng tính chất đường trung trực
- Bước 1: Xác định ba điểm A, B, C.
- Bước 2: Chứng minh rằng cả ba điểm cùng cách đều hai đầu mút của một đoạn thẳng PQ nào đó.
II. Cách Chứng Minh Ba Điểm Thẳng Hàng Lớp 8
1. Sử Dụng Định Lý Thales:
Nguyên lý:
Khi xét ba điểm A, B, C, nếu tỷ lệ các đoạn thẳng bằng nhau AB/BC=AD/DC (nếu D là điểm bất kỳ trên một đường thẳng song song) thì ba điểm A, B, C thẳng hàng.
Phương pháp chứng minh:
- Bước 1: Xác định ba điểm cần chứng minh.
- Bước 2: Áp dụng định lý Thales để tạo một đường thẳng song song với đoạn thẳng AC và xác định điểm D. Theo định lý Thales, nếu tỷ lệ AB/BC=AD/DC thì ba điểm A, B, C sẽ thẳng hàng.
2. Phương Pháp Tọa Độ:
Nguyên lý:
Ba điểm A(x1, y1), B(x2, y2), C(x3, y3) thẳng hàng nếu:
[
frac{y2 – y1}{x2 – x1} = frac{y3 – y2}{x3 – x2}
]
Hoặc:
[
(y2 – y1)(x3 – x2) = (y3 – y2)(x2 – x1)
]
Phương pháp chứng minh:
- Bước 1: Đặt tọa độ của ba điểm.
- Bước 2: Tính hệ số góc giữa các cặp điểm.
- Bước 3: So sánh hệ số góc. Nếu chúng bằng nhau thì ba điểm A, B, C thẳng hàng.
3. Dựa Trên Tính Chất Đối Đẳng:
Nguyên lý:
Khi hai tam giác đồng dạng, các cạnh tương ứng tỷ lệ với nhau. Sử dụng tính chất đồng dạng để chứng minh ba điểm thẳng hàng.
Phương pháp chứng minh:
- Bước 1: Xác định hai tam giác đồng dạng.
- Bước 2: Sử dụng tính chất đồng dạng để chứng minh tỷ lệ giữa các đoạn thẳng.
III. Cách Chứng Minh Ba Điểm Thẳng Hàng Lớp 9
1. Phương Pháp Vecto:
Nguyên lý:
Ba điểm A, B, C thẳng hàng khi vecto AB và AC cùng phương, tức là vecto AB = k. vecto AC với k là số thực.
Phương pháp chứng minh:
- Bước 1: Biểu diễn các vecto.
- Bước 2: Kiểm tra điều kiện cùng phương. Nếu tích chéo giữa hai vecto bằng 0 thì A, B, C thẳng hàng.
2. Sử Dụng Phương Trình Đường Thẳng:
Nguyên lý:
Ba điểm A(x1, y1), B(x2, y2), C(x3, y3) thẳng hàng nếu tọa độ của điểm C thỏa mãn phương trình đường thẳng đi qua hai điểm A và B.
Phương pháp chứng minh:
- Bước 1: Lập phương trình đường thẳng đi qua A và B.
- Bước 2: Thay tọa độ của điểm C vào phương trình xác định. Nếu kết quả bằng 0, thì ba điểm thẳng hàng.
3. Sử Dụng Các Định Lý Nâng Cao (Menelaus hoặc Ceva):
Sử Dụng Định Lý Menelaus:
- Phát biểu: Cho tam giác ABC, đường thẳng bất kỳ cắt các cạnh BC, CA và AB tại các điểm D, E, F tương ứng thì ba điểm D, E, F thẳng hàng nếu BD/DC x CE/EA x AF/FB=1.
Kết Luận
Hi vọng rằng những cách chứng minh ba điểm thẳng hàng mà chúng tôi đã chia sẻ sẽ giúp các em củng cố kiến thức môn Toán, đồng thời chuẩn bị tốt cho các kỳ thi và bài kiểm tra. Các em cũng đừng quên tham khảo tài liệu và sách tham khảo chất lượng để học tốt hơn nhé!
Hãy truy cập loigiaihay.edu.vn để tìm hiểu thêm về phong cách học và cách giải bài tập trong chương trình học!
Để lại một bình luận