Trong chương trình Toán học THPT, kiến thức về đường thẳng và mặt phẳng trong không gian là một phần rất quan trọng. Kiến thức này xuất hiện trong khoảng 10% các bài toán và câu hỏi trong đề thi THPT Quốc Gia. Điều này đòi hỏi các em học sinh cần nắm vững phần kiến thức này để đạt được điểm số cao.
Dưới đây là tổng hợp kiến thức về đường thẳng và mặt phẳng trong không gian. Các em hãy lưu ý và ôn luyện thường xuyên để nắm chắc kiến thức nhé!
I. Giới thiệu về Đường thẳng và Mặt phẳng
1. Khái niệm cơ bản về đường thẳng và mặt phẳng
Trong không gian, đường thẳng và mặt phẳng là hai đối tượng cơ bản.
a) Đường thẳng và điều kiện:
- Một điểm A thuộc đường thẳng d. Kí hiệu A ∈ d.
- Một điểm A không thuộc đường thẳng d. Kí hiệu A ∉ d.
b) Mặt phẳng và điều kiện:
- Một điểm A thuộc mặt phẳng (P). Kí hiệu A ∈ (P).
- Một điểm A không thuộc mặt phẳng (P). Kí hiệu A ∉ (P).
2. Các tính chất của hình học không gian
- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
- Tính chất 3: Tồn tại một bộ điểm không cùng nằm trên một mặt phẳng.
- Tính chất 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
- Tính chất 5: Trong mỗi mặt phẳng, các kết luận đã biết của hình học phẳng đều đúng.
Định lý: Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì điểm của đường thẳng đó đều thuộc mặt phẳng đó.
 Ví dụ về sự tồn tại của đường thẳng và mặt phẳng
Ví dụ về sự tồn tại của đường thẳng và mặt phẳng
3. Điều kiện xác định một mặt phẳng
Có bốn cách xác định trong một mặt phẳng:
- Một mặt phẳng được xác định nếu biết nó đi qua ba điểm A, B, C không thẳng hàng, kí hiệu (A, B, C).
- Một mặt phẳng được xác định nếu biết nó đi qua một đường thẳng d và một điểm A không thuộc d, kí hiệu (A, d).
- Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b cắt nhau, kí hiệu (a, b).
- Một mặt phẳng được xác định nếu biết nó đi qua hai đường thẳng a, b song song, kí hiệu (a, b).
4. Hình chop và tứ diện
Định nghĩa: Cho một đa giác A1A2,…An và cho điểm S nằm ngoài mặt phẳng chứa đa giác đó. Nối S với các đỉnh A1A2,…An ta được n mặt tam giác SA1A2, SA2A3, … SAn-1An.
Hình gồm n tam giác đó và đa giác A1A2A3…An được gọi là hình chop S.A1A2A3…An.
Trong đó:
- Điểm S gọi là đỉnh của hình chop.
- Đa giác A1A2A3…An gọi là mặt đáy của hình chop.
- Các đoạn thẳng A1A2, A2A3, …, An-1An gọi là các cạnh bên của hình chop.
- Các mặt tam giác SA1A2, SA2A3, …, SAn-1An gọi là các mặt bên của hình chop.
Nếu đáy của hình chop là một miền tam giác, tứ giác, ngũ giác thì hình chop tương ứng gọi là hình chop tam giác, hình chop tứ giác, hình chop ngũ giác.
 Hình chop và tứ diện
Hình chop và tứ diện
II. Hai Đường thẳng chéo nhau và Hai Đường thẳng song song
1. Vị trí tương đối của hai đường thẳng phân biệt
Cho hai đường thẳng a và b. Căn cứ vào sự đồng phẳng và số điểm chung của hai đường thẳng ta có bốn trường hợp sau:
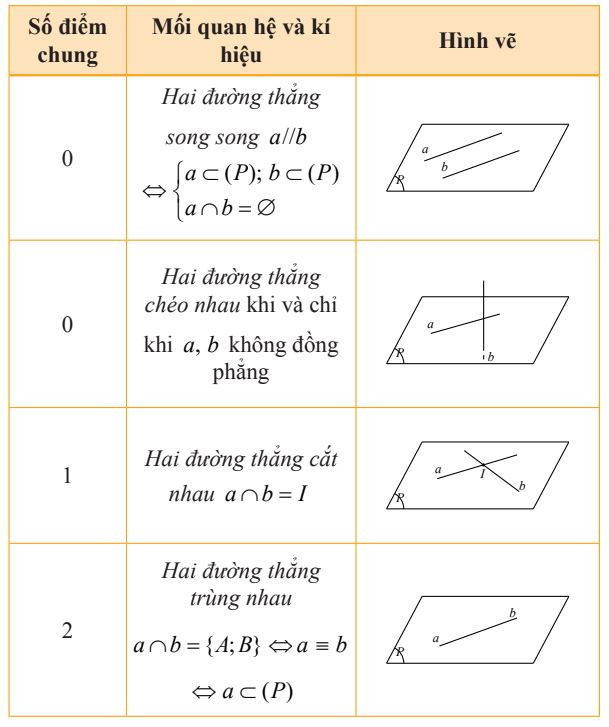 Vị trí tương đối của hai đường thẳng
Vị trí tương đối của hai đường thẳng
2. Hai đường thẳng song song
- Tính chất 1: Trong không gian, qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó.
- Tính chất 2: Hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì song song với nhau.
Định lý: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó hoặc đồng quy hoặc đôi một song song.
 Ví dụ về vị trí tương đối của hai đường thẳng
Ví dụ về vị trí tương đối của hai đường thẳng
III. Đường thẳng và Mặt phẳng
1. Vị trí tương đối của đường thẳng và mặt phẳng
Cho đường thẳng a và mặt phẳng (P). Căn cứ vào số điểm chung của đường thẳng và mặt phẳng ta có ba trường hợp sau:
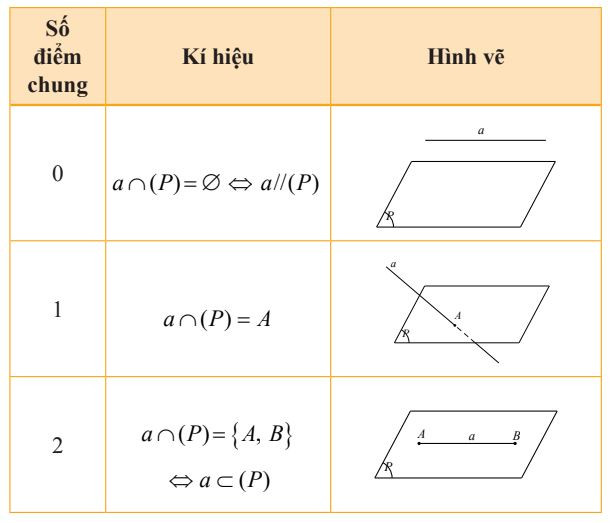 Vị trí tương đối của đường thẳng và mặt phẳng
Vị trí tương đối của đường thẳng và mặt phẳng
2. Điều kiện để một đường thẳng song song với một mặt phẳng
Định lý 1: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nào đó trong (P) thì a song song với (P).
3. Tính chất
Định lý 2: Nếu đường thẳng a song song với mặt phẳng (P) thì mọi mặt phẳng (Q) chứa a cắt (P) thì sẽ cắt (Q) theo một giao tuyến song song với a.
IV. Hai Mặt phẳng song song
1. Vị trí tương đối của hai mặt phẳng phân biệt
Cho hai mặt phẳng (P) và (Q). Căn cứ vào số đường thẳng chung của hai mặt phẳng ta có ba trường hợp sau:
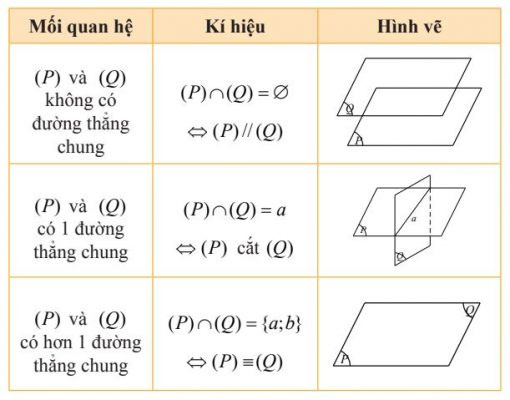 Vị trí tương đối của hai mặt phẳng phân biệt
Vị trí tương đối của hai mặt phẳng phân biệt
2. Điều kiện để hai mặt phẳng song song
Định lý 1: Nếu mặt phẳng (P) chứa hai đường thẳng a, b cùng song song với một mặt phẳng (Q) thì (P) song song với (Q).
3. Tính chất
Tính chất 1: Qua một điểm nằm ngoài một mặt phẳng, có một và chỉ một mặt phẳng song song với mặt phẳng đó.
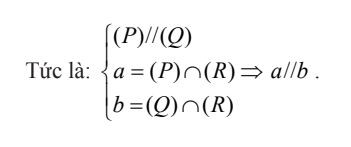 Tính chất của hai mặt phẳng song song
Tính chất của hai mặt phẳng song song
4. Hình lăng trụ và hình hộp
Định nghĩa hình lăng trụ: Hình lăng trụ là một hình đa diện có hai mặt nằm trong hai mặt phẳng song song gọi là hai đáy và tất cả các cạnh không thuộc hai đáy đều song song với nhau.
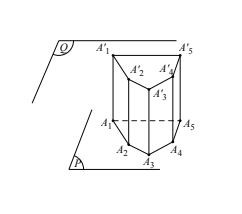 Hình lăng trụ
Hình lăng trụ
Định nghĩa hình hộp: Hình lăng trụ có đáy là hình bình hành gọi là hình hộp.
V. Bài tập về đường thẳng và mặt phẳng trong không gian
Dưới đây là một số dạng toán cơ bản về đường thẳng và mặt phẳng trong không gian để các em luyện tập:
 Bài tập về đường thẳng và mặt phẳng trong không gian
Bài tập về đường thẳng và mặt phẳng trong không gian
Các dạng toán khác về đường thẳng và mặt phẳng trong không gian được ghi chú và diễn giải rất đầy đủ trong cuốn Sổ tay Toán học cấp 3 All in one của Tkbooks. Các bạn hãy mua ngay cuốn sách này để ôn luyện các dạng toán này tốt hơn nhé!
Tkbooks tự hào là nhà xuất bản sách tham khảo cho học sinh cấp 3 hàng đầu tại Việt Nam.
Tkbooks.vn
Để lại một bình luận