Các công thức lũy thừa lớp 6 và bài tập áp dụng

Nội dung bài viết này sẽ giới thiệu các công thức lũy thừa lớp 6 dưới dạng sơ đồ tư duy, kèm theo bài tập thực hành được chia thành các dạng toán với lời giải chi tiết giúp học sinh củng cố kiến thức một cách hiệu quả.

I. Các công thức lũy thừa

1. Lũy thừa với số tự nhiên

( a^n = a times a times … times a ) (n lần a, với n là số tự nhiên).
Ví dụ: ( 2^3 = 2 times 2 times 2 = 8 ).

2. Nhân hai lũy thừa cùng cơ số

( a^m times a^n = a^{m+n} ).
Ví dụ: ( 2^3 times 2^4 = 2^{3+4} = 2^7 = 128 ).

3. Chia hai lũy thừa cùng cơ số

( frac{a^m}{a^n} = a^{m-n} ) (a ≠ 0).
Ví dụ: ( frac{2^5}{2^2} = 2^{5-2} = 2^3 = 8 ).

4. Lũy thừa của một lũy thừa

( (a^m)^n = a^{m times n} ).
Ví dụ: ( (2^3)^2 = 2^{3 times 2} = 2^6 = 64 ).

5. Lũy thừa của một tích

( (a times b)^n = a^n times b^n ).
Ví dụ: ( (2 times 3)^2 = 2^2 times 3^2 = 4 times 9 = 36 ).

6. Lũy thừa của một thương

( left( frac{a}{b} right)^n = frac{a^n}{b^n} ) (b ≠ 0).
Ví dụ: ( left( frac{2}{3} right)^2 = frac{2^2}{3^2} = frac{4}{9} ).

7. Lũy thừa với số 0

( a^0 = 1 ) (a ≠ 0).
Ví dụ: ( 5^0 = 1 ).

8. Lũy thừa với số 1

( a^1 = a ).
Ví dụ: ( 7^1 = 7 ).

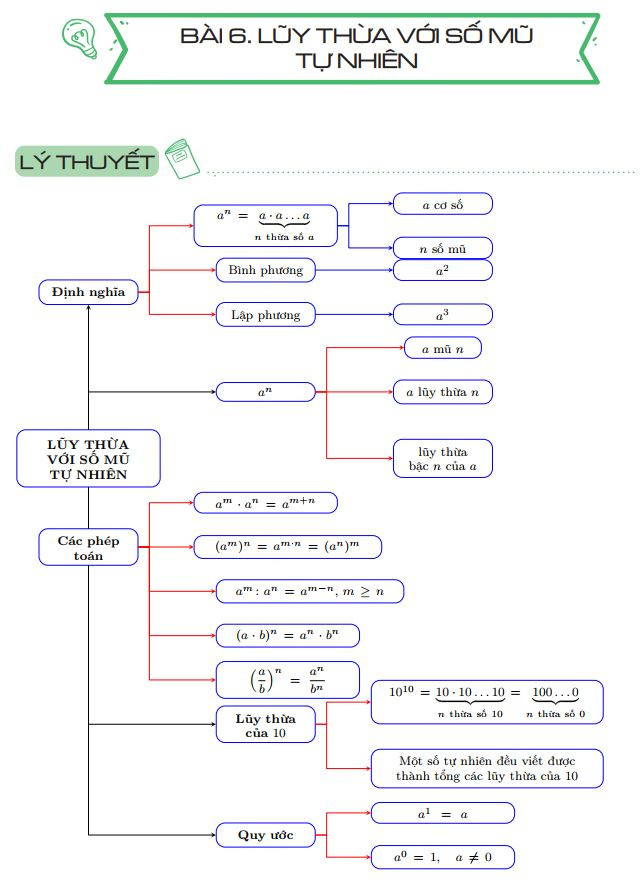Các công thức lũy thừa lớp 6 dưới dạng sơ đồ tư duy

II. Các dạng toán về lũy thừa lớp 6 kèm lời giải chi tiết

Dạng 1: Dùng lũy thừa để viết gọn các tích nhiều số giống nhau

1. Phương pháp

Biến đổi để xuất hiện các lũy thừa giống nhau.
Áp dụng quy tắc: ( a times a times … times a = a^n ) (n là số tự nhiên).

2. Các ví dụ

Ví dụ 1:

• Viết gọn các tích sau bằng cách dùng lũy thừa:
  • a) ( 7 times 7 times 7 times 7 );
  • b) ( 3 times 5 times 15 times 15 );
  • c) ( 2 times 2 times 5 times 2 times 5 );
  • d) ( 1000 times 10 times 10 );
  • e) ( a times a times a times b times b times b times b );
  • g) ( x times x times x + y times y times y ).

Hướng dẫn giải

• a) ( 7 times 7 times 7 times 7 = 7^4 ).
• b) ( 3 times 5 times 15 times 15 = 15 times 15 times 15 = 15^3 ).
• c) ( 2 times 2 times 5 times 2 times 5 = 2^3 times 5^2 ).
• d) ( 1000 times 10 times 10 = 10 times 10 times 10 times 10 = 10^5 ).
• e) ( a times a times a times b times b times b times b = a^3 times b^4 ).
• g) ( x times x times x + y times y times y = x^3 + y^3 ).

Dạng 2: Nhân, chia hai lũy thừa cùng cơ số

1. Phương pháp

Sử dụng công thức ( a^m times a^n = a^{m+n} ) và ( frac{a^m}{a^n} = a^{m-n} ).

2. Ví dụ

Ví dụ: Viết kết quả phép tính sau dưới dạng lũy thừa:

• a) ( 16^3 times 24 );
• b) ( a^4 times a times a^2 );
• c) ( frac{a^4}{a} (a ≠ 0) );
• d) ( frac{415}{45} );
• e) ( frac{46}{46} );
• g) ( frac{98}{32} ).

Hướng dẫn giải

• a) ( 16^3 times 24 = 16^{3+1} = 16^4 ).
• b) ( a^4 times a times a^2 = a^{4+1+2} = a^7 ).
• c) ( frac{a^4}{a} = a^{4-1} = a^3 ).
• d) ( frac{415}{45} = 415 – 5 = 410 ).
• e) ( frac{46}{46} = 1 ).
• g) ( frac{98}{32} = 98 – 1 = 97 ).

Dạng 3: Viết một số dưới dạng tổng các lũy thừa của 10

1. Phương pháp

Viết ( abcd ) thành ( a times 10^3 + b times 10^2 + c times 10^1 + d times 10^0 ).

2. Ví dụ

Viết số sau dưới dạng tổng các lũy thừa của 10:

• a) ( 234 );
• b) ( 2056 );
• c) ( 2670 ).

Hướng dẫn giải

• a) ( 234 = 2 times 10^2 + 3 times 10^1 + 4 times 10^0 ).
• b) ( 2056 = 2 times 10^3 + 0 times 10^2 + 5 times 10^1 + 6 times 10^0 ).
• c) ( 2670 = 2 times 10^3 + 6 times 10^2 + 7 times 10^1 + 0 times 10^0 ).

Dạng 4: Tìm số mũ hoặc cơ số của một lũy thừa

1. Phương pháp

Đưa hai lũy thừa bằng nhau:

• Trường hợp số mũ bằng nhau, thì ( a = b ).
• Trường hợp cơ số bằng nhau, thì nếu ( a neq 0, a neq 1 ) thì ( m = n ).

2. Ví dụ

Ví dụ 1: Tìm số tự nhiên n, biết:

• a) ( 2^n = 8 );
• b) ( 7^n = 49 );
• c) ( 4^n = 64 );
• d) ( 5^n = 625 ).

Hướng dẫn giải

• a) ( 2^n = 8 ) → ( 2^n = 2^3 ) → ( n = 3 ).
• b) ( 7^n = 49 ) → ( 7^n = 7^2 ) → ( n = 2 ).
• c) ( 4^n = 64 ) → ( 4^n = 4^3 ) → ( n = 3 ).
• d) ( 5^n = 625 ) → ( 5^n = 5^4 ) → ( n = 4 ).

Hy vọng các công thức lũy thừa lớp 6 dưới dạng sơ đồ tư duy kèm bài tập và lời giải chi tiết trên đây sẽ giúp các em học sinh có cái nhìn toàn diện hơn về các dạng toán lũy thừa cũng như có thêm tài liệu tham khảo hữu ích để rèn luyện.

Hãy tiếp tục ôn tập và thực hành nhiều hơn để là chủ kiến thức và đạt được kết quả tốt trong học tập! Ghé thăm loigiaihay.edu.vn để tìm hiểu thêm về các kiến thức toán học và tài liệu tham khảo chất lượng nhé!