Trong bài viết này, chúng ta sẽ cùng nhau khám phá và làm rõ các dạng bài tập liên quan đến tam giác đều dành cho học sinh lớp 8. Bài viết không chỉ hướng dẫn giải bài tập một cách mạch lạc và chi tiết, mà còn giúp các bạn hình dung rõ hơn qua việc áp dụng lý thuyết vào thực hành. Cùng theo dõi nhé!
Dạng 1: Chứng Minh Hai Tam Giác Đều Đang
1. Phương Pháp Giải
Dựa vào định nghĩa, tính chất hoặc định lý để chứng minh các tam giác đều đang.
2. Các Ví Dụ
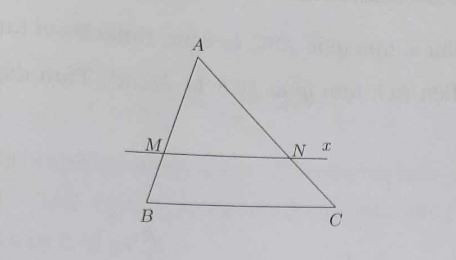
Ví Dụ 1: Tìm các cặp tam giác đều đang trong các tam giác dưới đây:
-
Giải: Xét tam giác ABC và DEF, ta có:
[
frac{AB}{DE} = frac{2}{4} = frac{1}{2}; quad frac{AC}{EF} = frac{3}{6} = frac{1}{2}; quad frac{BC}{DF} = frac{4}{8} = frac{1}{2}.
]Suy ra ( frac{AB}{DE} = frac{AC}{EF} = frac{BC}{DF} = frac{1}{2} ).
Vậy ( triangle ABC sim triangle DEF ).
* Hình vẽHình vẽ*
Hình vẽHình vẽ*
Dạng 2: Tính Độ Dài Cạnh, Tỷ Số Đang Thông Qua Các Tam Giác Đều
1. Phương Pháp Giải
- Sử dụng định nghĩa và tính chất hai tam giác bằng nhau.
- Áp dụng tính chất dầy tỷ số bằng nhau.
2. Các Ví Dụ
Ví Dụ 1: Tam giác ABC đều đang tam giác DEF theo tỷ số đang là ( frac{2}{3} ).
- a) Biết chu vi tam giác ABC là 8cm, tính chu vi tam giác DEF.
- b) Biết diện tích tam giác DEF là 27cm². Tính diện tích tam giác ABC.
+ Giải:
-
a) Gọi ( P ) là chu vi. Tam giác ABC đều đang với tam giác DEF theo tỷ số đang là ( frac{2}{3} ).
[
text{Chu vi tam giác } ABC/text{ Chu vi tam giác } DEF = frac{2}{3}.
]Từ đó chu vi tam giác DEF = ( frac{3}{2} times text{Chu vi tam giác } ABC = frac{3}{2} times 8 = 12 text{ cm}. )
-
b) Tam giác DEK đều đang với tam giác ABH (do góc DEK = góc ABH, góc DKE = góc AHB).
Suy ra:
[
text{Diện tích tam giác } ABC/text{Diện tích tam giác } DEF = left( frac{2}{3} right)^2 = frac{4}{9}.
]Vậy:
[
text{Diện tích tam giác } ABC = frac{4}{9} times 27 = 12 text{ cm}^2.
]
Dạng 3: Nhận Biết Hai Tam Giác Đang Theo Trường Hợp CCC và Chứng Minh Tính Chất Hình Học
+ Phương Pháp Giải
Để chứng minh hai tam giác đang, ta lập tỷ số các cạnh tương ứng của hai tam giác và chứng minh chúng bằng nhau.
+ Các Ví Dụ
Ví Dụ 1: Tam giác ABC có ( BC = a, AC = b, AB = c ) và ( a^2 = bc ). Chứng minh rằng tam giác ABC đang với tam giác có độ dài các cạnh bằng độ dài ba đường cao của tam giác ABC.
+ Giải:
Gọi độ dài ba đường cao kẻ từ A, B, C của ( triangle ABC ) lần lượt là ( h_a, h_b, h_c ).
Ta có:
[
frac{1}{2}a.h_a = frac{1}{2}b.h_b = frac{1}{2}c.h_c quad (text{cùng là diện tích } triangle ABC).
]
Suy ra:
[
(h_a / a) = (h_b / b) = (h_c / c).
]
Xét ( triangle ABC ) và ( triangle DEF ) ta có:
[
frac{AB}{DE} = frac{AC}{DF} = frac{BC}{EF} quad text{(vì } h_a/a = h_b/c = h_c/b text{)}.
]
Vậy ( triangle ABC sim triangle DEF ).
Kết Luận
Trong bài viết này, chúng ta đã cùng nhau tìm hiểu các dạng bài tập về tam giác đều trong chương trình toán lớp 8. Việc nắm vững lý thuyết và thực hành sẽ giúp các em tự tin hơn trong học tập và chuẩn bị cho các kỳ thi sắp tới.
Để có thêm tài liệu và hướng dẫn học tập hữu ích, hãy truy cập loigiaihay.edu.vn để tìm kiếm thêm thông tin và bài tập nhằm nâng cao kiến thức toán học của bạn!
Để lại một bình luận